Адаптивный линейный элемент
Материал из MachineLearning.
| Строка 13: | Строка 13: | ||
'''a(x) =(w,x) ''', где '''(w,x)''' - скалярное произведение, '''w''' и '''x''' - векторы весов и импульсов-признаков соответственно. | '''a(x) =(w,x) ''', где '''(w,x)''' - скалярное произведение, '''w''' и '''x''' - векторы весов и импульсов-признаков соответственно. | ||
| - | === | + | === Обучение ADALINE === |
| - | Пусть дана обучающая выборка: множество входных значений '''X''' и множество выходящих значений '''Y''', такие что каждому входу '''x<sub>j</sub>''' соответствует '''y<sub>j</sub>''' - выход, '''j = 1.. | + | Пусть дана обучающая выборка: множество входных значений '''X''' и множество выходящих значений '''Y''', такие что каждому входу '''x<sub>j</sub>''' соответствует '''y<sub>j</sub>''' - выход, '''j = 1..m'''. Необходимо по этим данным построить ADALINE, которая допускает наименьшее количество ошибок на этой обучающей выборке. |
Обучение ADALINE заключается в подборе "наилучших" значений вектора весов '''w'''. Какие значение весов лучше определяет | Обучение ADALINE заключается в подборе "наилучших" значений вектора весов '''w'''. Какие значение весов лучше определяет | ||
| - | ''функционал потерь''.В ADALINE используется функционал, предложенный Видроу и Хоффом, '''L(a,x) = (a - y)<sup>2</sup>'''. | + | ''функционал потерь''.В ADALINE используется функционал, предложенный Видроу и Хоффом, '''L(a,x) = (a - y)<sup>2</sup>'''. Таким образом необходимо минимизировать функционал '''Q(w)''': <br /> |
| + | <tex>Q(w) \, = \, \sum_{i=1}^m (a(x_i, w) - y_i)^2 \to \min_w</tex> <br /> | ||
| + | Применим [[метод градиентного спуска]], тогда следующее значение будет иметь вид: | ||
| + | <tex>w \, {:=} \, w \, - \, \eta \nabla Q(w) = w - \eta \( (w,x) - y)*x </tex> ,где <tex>\eta</tex> - темп обучения. | ||
| + | |||
| + | |||
| + | ==Схема обучение ADALINE== | ||
| + | '''Вход:''' | ||
| + | *<tex>X^l</tex> - обучающая выборка <br /> | ||
| + | *<tex>\eta</tex> - темп обучения <br /> | ||
| + | *<tex>\lambda</tex> - параметр сглаживания функционала <tex>Q</tex> <br /> | ||
| + | '''Выход:''' | ||
| + | *Вектор весов <tex>w</tex> <br /> | ||
| + | '''Тело:''' | ||
| + | #Инициализировать веса <tex>w_j \; j = 0, \dots, n</tex>; | ||
| + | #Инициализировать начальную оценку функционала: | ||
| + | #:: <tex>Q \, {:=} \, \sum_{i=1}^l (a(x_i, w) - y_i)^2</tex>; | ||
| + | #Повторять: | ||
| + | ##Выбрать объект <tex>x_i</tex> из <tex>X^l</tex> (например, случайным образом); | ||
| + | ##Вычислить ошибку: | ||
| + | ##::<tex>\varepsilon_i \, {:=} \, ((x_i, w)- y_i)^2</tex>; | ||
| + | ##Сделать шаг градиентного спуска: | ||
| + | ##::<tex>w \, {:=} w - \eta \( (x_i, w) - y_i)*x_i</tex>; | ||
| + | ## Оценить значение функционала: | ||
| + | ##::<tex>Q \, {:=} \, (1 \, - \, \lambda)Q \, + \, \lambda\varepsilon_i</tex>; | ||
| + | #Пока значение <tex>Q</tex> не стабилизируется и/или веса <tex>w</tex> не перестанут изменяться. | ||
| + | |||
=== Связь обучения ADALINE с Stochastic Gradient === | === Связь обучения ADALINE с Stochastic Gradient === | ||
Версия 19:24, 5 января 2010
| | Данная статья является непроверенным учебным заданием.
До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}. См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |
Адаптивный линейный элемент(Адаптивный линейный нейрон или ADALINE) - частный случай линейного классификатора или искусственной нейронной сети с одним слоем. Был предложен Видроу и Хоффом в 1960 году, развивая математическую модель нейрона МакКаллока–Питтса.
Содержание |
Общая схема работы ADALINE
Схема работы ADALINE несколько напоминает работу биологического нейрона:
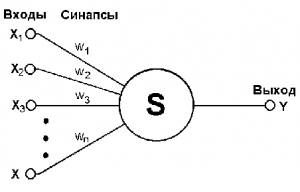
На вход подаётся вектор импульсов xn ,состоящий из n числовых признаков. Внутри нейрона импульсы складываются с некоторыми весами wj, j = 1..n и, если суммарный импульс S(x) = превысит порог активации w0, то нейрон возбуждается и выдаёт некоторое значение a(x) = S(x) - w0.
Если добавить фиктивный импульс-признак x0 ≡ -1 и ему сопоставить вес w0 - порог активации, то формулу выхода Y(x) можно выписать более компактно:
a(x) =(w,x) , где (w,x) - скалярное произведение, w и x - векторы весов и импульсов-признаков соответственно.
Обучение ADALINE
Пусть дана обучающая выборка: множество входных значений X и множество выходящих значений Y, такие что каждому входу xj соответствует yj - выход, j = 1..m. Необходимо по этим данным построить ADALINE, которая допускает наименьшее количество ошибок на этой обучающей выборке.
Обучение ADALINE заключается в подборе "наилучших" значений вектора весов w. Какие значение весов лучше определяет
функционал потерь.В ADALINE используется функционал, предложенный Видроу и Хоффом, L(a,x) = (a - y)2. Таким образом необходимо минимизировать функционал Q(w):
Применим метод градиентного спуска, тогда следующее значение будет иметь вид:
,где
- темп обучения.
Схема обучение ADALINE
Вход:
- обучающая выборка
- темп обучения
- параметр сглаживания функционала
Выход:
- Вектор весов
Тело:
- Инициализировать веса
;
- Инициализировать начальную оценку функционала:
-
;
-
- Повторять:
- Выбрать объект
из
(например, случайным образом);
- Вычислить ошибку:
;
- Сделать шаг градиентного спуска:
;
- Оценить значение функционала:
;
- Выбрать объект
- Пока значение
не стабилизируется и/или веса
не перестанут изменяться.
Связь обучения ADALINE с Stochastic Gradient
Схема обучения ADALINE соответствует схеме обучения линейного классификатора методом стохастического градиента c линейной функцией активации φ(z) = z и квадратичной функцией потерь L(a,x) = (a - y)2.

