Обнаружение жизненного цикла товаров (отчет)

Материал из MachineLearning.

Версия от 12:26, 3 октября 2013; Mikethehuman (Обсуждение | вклад)
(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)
Перейти к: навигация, поиск

Введение в проект

Описание проекта

Цель проекта

Цель проекта - прогнозирование еженедельных покупок товаров. Горизонт прогнозирования - одна неделя.

Обоснование проекта

Полученные результаты могут быть использованы для планирования закупок товаров магазинами.

Описание данных

Дан региональный классификатор магазинов, товарный классификатор, stock keeping unit, список праздничных дней и, отдельно по каждому товару, список дней, в которые проводились промо-акции.

Критерии качества

Прогноз производится отдельно по каждому из товаров. Мы составляем еженедельный прогноз с горизонтом неделя, основанный на предыдущей истории покупок. Критерием качества служит средний модуль отклонения прогноза от реальной величины покупок.

Требования к проекту

Средний модуль отклонения для нашего алгоритма должен быль меньше, чем для скользящего среднего за предыдущий месяц.

Выполнимость проекта

Прогнозирование покупок товаров в праздничные дни и во время промо-акций является отдельной задачей и в данном проекте не рассматривается.

Используемые методы

Предполагается, что жизнь товара на рынке можно разбить на характерные этапы, на каждом из которых величина покупок имеет свой вид функциональной зависимости от предыдущей истории покупок.

Постановка задачи

Заданы временные ряды продаж товаров x_{ij}(t) \in R — продажи i-ого товара в j-ом магазине за неделю t (i \in I, I — множество товаров; j \in J, J — множество магазинов; t \in N — натуральное число), причем значения продаж известны при t_0 \leq t \leq t_1. Задан t_2 - горизонт прогнозирования. Требуется для всех товаров и всех магазинов спрогнозировать продажи за неделю, следующую после t_1+t_2, то есть значение величины

y_{ij} = x_{ij}(t_1+t_2+1).

Для оценки качества прогнозов будем использовать скользящий контроль, помещая в обучающую выборку значения x_{ij}(t) при t \in [t_0, t_{max}], t_{max} < t_1. Как функционал качества будем использовать

Q_{m}(Y, \hat{Y}) = \sum_{i, j}|y_{ij}-\hat{y}_{ij}|.

Описание алгоритмов

Базовые предположения

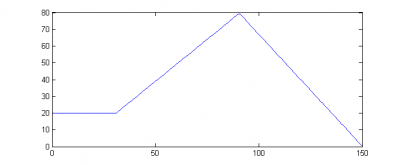
Будем предполагать, что жизненный цикл товара в магазине можно разбить на 3 характерных этапа: вхождение товара на рынок, рост популярности, спад объема продаж. Схематично предполагаемая зависимость может быть изображена в виде (по оси абсцис отложено время прибывания товара на рынке, по оси ординат - еженедельные продажи. Преполагаемая теоретическая зависимость

Математическое описание

Базовый алгоритм

В качестве базового алгоритма выбрано скользящее среднее по каждой паре товар-магазин за 8 предыдущих недель:

\hat{y}_{ij}^0 = \frac{1}{w} s_{ij}(w),

где w=8 — ширина окна,

s_{ij}(w)=\sum_{t = t_1-w-1}^{t_1-1}x_{ij}(t).

Алгоритм учета жизненного цикла

1. Задается два параметра sw и grow.

2. Временной ряд продаж товара разбивается на три отрезка. Первый от момента вхождения \tau_0 до \tau_0+sw. Второй - [\tau_0+sw+1, \tau_0+sw+grow]. Заключительный - от \tau_0+sw+grow+1 до окончания продаж товара.

3. Первый отрезок соответствует этапу вхождения товара на рынок. На нем предполагается использование базового алгоритма для прогнозирования.

4. Втором и третий отрезоки соответствуют росту популярности товара на рынке и спада объема продаж. На них прогноз строится при помощи линейной регрессии: Задается параметр h - число точек для построения прямой.

\hat{y}_{ij}(\tau) = w_0+w_1x_{ij}(t), где (w_0,w_1) = {arg}\min_{(w_0,w_1)}\sum_{t = \tau-h}^{\tau-1}|w_0+w_1x_{ij}(t)-y_{ij}(t)|.

При этом на втором этапе прогнозу запрещается более чем в ε раз меньше скользящего среднего, на третьем прогнозу запрещается быть более чем в σ раз больше скользящего среднего.

Варианты или модификации

Параметрами алгоритма являются sw, h, gr \in N, \ \ \varepsilon, \delta \in (0, \infty), наилучшие значения которых требуется выбрать в результате эксперимента.

Описание системы

  • Описание системы: [1].
  • Файлы системы находятся в папке [2].

Отчет о вычислительных экспериментах

Сравнение алгоритма с базовым

Временные ряды товаров были разбиты на обучение ( k = 100 \ рядов) и контроль ( m = 5915 \ рядов).

В качестве параметров для алгоритма учета жизненного цикла выбран набор, доставляющий локальный минимум функционалу Q_{m} построенному на обучении.

Сравнивались прогнозы базового алгоритма, линейной регрессии ( h =14, \ sw = gr=0 , \ \varepsilon = \delta = \infty ) и алгоритма учета жизненного цикла с параметрами h =14, \ sw = 5, \ gr=30, \ \varepsilon = 1, \ \delta = 2 .

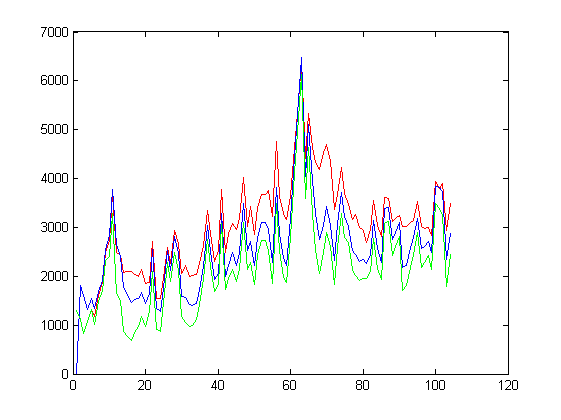
Результаты изображены на графиках, приведенных ниже:

На графике по осям отложены номера недель и величины Q_{m}. Красным цветом изображен график для базового алгоритма, синим - линейной регрессии, зеленым - алгоритма учета жизненного цикла.

На графике по осям отложены номера пар товар-магазин и величины Q_{m}. Красным цветом изображен график для базового алгоритма, синим - линейной регрессии, зеленым - алгоритма учета жизненного цикла.

Таким образом, алгоритм учета жизненного цикла показал лучший результат. Ниже приведены численные результаты работы алгоритмов:

Название алгоритма Значение Q_{m}(Y, \hat{Y}) = \frac{|y_{ij}-\hat{y}_{ij}|}{\sum_{i, j}y_{ij} }
Базовый алгоритм 1.17
Линейная регрессия 1.00
Алгоритм учета жизненного цикла 0.85


Анализ зависимости работы алгоритма от параметров

Зависимость от параметра sw

Проведен анализ работы алгоритма учета жизненного цикла при различных значениях параметра sw (параметры h =14, \ gr=30, \ \varepsilon = 1, \ \delta = 2 \ и фиксированы). Результаты представлены на графике ниже:

На графике по осям отложены значения sw и значения функционала Q_{m}, отнесенные к его значению при sw =5.

Значение данного параметра существенно влияет на качество прогноза. По полученному локально оптимальному значению параметра можно предположить, что решение задачи прогнозирования продаж новых товаров целесообразно выполнить отдельно.

Зависимость от параметра grow

Проведен анализ работы алгоритма учета жизненного цикла при различных значениях параметра grow (параметры h =14, \ sw=5, \ \varepsilon = 1, \ \delta = 2 \ и фиксированы). Результаты представлены на графике ниже:

На графике по осям отложены значения grow и значения функционала Q_{m}, отнесенные к его значению при grow =30.

Зависимость от параметра h

Проведен анализ работы алгоритма учета жизненного цикла при различных значениях параметра h (параметры grow =30, \ sw=5, \ \varepsilon = 1, \ \delta = 2 \ и фиксированы). Результаты представлены на графике ниже:

На графике по осям отложены значения h и значения функционала Q_{m}, отнесенные к его значению при h =14.

Зависимость от параметров \varepsilon \ и \delta

Проведен анализ работы алгоритма учета жизненного цикла при различных значениях параметра \varepsilon (параметры grow =30, \ sw=5, \ h = 14, \ \delta = 2 \ и фиксированы) и при различных значениях параметра \delta (параметры grow =30, \ sw=5, \ h = 14, \ \varepsilon = 1 \ и фиксированы).

Алгоритм с параметрами \varepsilon \in [0, 1] \ и \delta \in [2,\infty] показывает результаты, отличающиеся на менее чем на 0,1% . В то время как значения \varepsilon \in [1, \infty] \ и </tex> и \delta \in [0,1] значительно ухудшают качество работы алгоритма. При \varepsilon = \infty \ и \delta =0 алггоритм совпадает с базовым.

Смотри также

Список литературы

  • Н.Д. Эриашвили, К. Ховард, Ю.А. Цыпкин - Маркетинг: Учебник для вузов.
  • Bishop C. - Pattern Recognition and Machine Learning (Springer, 2006)
  • Воронцов К.В. - Лекции по линейным алгоритмам классификации


Данная статья была создана в рамках учебного задания.
Студент: Участник:Юрий Янович
Преподаватель: Участник:В.В. Стрижов
Срок: 15 декабря 2009


В настоящее время задание завершено и проверено. Данная страница может свободно правиться другими участниками проекта MachineLearning.ru.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://poligon.machinelearning.ru/wiki/index.php?title=%D0%9E%D0%B1%D0%BD%D0%B0%D1%80%D1%83%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5_%D0%B6%D0%B8%D0%B7%D0%BD%D0%B5%D0%BD%D0%BD%D0%BE%D0%B3%D0%BE_%D1%86%D0%B8%D0%BA%D0%BB%D0%B0_%D1%82%D0%BE%D0%B2%D0%B0%D1%80%D0%BE%D0%B2_%28%D0%BE%D1%82%D1%87%D0%B5%D1%82%29»
Личные инструменты