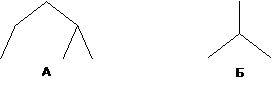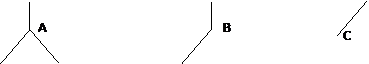Порождение нелинейных регрессионных моделей (пример)

Материал из MachineLearning.

Версия от 12:11, 3 октября 2013; Mikethehuman (Обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Порождение нелинейных регрессионных моделей — порождение функций, зависящих от параметров и от одной или нескольких свободных переменных. Зависимость от параметров предполагается нелинейной.

Содержание

1 Постановка задачи
2 Дополнительные предположения
3 Интерпретация на языке деревьев
4 Альтернативная интерпретация
5 Порождение множества деревьев суперпозиций
6 Обход дерева суперпозиции
7 Уточнение типа функции
8 Подстановка номера функции
9 Выбор оптимальной модели
10 Вычислительный эксперимент
11 Исходный код
12 См. также
13 Литература

Постановка задачи

Задана выборка из $m$ пар $(\mathbf{x}_i,y_i)$ . Задан набор порождающих функций одного и двух аргументов $[G_i]_{i=1}^{n} = [[g_l^{_{(1)}}(w_l,x)]_{l=1}^k,[g_m^{_{(2)}}(w_m,x,y)_{m=k+1}^n]]$ , которые зависят от параметров $\mathbf{w_i}=(w_1,...,w_{W_i})$ и свободных переменных $x,y$ . Функции гладкие параметрические. Требуется создать алгоритм, порождающий лексикографически упорядоченные суперпозиции возрастающей сложности. Каждая суперпозиция является регрессионной моделью одной независимой переменной. Сравнить качество моделей и регрессионные остатки на порожденном множестве.

Дополнительные предположения

Предполагается, что функции $g^{_{(2)}}_i(w_i,x, y)$ корректно работают в случае вызова в виде $g^{_{(2)}}_i(w_i,x)$ .

Интерпретация на языке деревьев

Заметим вначале, что суперпозиция функций $G_i$ может быть задана двоичным деревом $T(V,X)$ , вершины которого $V_i$ ∈ $G_i$ , корень – самая внешняя функция суперпозиции. Под глубиной вершины будем понимать расстояние от неё до корня. Если у вершины один потомок, то соответствующая функция запишется как $g_i(g_j)$ , если два – то $g_i(g_j,g_k)$ , если ноль – то $g_i(x)$ или $g_i(x,x)$ .

Так, дереву А соответствует суперпозиция $2(1(1),2(1,1))$ , а дереву Б – суперпозиция $1(2(1,1))$ .

Альтернативная интерпретация

Эта интерпретация особенно ценна, если нельзя вызвать $g^{_{(2)}}_i(x,x)$ в виде $g^{_{(2)}}_i(x)$ . Изменение состоит в том, что листья дерева суперпозиции считаются не функциями, а свободными переменными. В этом случае дереву А будет соответствовать суперпозиция $2(1(x), 2(x,x))$ дереву Б – суперпозиция $1(2(x,x))$ .

Порождение множества деревьев суперпозиций

Комбинаторная простота этого шага алгоритма заключается в том, что изоморфные деревья задают разные суперпозиции. Однако простые смещения вершин не дают новых деревьев.

Так, деревья А и В различны с точки зрения задаваемых суперпозиций, но деревья А и Б идентичны. Поэтому при машинной реализации можно вообще исключить деревья типа Б, т.е. если из вершины исходит одно ребро, будем «рисовать» его «сверху вниз, справа налево», как в деревьях А и В.
Порождение деревьев осуществим по уровням глубины. Т.е. для задачи порождения деревьев высоты не больше $n$ породим все деревья высоты не больше $n-1$ и запишем их в список $1$ . В список $2$ поместим все деревья высоты ровно $n-1$ . Далее возьмём дерево из списка $2$ , построим всевозможные деревья высоты $n$ из него, получаемые добавлением рёбер к вершинам нижнего уровня глубины, и поместим их в конец списка $1$ . То же проделаем со всеми остальными деревьями списка $2$ .

Обход дерева суперпозиции

Следующий этап алгоритма – это получение по дереву задаваемой им суперпозиции в виде строки символов { $,$ $($ $)$ $1$ $2$ }, где $1$ и $2$ означают $g^{_{(1)}}_i$ и $g^{_{(2)}}_i$ .

Для этого совершим обход дерева в глубину и поставим вершине типа А в соответствие конструкцию $2( , )$ , вершине В – $1( )$ , вершине C – $1$ .

Уточнение типа функции

Для порождения полного списка возможных суперпозиций, в которых вместо $g_i^{_{(1)}}$ и $g_i^{_{(2)}}$ стоят $1$ и $2$ , – нужно, воспользовавшись тем, что $g_i^{_{(2)}}(x,y)$ может быть вызвана как $g_i^{_{(2)}}(x)$ , заменить в каждой строке суперпозиции всеми возможными способами цифру $1$ на $2$ . Это несложно реализуется полным перебором – в каждом вхождении $1$ нужно выбрать, заменять её или нет.

Этот этап будет излишним в реализации альтернативного варианта алгоритма.

Подстановка номера функции

Заключительный этап заключается в том, чтобы по двум спискам с номерами функций: в первом – номера $g_i^{_{(1)}}(x)$ , во втором – $g_i^{_{(2)}}(x,y)$ – и подготовленному на предыдущем шаге списку получить необходимый список суперпозиций. Осуществляется, опять же, полным перебором: рассматриваются все варианты замены $1$ в каждом вхождении на номера из первого списка умножить на все варианты замены $2$ в каждом вхождении на номера из второго списка.

Список, полученный после этого шага, будет искомым.

Выбор оптимальной модели

Необходимо понять, на каком этапе прекращать работу алгоритма и как из полученного множества моделей выбрать нужную. Вопрос выбора встаёт по той причине, что данные всегда зашумлены и функция, идеально приближающая обучающую выборку, может оказаться слишком сложной и, как следствие, неподходящей. Основная идея в том, чтобы ввести два параметра $R$ и $C$ , характеризующие функцию. Параметр $R$ характеризует степень приближения функцией данных на обучающей выборке (например, сумма квадратов остатков). Параметр $C$ характеризует сложность функции. Выбор его может быть самым разнообразным и зависеть от самих функций (например, скорее всего, вес $sin(x)$ или $exp(x)$ много больше веса $ax+b$ ), или же от дерева суперпозиции, или от того и другого. При выборе зависимости $C$ от дерева суперпозиции также есть варианты среди всевозможных характеристик дерева: высоты $h$ , числа вершин $|V|$ , длины наибольшего пути и др. Одна из характеристик (предложена Е.Владиславлевой) – сумма количеств вершин $\sum\|V^i |$ по всем поддеревьям $T^i(V^i, X^i)$ дерева суперпозиции $T(V, X)$ . Под поддеревом понимается дерево, состоящее из некоторой вершины и всех её потомков.

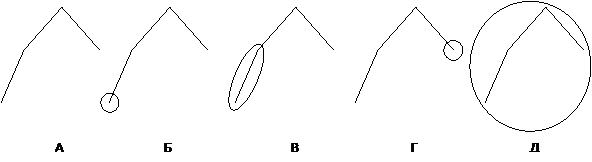
Например, на рисунках Б – Д обведены всевозможные поддеревья дерева А. Сложность по Владиславлевой дерева А равна $1+2+1+4 = 8$ .

Вычислительный эксперимент

Был проведен эксперимент, значения y на сетке по x от 1 до 5 с шагом 0.5 задавались функцией y = sin(sin(x) + sqrt(|x|)) + exp(-x). Суперпозиции искались в алфавите sin(x), cos(x), x+y, sqrt(x). В связи с этим, слагаемое exp(-x) - шумовой фактор. Искались суперпозиции глубины не более 4, с числом вершин не более 5 и вычислением сложности по методу Владиславлевой. Ниже приведен график в координатах C-R, плюсами отмечены модели с лучшим приближением в своем классе сложности. Число рядом - номер в полном списке порожденных моделей (всего их было 2212).

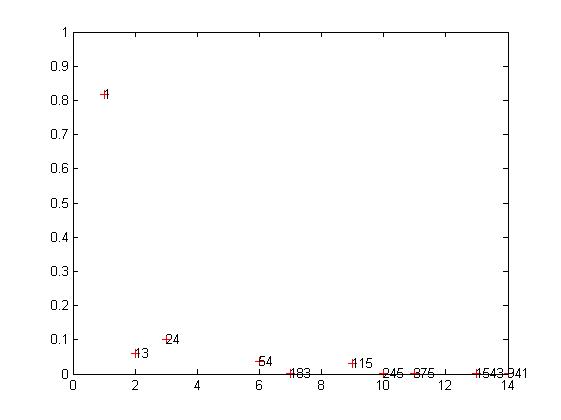
Далее следуют графики моделей. Красной линией изображен график начальной функции.

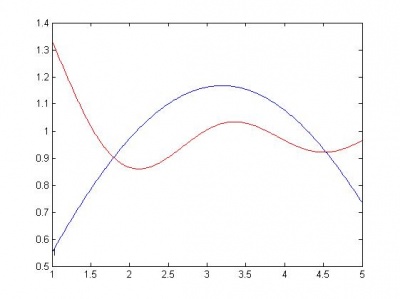
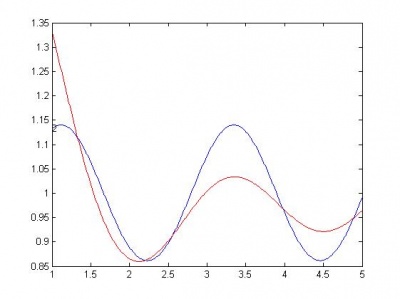
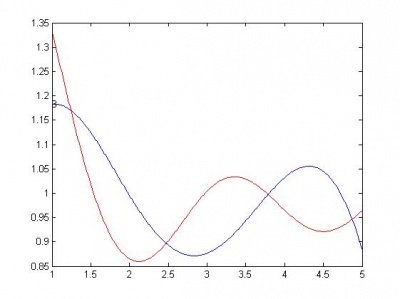
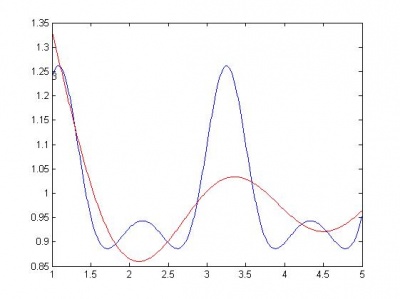
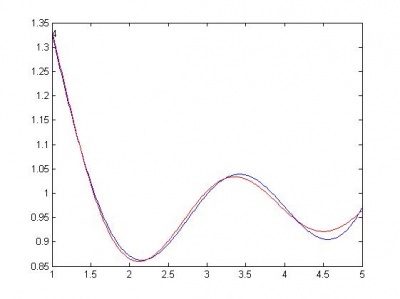
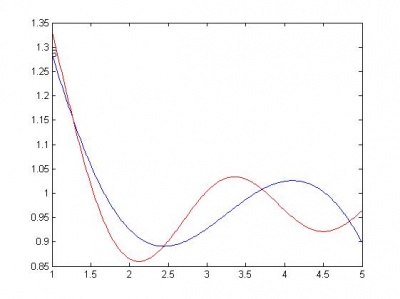
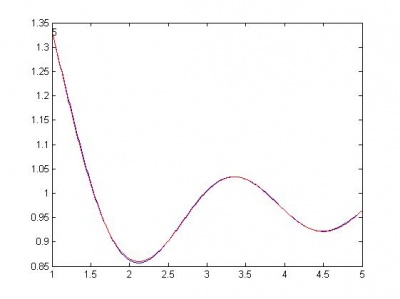
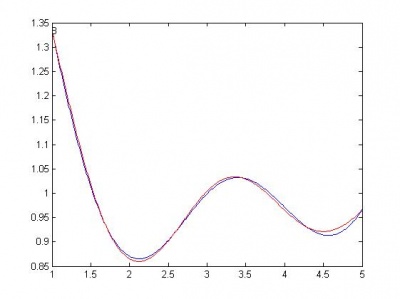
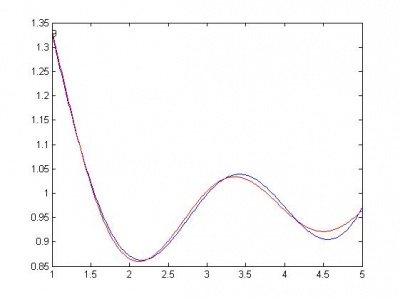
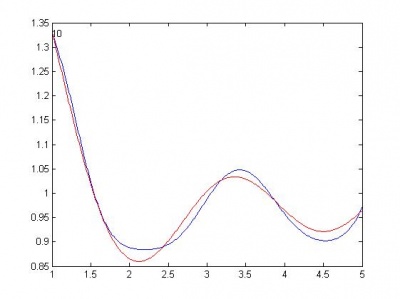
Ниже, по возрастанию сложности, приведены модели. R - сумма квадратов регрессионных остатков. Функции здесь следует понимать следующим образом: sin(x) - w1*sin(w2*x); cos(x) - w1*cos(w2*x); sqrt(x) - w*sqrt(|x|); a+b - w1*a + w2*b. Здесь w, w1, w2 - параметры функции, оптимизируются matlab-функцией nlinfit.

sin(x) , R = 0.8185
cos(cos(x)) , R = 0.0612
sin(x)+cos(x) , R = 0.1001
cos(sin(cos(x))) , R = 0.0357
cos(x)+cos(sin(x)) , R = 5.6*10^-4
cos(sin(x)+sqrt(x)) , R = 0.0294
sin(x)+(cos(x)+cos(x)) , R = 2.3*10^-5
sin(sqrt(x))+cos(sin(x)), R = 1.8*10^-4
(cos(x)+sin(x))+cos(x) , R = 5.6*10^-4
cos(sin(sin(x)+sin(x))) , R = 0.0016

Исходный код

Скачать программную реализацию можно здесь: [1]

См. также

Литература

Стрижов В.В. Поиск параметрической регрессионной модели в индуктивно заданном множестве. [2]
E. Vladislavleva, G. Smits, and D. den Hertog. “Order of Nonlinearity as a complexity measure for models generated by symbolic regression via Pareto genetic programming”, doi 10.1109/TEVC.2008.926486

Данная статья была создана в рамках учебного задания.

Студент: Александр Мафусалов

Преподаватель: В.В.Стрижов

Срок: 28 мая 2010

В настоящее время задание завершено и проверено. Данная страница может свободно правиться другими участниками проекта MachineLearning.ru.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://poligon.machinelearning.ru/wiki/index.php?title=%D0%9F%D0%BE%D1%80%D0%BE%D0%B6%D0%B4%D0%B5%D0%BD%D0%B8%D0%B5_%D0%BD%D0%B5%D0%BB%D0%B8%D0%BD%D0%B5%D0%B9%D0%BD%D1%8B%D1%85_%D1%80%D0%B5%D0%B3%D1%80%D0%B5%D1%81%D1%81%D0%B8%D0%BE%D0%BD%D0%BD%D1%8B%D1%85_%D0%BC%D0%BE%D0%B4%D0%B5%D0%BB%D0%B5%D0%B9_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»

Категории: Нелинейная регрессия | Регрессионный анализ | Практика и вычислительные эксперименты