Участник:Riabenko/Песочница
Материал из MachineLearning.
Задание 2. Исследование свойств многомерного статистического метода на модельных данных
Пример
Исследуем чувствительность однофакторного дисперсионного анализа к расстояниям между выборками и дисперсиям выборок.
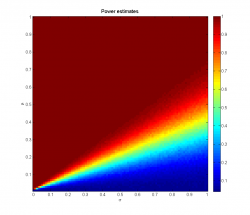
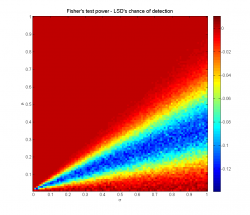
Посмотрим, как от расстояний между выборками и дисперсий зависят средний достигаемый уровень значимости и мощность используемого по умолчанию критерия Фишера:
Для каждой пары значений параметров мощность оценивается как доля выборок, на которых нулевая гипотеза о равенстве всех средних была отвергнута.
Зависимость выглядит естественно: мощность растёт при увеличении расстояний между выборками и уменьшении их дисперсий. Для данного размера выборок средний достигаемый уровень значимости не превосходит 0.05 для всех значений , мощность при этом не опускается ниже 0.7.
Для сгенерированных выборок проведём сравнение средних при помощи метода LSD. Для каждой пары средних метод даёт точечную оценку разности между ними и 95% доверительный интервал для этой разности. Так как
, для оценки параметра
можно использовать среднее между оценками
и
.
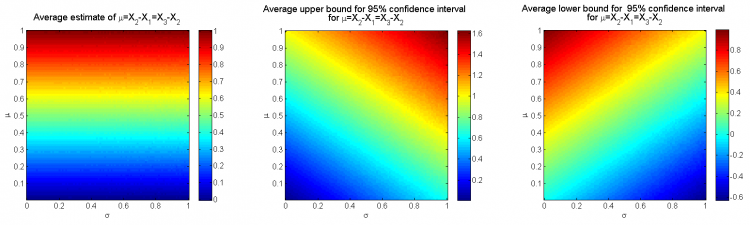
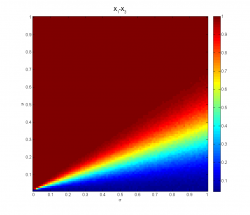
Рассмотрим усреднённые оценки и границы доверительных интервалов:
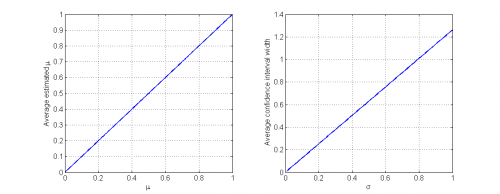
Заметим, что усреднённая точечная оценка расстояния между выборками является точной и не зависит от дисперсии выборок, а ширина доверительного интервала для
, напротив, зависит только от
:
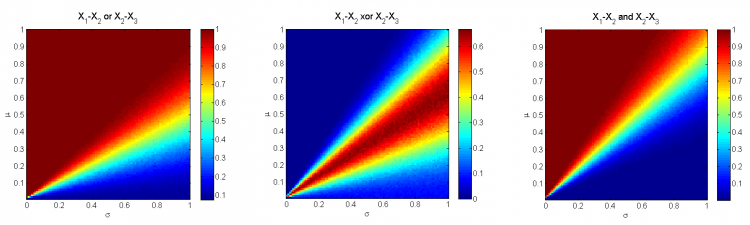
Можно считать, что метод детектирует значимую на уровне разность между средними значениями выборок, если соответствующий 95% доверительный интервал для неё не содержит нуля. Рассмотрим для каждой пары значений параметров
доли выборок, на которых разница в
между средними пар выборок
и
была детектирована.
Заметим, что при достаточно велик шанс детектировать различия между средними только одной из двух абсолютно равнозначных пар выборок – в конусе
вероятность такого события составляет 0.4-0.6.
Оценим долю выборок, на которых была детектирована разница между средними выборок :
Сравнивая полученные оценки с построенными выше оценками мощности критерия Фишера, можно заметить, что метод ЛСД обладает большей чувствительностью к разнице между средними значениями выборок. Различия заметны в области , где мощность критерия Фишера может быть ниже более, чем на 0.12.
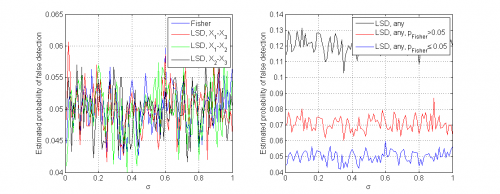
Наконец, исследуем поведение методов при
Доля выборок, на которых критерий Фишера обнаружил несуществующие различия между средними, не зависит от и колеблется около уровня значимости 0.05, что свидетельствует о корректности метода. Рассматриваемые независимо, доли выборок, на которых метод LSD нашёл различия между средними каких-либо пар выборок
,
,
, также не зависят от
и примерно равны 0.05. Однако совместная вероятность неверного обнаружения хотя бы одного различия между парами выборок достаточно высока – около 0.12, что вызвано эффектом множественной проверки гипотез (независимо проверяются гипотезы о равенстве средних трёх пар выборок). При этом для выборок, на которых критерий Фишера показал достигаемый уровень значимости ниже 0.05, средняя доля ложно обнаруженных методом LSD различий между выборками также равна примерно 0.05.
Таким образом, данные этого модельного эксперимента показывают, что, несмотря на то, что мощность метода LSD выше, чем критерия Фишера, использовать метод LSD необходимо только в том случае, если критерий Фишера показал наличие каких-либо различий между средними выборок, поскольку в случае независимого использования LSD вероятность случайно обнаружить несуществующие различия превышает номинальный уровень значимости (и будет тем выше, чем больше рассматривается выборок).