Математические основы теории прогнозирования (курс лекций)/2012/Задание СФ

Материал из MachineLearning.

Перейти к: навигация, поиск
Внимание! Текст задания находится в стадии формирования. Убедительная просьба не приступать к выполнению данного задания до тех пор, пока это предупреждение не будет удалено.


Содержание

Основная статья: Математические основы теории прогнозирования (курс лекций)

Срок сдачи задания: 30 августа 2012, 23:59

Данное практическое задание предназначено, в первую очередь, для студентов Севастопольского филиала, которые имеют задолженность по курсу МОТП и не имеют возможности присутствовать в Москве на пересдачах осенью. Тем не менее, это задание могут выполнять и московские студенты ВМиК, которые имеют задолженность по курсу МОТП. Оценка за это задание будет итоговой оценкой по курсу МОТП.

Цель данного задания состоит в том, чтобы студенты познакомились на практике с популярными методами решения задач классификации и кластеризации — методом опорных векторов и методом к-средних, а также с базовыми аспектами, с которыми приходится сталкиваться при решении задач машинного обучения — проблемой переобучения и проблемой подбора структурных параметров алгоритма (таких как коэффициент С, параметры ядровых функций, количество кластеров в данных).

Необходимая теория

Метод опорных векторов

Иллюстрация линейного разделения выборки с помощью метода опорных векторов, зелеными кружками отмечены опорные объекты
Иллюстрация линейного разделения выборки с помощью метода опорных векторов, зелеными кружками отмечены опорные объекты

Рассматривается задача классификации на два класса. Имеется обучающая выборка \{\vec{x}_n,t_n\}_{n=1}^N, где \vec{x}_n\in\mathbb{R}^d — вектор признаков для объекта n, а t_n\in\{-1,+1\} — его метка класса. Задача заключается в предсказании метки класса t_{new} для объекта, представленного своим вектором признаков \vec{x}_{new}.

В методе опорных векторов предсказание метки класса осуществляется по знаку линейной функции:

t(\vec{x}_{new}) = \begin{cases}+1,\ f(\vec{x}_{new})=\vec{w}^T\vec{x}_{new} + b = \sum_{j=1}^dw_jx_{j,new} + b\ge 0,\\-1,\ f(\vec{x}_{new})<0.\end{cases}

Для поиска весов \vec{w} и величины сдвига b решается следующая задача квадратичного программирования:

\sum_{n=1}^N\lambda_n - \frac{1}{2}\sum_{n,m=1}^N\lambda_n\lambda_mt_nt_m\vec{x}_n^T\vec{x}_m\rightarrow\max_{\vec{\lambda}}

\sum_n\lambda_nt_n=0,

0\le\lambda_n\le C.

Здесь C>0 — параметр алгоритма, который задает компромисс между точностью распознавания обучающей выборки и величиной зазора между данными и гиперплоскостью (надежностью классификации).

После решения задачи квадратичного программирования оптимальный вектор весов вычисляется как

\vec{w} = \sum_{n=1}^N\lambda_nt_n\vec{x}_n.

Очевидно, что только те объекты обучающей выборки, для которых \lambda_n\neq 0, влияют на оптимальный вектор весов. Такие объекты получили название опорных. Пусть \exist n_*:\ 0<\lambda_{n_*}<C. Тогда оптимальная величина сдвига гиперплоскости b определяется как

b = t_{n_*} - \vec{w}^T\vec{x}_{n_*}.

На практике здесь лучше проводить усреднение по всем n:\ 0<\lambda_n<C. Если в оптимальном \vec{\lambda} все коэффициенты равны только нулю и C, то тогда коэффициент b может быть найден перебором путем минимизации ошибки распознавания обучающей выборки.

Использование ядровых функций

Иллюстрация нелинейного разделения выборки с помощью метода опорных векторов с радиальной ядровой функцией, зелеными кружками отмечены опорные объекты
Иллюстрация нелинейного разделения выборки с помощью метода опорных векторов с радиальной ядровой функцией, зелеными кружками отмечены опорные объекты

Для построения нелинейных решающих правил с помощью метода опорных векторов вводится понятие ядровой функции. Пусть имеется преобразование из исходного признакового пространства \mathbb{R}^d в новое пространство H, задаваемое функцией \phi:\mathbb{R}^d\rightarrow H. Пусть также имеется ядровая функция K, которая задает скалярное произведение в новом пространстве H:

K(\vec{x},\vec{y}) = \phi(\vec{x})^T\phi(\vec{y}),\ \forall\vec{x},\vec{y}.

Тогда для построения линейной разделяющей гиперплоскости в новом пространстве H достаточно знать лишь ядровую функцию K и не требуется знать само преобразование \phi. В этом случае на этапе обучения метода решается следующая задача квадратичного программирования:

\sum_{n=1}^N\lambda_n - \frac{1}{2}\sum_{n,m=1}^N\lambda_n\lambda_mt_nt_mK(\vec{x}_n,\vec{x}_m)\rightarrow\max_{\vec{\lambda}},

\sum_n\lambda_nt_n = 0,

0\le \lambda_n\le C.

При этом скалярное произведение оптимального вектора весов \vec{w} и произвольного объекта \vec{x} определяется как

\vec{w}^T\vec{x} = \sum_{n=1}^N\lambda_nt_nK(\vec{x}_n,\vec{x}).

По-прежнему, только опорные объекты (для которых \lambda_n\neq 0) вносят вклад в значение данного скалярного произведения. Величина сдвига гиперплоскости, как и раньше, определяется как

b = \frac{\sum_{n:0<\lambda_n<C}(t_n - \vec{w}^T\vec{x}_n)}{\sum_{n:0<\lambda_n<C}1}.

Если все коэффициенты \lambda_n принимают только крайние значения, то оптимальный сдвиг b находится путем минимизации числа ошибок на обучающей выборке.

Ядровая функция, как правило, выбирается в одном из следующих параметрических семейств:

  1. Линейная: K(\vec{x},\vec{y}) = \vec{x}^T\vec{y},
  2. Степенная: K(\vec{x},\vec{y}) = (\vec{x}^T\vec{y}+1)^r,\ r\in\mathbb{N}.
  3. Радиальная: K(\vec{x},\vec{y}) = \exp\left(-\frac{|\vec{x}-\vec{y}\|^2}{2\gamma^2}\right),\ \gamma>0.

В случае степенной ядровой функции делается неявное предположение о том, что данные отнормированы на нулевой центр и единичную дисперсию. В этом случае, по неравенству Коши-Буняковского, величина \vec{x}^T\vec{y}+1 всегда будет неотрицательной.

Скользящий контроль

В методе опорных векторов параметр регуляризации C, а также параметры ядровых функций (например, параметр \gamma в радиальной ядровой функции) являются структурными параметрами, которые не могут быть настроены путем минимизации числа ошибок на обучающей выборке. Для их настройки используются критерии выбора модели, например, скользящий контроль.

Обозначим обучающую выборку через Y=(X,\vec{t}), а через a(\vec{x},Y) — результат прогноза метки класса для объекта \vec{x}, полученный с помощью алгоритма a, обученного по выборке Y. При K-кратном скользящем контроле обучающая выборка Y разбивается на K равных частей Y=Y_1\sqcup Y_2\sqcup\dots\sqcup Y_K. Общая величина ошибки на K-кратном скользящем контроле вычисляется как

Error_{cv} = \frac{1}{N}\sum_{k=1}^K\ \sum_{n:\vec{x}_n\in Y_k}I[t_n \neq a(\vec{x}_n, Y_{\backslash k})].

Здесь через Y_{\backslash k} обозначена обучающая выборка без части Y_k, а через I[t \neq y] — индикаторная функция, равная единице при выполнении условия t \neq y.

Наиболее популярная версия скользящего контроля — усреднение Error_{cv} по пяти независимым запускам 2-кратного скользящего контроля. При таком подходе необходимо обучать алгоритм только по половине обучающей выборки (что происходит быстрее, чем обучение, например, по 9/10 от объема обучающей выборки). Во-вторых, здесь требуется всего 10 различных обучений (что гораздо меньше, чем, например, объем обучающей выборки N при разбиении выборки на K=N частей).

Настройка параметра регуляризации C с помощью скользящего контроля производится следующим образом. Выбирается набор возможных значений C, например, 2^{-5},2^{-4.9},\dots,2^{4.9},2^{5}. Для каждого из этих значений вычисляется величина ошибки скользящего контроля (например, с помощью усреднения по пяти запускам 2-кратного скользящего контроля). В результате выбирается такое значение C, для которого величина ошибки скользящего контроля является наименьшей. В том случае, если требуется настроить два параметра, например C и \gamma в радиальных базисных функциях, то выбирается двухмерная сетка значений параметров и находится та пара, для которой ошибка на скользящем контроле является наименьшей.

Схема решения задач классификации/регрессии

В простейшем случае для решения задачи классификации/регрессии имеющаяся в распоряжении выборка разбивается на три подвыборки: обучающую, валидационную и тестовую. Сначала выбирается некоторая модель алгоритмов, например, линейная регрессия с полиномиальными базисными функциями. По обучающей выборке в скользящем контроле настраиваются все структурные параметры выбранной модели (для линейной регрессии с полиномиальными базисными функциями в качестве таковых выступают коэффициент регуляризации и степень полинома). Затем с выбранными значениями структурных параметров производится обучение модели алгоритмов по обучающей выборке. Полученный алгоритм тестируется на обучающей и валидационной выборке. В том случае, если значения обеих ошибок значимо отличаются друг от друга (следовательно, есть переобучение) или их значения близки между собой и достаточно большие (значит, есть недообучение), то выбранная модель алгоритмов признается неудачной и выбирается другая модель алгоритмов (более простая, если ранее было обнаружено переобучение, или более сложная, если ранее было обнаружено недообучение). После того, как удается найти хорошую модель алгоритмов (у которой нет переобучения и недообучения), обучающая и валидационная выборка объединяются между собой и используются в качестве обучающей для настройки структурных параметров по скользящему контролю и последующего обучения в найденной хорошей модели алгоритмов. Затем полученный алгоритм тестируется на объединенной обучающей и тестовой выборке. Если обе ошибки близки между собой и достаточно маленькие по значению, то такой алгоритм признается оптимальным для решения задачи классификации/регрессии.

Зачастую имеющаяся в распоряжении выборка прецедентов является небольшой по объему и поэтому не может быть разбита на три достаточно репрезентативные подвыборки. В этом случае выборка разбивается только на обучающую и валидационную, и найденная по описанной выше схеме наилучшая модель алгоритмов не тестируется на отдельной тестовой выборке. Такой подход является менее корректным по сравнению с предыдущим, т.к. мерой качества алгоритма здесь выступает величина, которая подвергалась оптимизации на имеющихся данных. Поэтому здесь возможен эффект переобучения на уровне моделей алгоритмов. Тем не менее, во многих практических ситуациях данная схема дает вполне приемлемый результат.

Формулировка задания

Для выполнения задания на оценку «удовлетворительно» необходимо выполнить следующие пункты:

  1. Реализовать процедуру обучения/тестирования/подбора структурных параметров метода опорных векторов по описанному ниже прототипу;
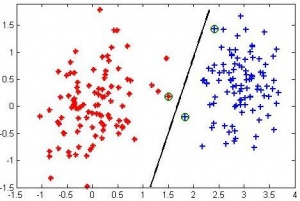
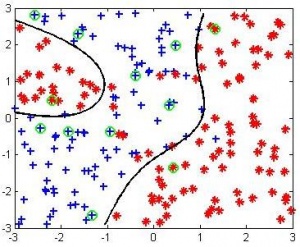
  2. Продемонстрировать на модельных данных для метода опорных векторов эффект переобучения (маленькая ошибка на обучении, большая ошибка на тесте), эффект недообучения (ошибки на обучении и тесте близки между собой и большие по величине) и ситуацию нормальной работы (ошибки на обучении и тесте близки между собой и маленькие по величине);
  3. Решить с помощью метода опорных векторов практическую задачу распознавания рукописных цифр (описание задачи см. ниже) для нескольких произвольных пар цифр;
  4. Составить отчет в формате PDF обо всех проведенных исследованиях; данный отчет должен содержать необходимые графики и описание экспериментов, выводы необходимых формул, описание полученных результатов решения практических задач, общие выводы по исследованию.

Для выполнения задания на оценку «хорошо» необходимо дополнительно к вышеуказанным пунктам выполнить:

  1. Реализовать процедуру кластеризации по методу к-средних по описанному ниже прототипу;
  2. Продемонстрировать на модельных данных для метода к-средних результаты адекватной и неадекватной кластеризации при условии, что истинное количество кластеров известно;
  3. Применить метод кластеризации к-средних для уменьшения объема обучающей выборки в практической задаче распознавания рукописных цифр для повышения скорости обучения метода опорных векторов;
  4. Результаты всех проведенных исследований добавить в отчет.

Для выполнения задания на оценку «отлично» необходимо дополнительно к вышеуказанным пунктам выполнить:

  1. Предложить и реализовать процедуру обучения/тестирования/подбора структурных параметров метода опорных векторов для случая многих классов;
  2. Применить многоклассовый метод опорных векторов для практической задачи распознавания рукописных цифр;
  3. Результаты всех проведенных исследований добавить в отчет.

Спецификация реализуемых функций

Задание выполняется в среде MATLAB. Необходимые алгоритмы должны быть реализованы по прототипам, указанным ниже.

Обучение метода опорных векторов
a = svm_train(X, t, options)
ВХОД
X — обучающая выборка, матрица типа double размера N x D, где N — число объектов, D — число признаков.
t — метки классов для объектов обучения, вектор типа double размера 1 x N, возможны произвольные числовые метки;
options — (необязательный аргумент) набор дополнительных параметров, структура размера 1 x 1, возможны следующие названия полей и их значения:
  'С' — значение коэффициента регуляризации (по умолчанию = 1);
  'С_tuning' — флаг использования скользящего контроля для настройки коэффициента регуляризации, тип logical, если false, то используется значение для С (по умолчанию = false);
  'kernel' — семейство используемых ядровых функций, тип char размера 1 x S, возможные значения 'linear', 'polynomial', 'rbf' (по умолчанию = 'linear');
  'kernel_param' — значение параметра для ядровой функции, тип double размера 1 x 1, для семейства 'rbf' здесь задается значение параметра gamma, для семейства 'polynomial' — значение степени (по умолчанию = 1);
  'kernel_tuning' — флаг использования скользящего контроля для подбора параметров ядровых функций, тип logical, если false, то используется значение из kernel_param (по умолчанию = false);
  'display' — параметр отображения, тип logical, если false, то на экране ничего не отображается, если true, то отображается текущий статус вычислений в произвольной форме (какие значения параметров пробуются, какие ошибки на скользящем контроле получаются, какие итоговые значения параметров оказались наилучшими и т.д.);
ВЫХОД
a — обученный метод опорных векторов, структура размера 1 x 1, поля структуры имеют следующие имена и значения:
'lambdat' - вектор из произведений коэффициентов lambda на метки классов t, вектор типа double размер 1 x M, где M — количество опорных векторов;
'b' — коэффициент сдвига, число;
'support_objects' — опорных объекты, матрица типа double размера M x D;
'kernel' — семейство используемых ядровых функций, совпадает с входным значением 'kernel';
'kernel_param' — параметр ядровой функции, совпадает с входным значением 'kernel_param';

Обратите внимание: параметры N и D определяются неявно по размеру соответствующих элементов.

Тестирование метода опорных векторов
[Outputs, Answers, ErrorRate] = svm_test(a, X, t)
ВХОД
a — обученный метод опорных векторов, структура, которую возвращает функция svm_train;
X — тестовая выборка, матрица типа double размера N_test x D;
t — (необязательный аргумент), истинные значения меток класса для тестовой выборки, вектор типа double размера 1 x N_test.
ВЫХОД
Outputs — значения линейной функции f(\vec{x}) для объектов тестовой выборки, вектор типа double размера 1 x N_test;
Answers — спрогнозированные метки класса для объектов тестовой выборки, вектор типа double размера 1 x N_test;
ErrorRate — процент допущенных ошибок классификации, если вектор t задан, и -1 в обратном случае.

Рекомендации по выполнению задания

1. Эффективное программирование под MATLAB предполагает активнейшее использование векторных и матричных операций. В частности, по возможности следует избегать любых циклов. Например, для вычисления матрицы попарных расстояний между набором объектов, задаваемых матрицами X и Y, можно воспользоваться свойством ||\vec{x}-\vec{y}||^2=||\vec{x}||^2 - 2\vec{x}^T\vec{y} + ||\vec{y}||^2, что в MATLAB может быть реализовано как 

    normX = sum(X.^2,2);
    normY = sum(Y.^2,2);
    diffXY = bsxfun(@plus, bsxfun(@plus, -2*X*Y', normX), normY');

2. При работе с выборками для устойчивости всех производимых вычислений рекомендуется осуществлять нормировку выборки независимо для каждого признака таким образом, чтобы среднее значение по выборке равнялось нулю, а выборочная дисперсия — единице. При этом следует иметь в виду, что для тестовых выборок нужно использовать нормировочные коэффициенты, полученные для обучающих выборок.

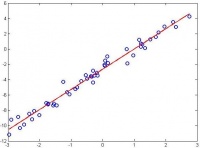
3. Проверять корректность реализации обучения и тестирования линейной/логистической регрессии следует, в первую очередь, на модельных данных. Например, для проверки линейной регрессии можно сгенерировать данные с одним признаком, в которых регрессионная переменная вычисляется как значение полинома некоторой степени от значения признака со сгенерированными коэффициентами плюс небольшой нормальный шум. Тогда при обучении линейной регрессии с полиномиальными базисными функциями и правильной степенью полинома результат предсказания должен быть очень хорошим. Эту ситуацию можно отобразить и визуально. Например, для случая полинома первой степени картинка может выглядеть так:

Кроме того, при автоматическом определении степени полинома по скользящему контролю выбираемое значение степени должно совпадать или быть близким к истинному.

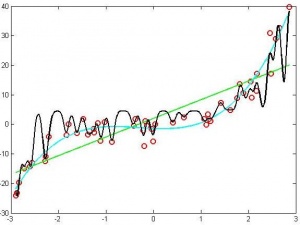
4. Эффекты переобучения/недообучения для линейной/логистической регрессии можно продемонстрировать следующим образом. Для линейной регрессии достаточно сгенерировать одномерные данные с полиномом 3-ей степени. Тогда обучение линейной регрессии с полиномиальными базисными функциями первой степени должно приводить к недообучению, >6-ой степени — к переобучению, а 3-ей степени — к адекватному восстановлению зависимости. Для логистической регрессии можно сгенерировать двухмерные данные с существенно нелинейной разделяющей поверхностью. Тогда обучение логистической регрессии с радиальными базисными функциями и маленьким значением \gamma должно приводить к недообучению, с большим значением \gamma — к переобучению, а некоторое среднее значение \gamma будет соответствовать адекватной разделяющей поверхности.

Различные модели линейной регрессии. Зеленая кривая — недообучение, черная кривая — переобучение, голубая кривая — адекватная зависимость
Различные модели линейной регрессии. Зеленая кривая — недообучение, черная кривая — переобучение, голубая кривая — адекватная зависимость
Различные модели логистической регрессии. Зеленое решающее правило — недообучение, черное решающее правило — переобучение, голубое решающее правило — адекватное разделение данных
Различные модели логистической регрессии. Зеленое решающее правило — недообучение, черное решающее правило — переобучение, голубое решающее правило — адекватное разделение данных

Описание практических задач

Определение предела прочности бетона Классификация вин по месту происхождения
Задача состоит в том, чтобы спрогнозировать уровень давления, при котором конкретная бетонная смесь разрушается, в зависимости от процента содержания в ней цемента, воды, возраста смеси и др. показателей. Исходные данные и подробное описание задачи можно скачать здесь. Имеется набор вин, произведенных в одном регионе Италии, но в трех разных винодельнях. Задача состоит в том, чтобы определить конкретную винодельню (конкретное место происхождения вина) по данным химического анализа вина. Эти данные включают в себя такие параметры как крепость, содержание яблочной кислоты, содержание различных видов флавоноидов и др. Исходные данные и подробное описание задачи можно скачать здесь.

Процедура сдачи задания

Оформление задания

Необходимо в срок до 1 сентября 2011 прислать выполненный вариант задания письмом по адресу bayesml@gmail.com с темой «Задание СФ, ФИО, номер группы». Убедительная просьба присылать выполненное задание только один раз с окончательным вариантом. Новые версии будут рассматриваться только в самом крайнем случае. Также убедительная просьба строго придерживаться заданной выше спецификации реализуемых функций. Очень трудно проверять большое количество заданий, если у каждого будет свой формат реализации.

Письмо должно содержать:

  • PDF-файл с описанием проведенных исследований (отчет должен включать в себя описание выполнения каждого пункта задания с приведением соответствующих графиков, изображений, чисел)
  • Файлы linreg_train.m, linreg_test.m, logreg_train.m, logreg_test.m или аналогичные им исполняемые файлы
  • Набор вспомогательных файлов при необходимости

Защита задания

После сдачи выполненного задания и его проверки необходимо будет защитить свое задание. В том случае, если в какой-то части выполненного задания будет обнаружен плагиат с заданием другого студента, то задание не будет засчитано для обоих студентов! Защита задания будет осуществляться с помощью видео-чата для студентов СФ и во время осенних пересдач для московских студентов. Студенту будет предложен ряд вопросов по присланному коду и проведенным исследованиям. Кроме того, возможны задания по небольшой модификации кода в режиме онлайн.

Источник — «http://poligon.machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5_%D0%BE%D1%81%D0%BD%D0%BE%D0%B2%D1%8B_%D1%82%D0%B5%D0%BE%D1%80%D0%B8%D0%B8_%D0%BF%D1%80%D0%BE%D0%B3%D0%BD%D0%BE%D0%B7%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D1%8F_%28%D0%BA%D1%83%D1%80%D1%81_%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D0%B9%29/2012/%D0%97%D0%B0%D0%B4%D0%B0%D0%BD%D0%B8%D0%B5_%D0%A1%D0%A4»
Личные инструменты