Символьная регрессия и структурное расстояние между моделями (пример)
Материал из MachineLearning.
Символьная регрессия — метод построения регрессионных моделей путем перебора различных произвольных суперпозиций функций из некоторого заданного набора. Суперпозиция функций при этом называется «программой», а стохастический оптимизационный алгоритм построения таких суперпозиций называется генетическим программированием.
Под структурным расстоянием в данном случае понимается количественная оценка степени структурного различия помеченных графов, соответствующих суперпозициям, которая зависит от размера их наибольшего общего подграфа. Чем больше общий подграф, тем больше структурное подобие моделей.
Содержание |
Постановка задачи
Задана выборка — множество значений свободных переменных и множество
соответствующих им значений зависимой переменной. Обозначим оба эти множества как множество исходных данных
.
Также задано множество гладких
параметрических функций
. Первый аргумент функции
— вектор-строка параметров
, последующие — переменные из множества действительных чисел, рассматриваемые как элементы вектора свободных переменных.
Рассмотрим произвольную суперпозицию, состоящую из не более чем
функций
. Эта суперпозиция задает параметрическую регрессионную модель
. Регрессионная модель
зависит от вектора свободных переменных
и от вектора параметров
. Вектор
состоит из присоединенных векторов-параметров
функций
, то есть,
, где
— знак присоединения векторов. Обозначим
— множество всех суперпозиций, индуктивно порожденное элементами множества
.
Требуется выбрать такую модель , которая доставляет максимум заданного функционала
, а также исследовать вектор попарных расстояний между моделями популяции.
Сведения о структурных расстояниях ( метриках ) на множестве помеченных графов
Помеченный граф - это граф, вершинам и ребрам которого приписываются определенные метки. Пусть - конечный, связный, помеченный, неориентированный граф без петель и кратных ребер, имеющий множество вершин
и множество ребер
Рассмотрим графы и
. Пусть
- их наибольший общий подграф (содержит больше ребер, чем любой другой общий подграф). Тогда функции
и
будет метрикой (доказательство этого факта - в статье Макарова Л.И.)
Алгоритм выбора оптимальной модели
Поиск оптимальной модели происходит на множестве порождаемых моделей на каждой итерации алгоритма.
Перед работой алгоритма заданы множество измеряемых данных и множество гладких
функций
.
Задан начальный набор конкурирующих моделей,
, в котором каждая модель
есть суперпозиция функций
.
Если нет начального набора моделей, то он порождается случайным образом.
Далее выполняется последовательность шагов, приведенных ниже.
1. Для каждой модели
отыскиваются параметры
(в данном случае была использована стандартная функция "nlinfit" Matlab) и вычисляется значение минимизируемого функционала для каждой модели.
2. Заданы следующие правила построения производных моделей
. Для каждой модели
строится производная
модель
. В
произвольно выбирается функция
. Выбирается произвольная модель
из
и ее произвольная функция
.
Модель
порождается из модели
путем замещения
функции
с ее аргументами на функцию
с ее
аргументами.
3. С заданной вероятностью каждая модель
подвергается изменениям. В изменяемой модели выбирается
-тая
функция, причем закон распределения вероятности выбора
функции
задан. Из множества
случайным образом
выбирается функция
и замещает функцию
.
Вектор параметров этой
функции
равен нулю или назначается при задании
.
4. При выборе моделей из объединенного множества родительских и
порожденных моделей в соответствии со значением функционала
наилучших, которые используются в дальнейших
итерациях.
Алгоритм остановливается при достижении ошибки, не превосходящей заданную, или через заданное количество раз.
На каждой итерации алгоритма также исследуются попарные структурные расстояния между моделями.
Вычислительный эксперимент
Исследовалась работа алгоритма на модельных и реальных данных.
В качестве базовых были использованы 7 функций ,
,
,
,
,
,
.
Алгоритм имеет следующие параметры :
- MODEL_MUTATION - вероятность мутации модели
- NUMBER_OF_MODELS - число моделей в популяции
- EPSILON - необходимая относительная точность на обучающей выборке
В эксперименте на модельных данных была задана функция
при
.
Случайным образом была определена обучающая выборка из 150 объектов. Параметры алгоритма имели значения MODEL_MUTATION = 0.2, NUMBER_OF_MODELS = 150, EPSILON = 0.02.
Результаты работы представлены на графиках:
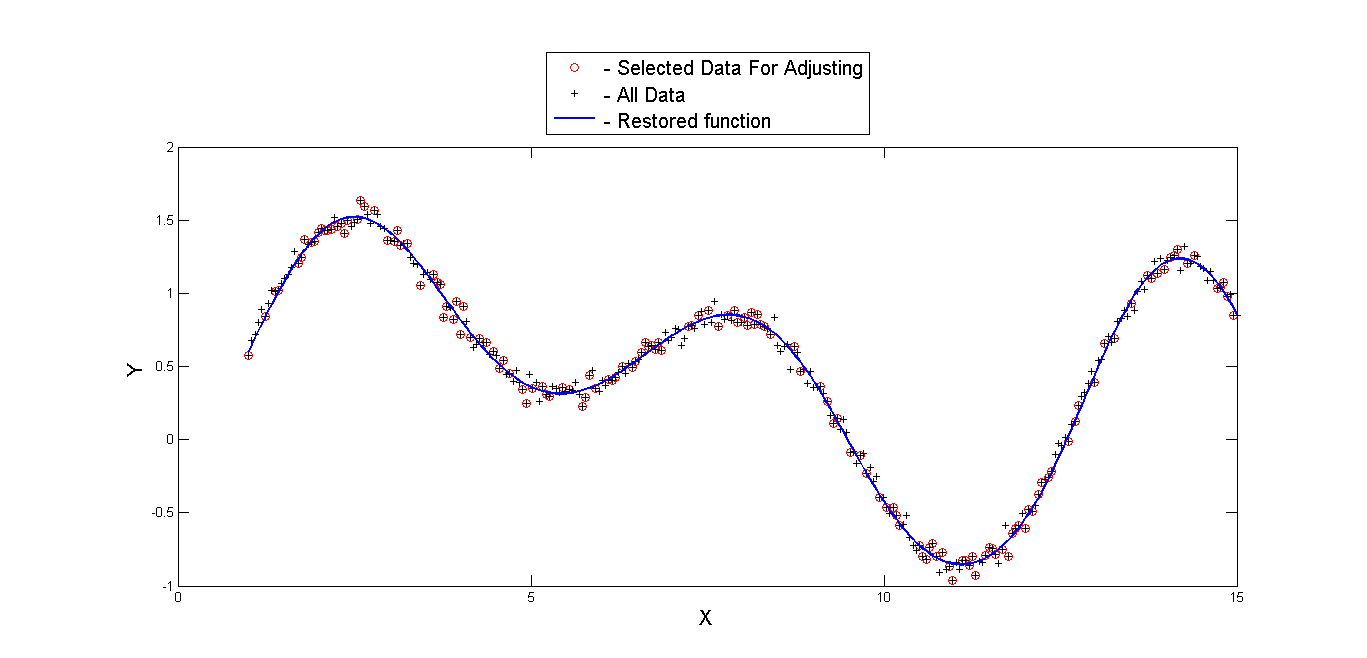 На этом графике изображены обучающая и тестовые выборки, а также график функции, найденной алгоритмом.
На этом графике изображены обучающая и тестовые выборки, а также график функции, найденной алгоритмом.
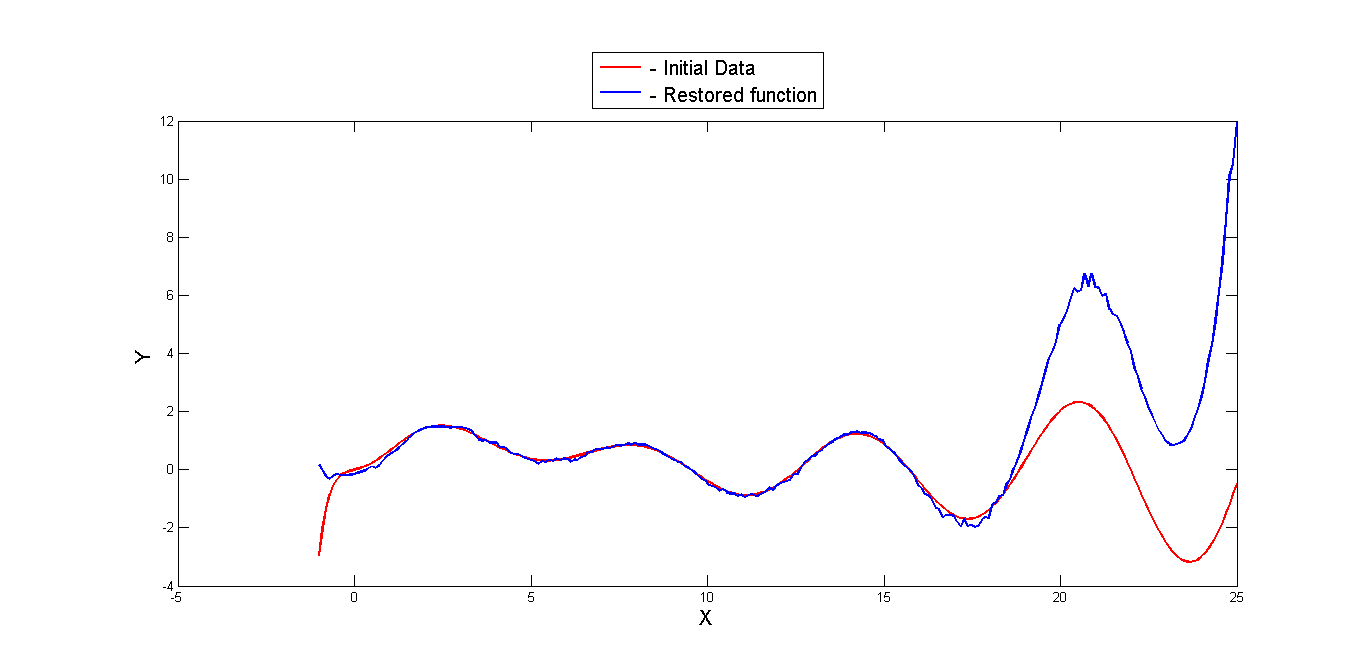
Однако если рассмотреть заданную и найденную функции вне пределов задания выборки, увидим следующий результат :

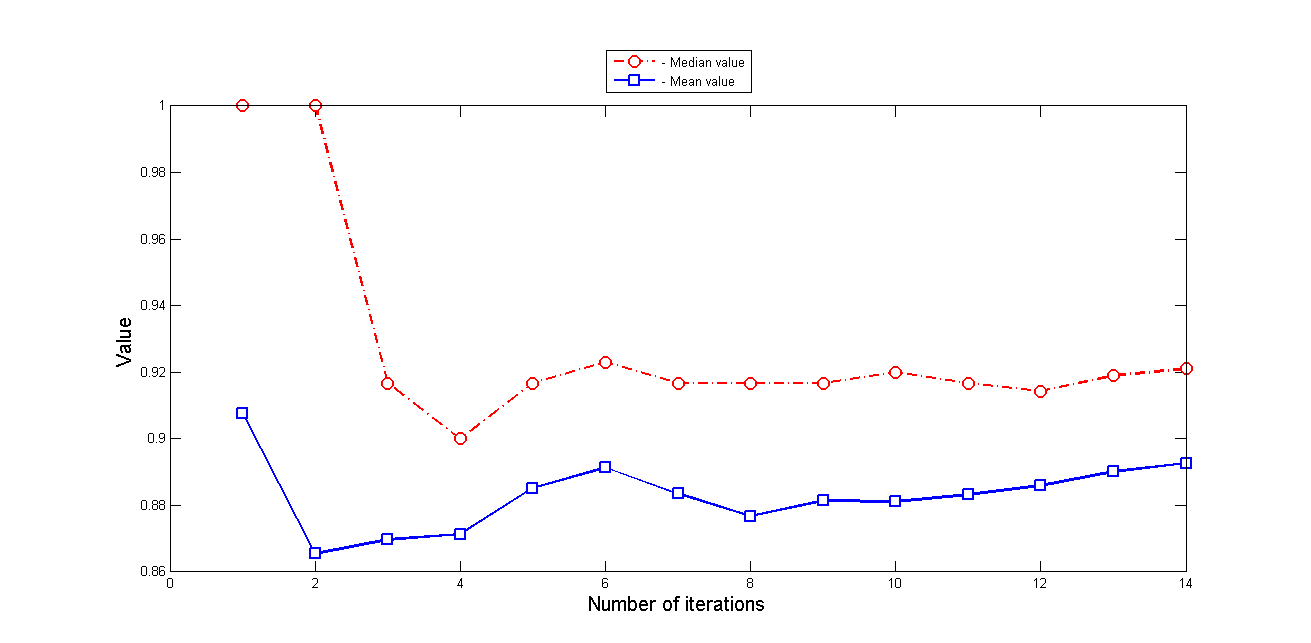
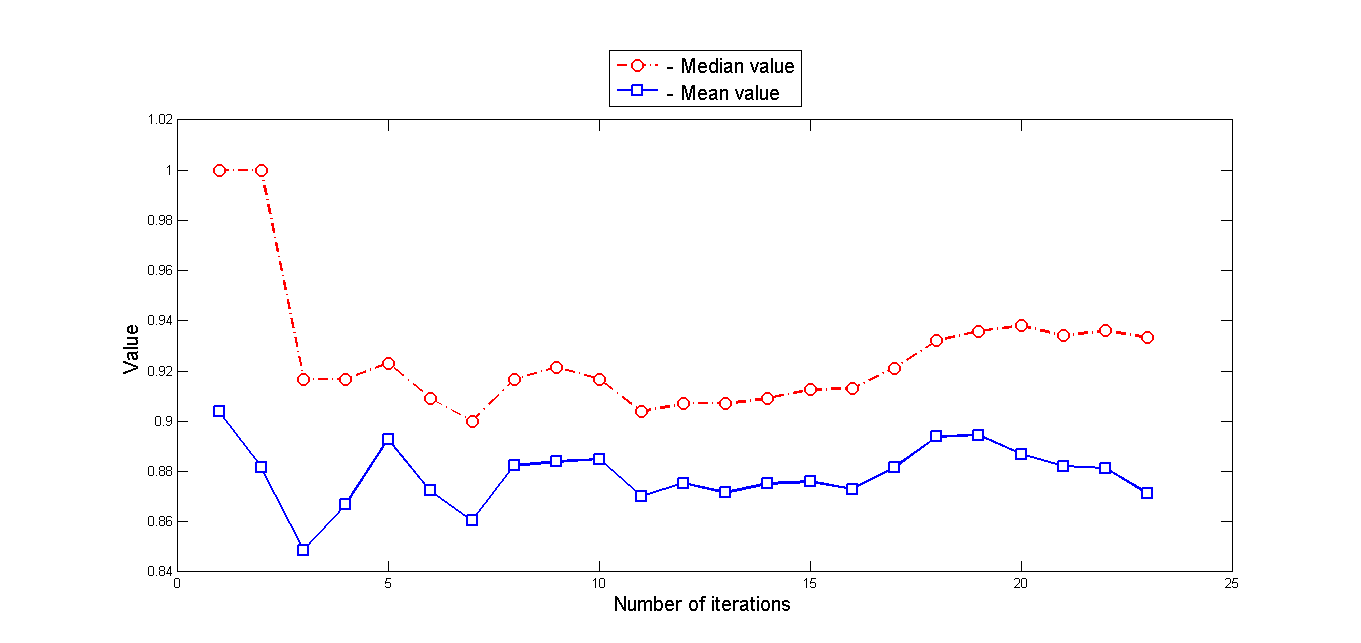
Также исследовались статистические характеристики матрицы попарных расстояний - медиана и среднее значение:
Был проведен и второй эксперимент на модельных данных при большем значении шума в заданной функции и больших требованиях к точности:
была задана функция
и EPSILON = 0.005.
Результаты этого эксперимента:
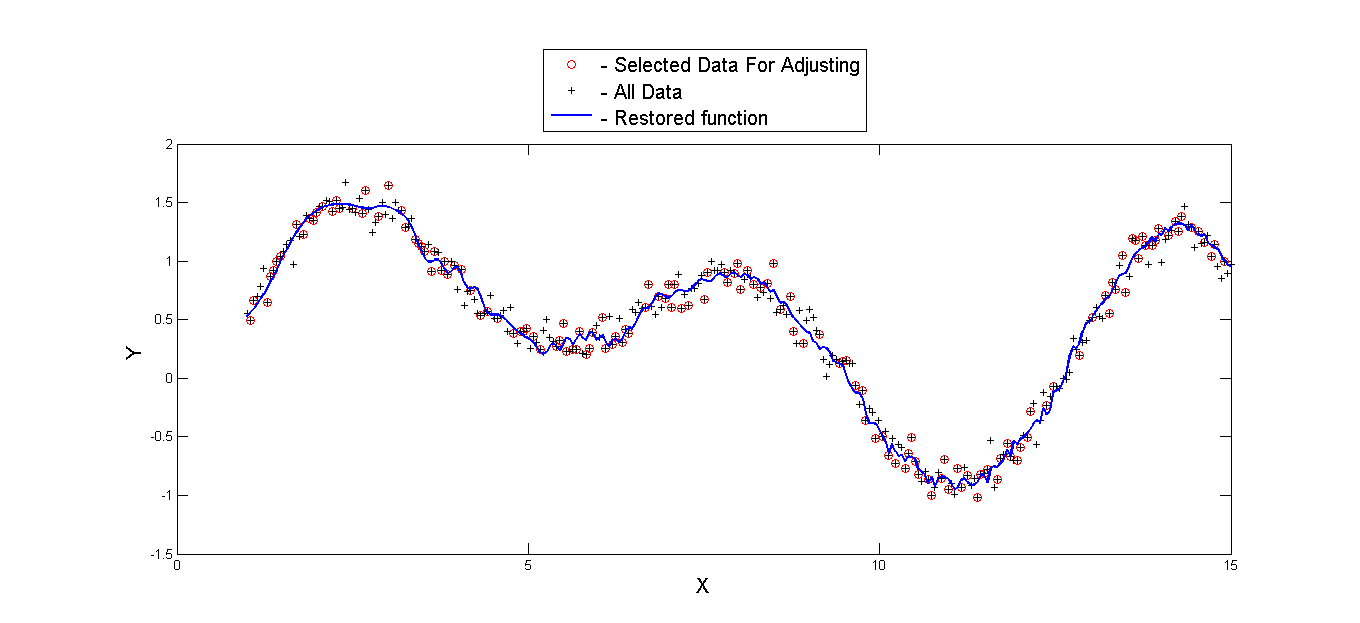
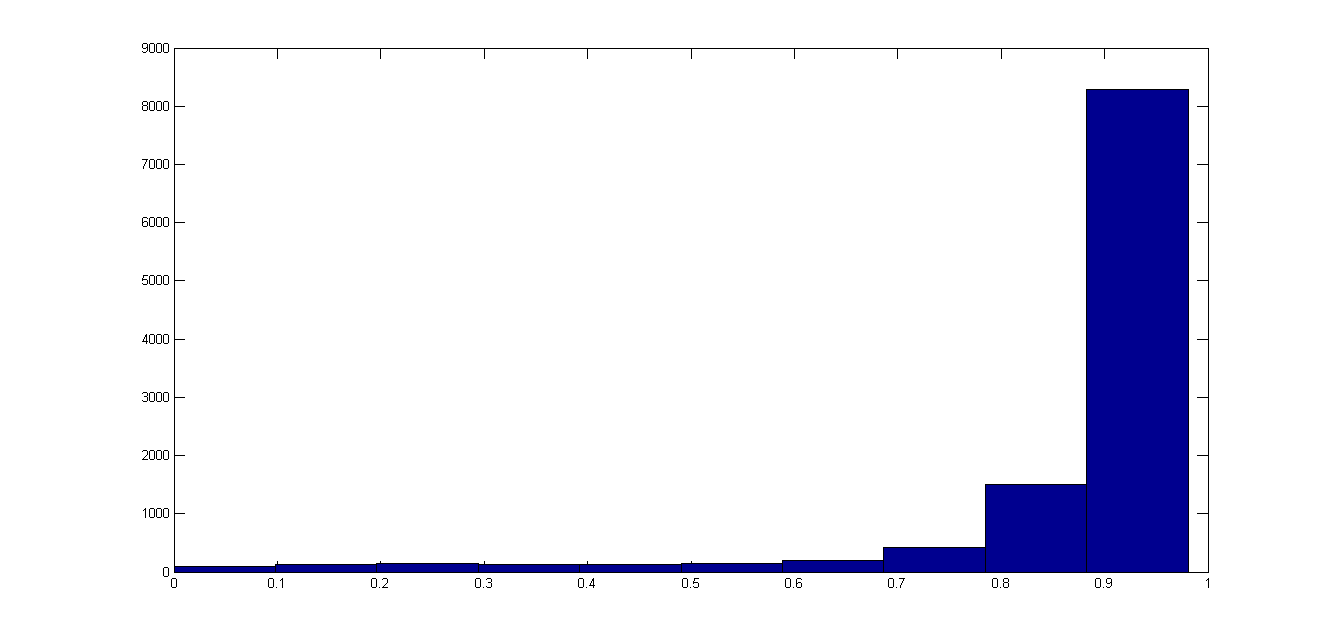
 На следующем рисунке изображена гистограмма значений вектора попарных расстояний на последней итерации.
На следующем рисунке изображена гистограмма значений вектора попарных расстояний на последней итерации.
Литература
- Стрижов В.В. Поиск параметрической регрессионной модели в индуктивно заданном множестве. Журнал вычислительных технологий. 2007. No 1. С. 93-102. [1]
- Макаров Л.И. Метрические свойства функций расстояний между молекулярными графами. Журнал структурной химии. 2007. Том 48. No 2. С.223 - 229.

