Сравнение алгоритмов классификации для кредитного скоринга (отчет)
Материал из MachineLearning.
Введение в проект
Задача кредитного скоринга возникает в банках и в других кредитных организациях при принятии решений о выдаче кредитов. Задача заключается в том, чтобы на основе некоторой информации о заемщике, в данном случае, заполняемая им анкета в банке, обоснованно принять решение — стоит ли ему выдавать кредит, и если да, то на каких условиях.
Описание проекта
Используемые в данном проекте реальные данные «German Credit Data», являются удобным инструментом тестирования различных алгоритмов классификации и их модификаций, а также сравнения их со стандартными алгоритмами.
Цель проекта
Разработка и сравнение алгоритмов классификации для кредитного скоринга.
Обоснование проекта
По полученным результатам можно сделать вывод о том, насколько лучше или хуже разрабатываемый алгоритм классифицирует данные, по сравнению со стандартными алгоритмами, а также насколько целесообразно его использовать.
Описание данных
Данные взяты из репозитория UCI: Statlog (German Credit Data) Data Set . В выборке представлено 1000 объектов. Объектами являются анкеты людей, желавших получить кредит в банке. Изначально анкеты содержали 20 пунктов, таких как состояние банковсого счета заемщика, информация о его кредитной истории, цель займа, величина займа, возраст заемщика, время с момента трудоустройства на текущее место работы и другие. Но так как некоторые из них не были числовыми, а многие алгоритмы (в том числе рассматриваемый в данной статье) работают только с числовыми признаками, то из 20 разнородных признаков было составлено 24 числовых. Ответы — «хорошим» или «плохим» заемщиком оказался человек, получивший кредит. По условию задачи, распознать «плохого» заемщика как «хорошего» в 5 раз хуже, чем «хорошего» как «плохого».
Критерии качества
Внутренним критерием качества служит среднеквадратичная ошибка или критерий максимума логарифма правдоподобия. В данном случае критерии эквивалентны.
Внешними критериями являются взвешенная сумма ошибок классификации
для решающего дерева, а также информационный критерий Акаике (AIC) для алгоритма отбора признаков.
Требования к проекту
Необходимо сравнить рассматриваемые и стандартные алгоритмы классификации по параметрам: стоимость ошибок при обучении, стоимость ошибок на контроле. По данным требуется сделать выводы о работе алгоритмов и условиях в которых лучше применять каждый из них.
Используемые методы
В качестве алгоритма классификации используется бинарное решающее дерево с разделяющими гиперплоскостями в вершинах. Гиперплоскости настраиваются с помощью логистической регрессии, без отбора признаков, либо с помощью LALR (Least Angle Logistic Regression), с отбором признаков.
Постановка задачи
Имеется множество объектов и множество ответов
. Задана обучающая выборка
, где
,
. В данном случае количество объектов
, количество объектов обучающей выборки
и количество признаков
. Задана также функция потерь
в виде матрицы
| | 0 | 1 |
| | 5 | 0 |
Требуется построить алгоритм классификации , который доставляет минимум функционалу качества
Описание алгоритмов
Обзор литературы
Базовые предположения
При построении решающего дерева использовалось предположение о том, что независимые переменные, признаки, имеют множественную корреляцию. Предлагается использовать логистическую регрессионную модель для отыскания разделяющей гиперплоскости.
Математическое описание
Основные понятия
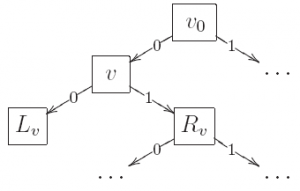
Деревом называется конечный связный граф с множеством вершин , не содержащий циклов и имеющий выделенную вершину
, в которую не входит ни одно ребро. Эта вершина называется корнем дерева. Вершина, не имеющая выходящих ребер, называется терминальной или листом. Обозначим за
множество всех терминальных вершин дерева. Остальные вершины называются внутренними. Дерево называется бинарным, если из любой его внутренней вершины выходит ровно два ребра. Выходящие ребра связывают каждую внутреннюю вершину
с левой дочерней вершиной
и с правой дочерней вершиной
. Каждой внутренней вершине
можно поставить в соответствие некоторый предикат
, а каждой терминальной вершине
можно приписать метку класса
.
Классификация объекта бинарным решающим деревом
При классификации объект проходит по дереву путь от корня до некоторого листа, согласно следующему алгоритму
-
,
- пока вершина
внутренняя
- eсли
то
-
; (переход вправо)
-
- иначе
-
; (переход влево)
-
- вернуть
.
Объект доходит до вершины
тогда и только тогда, когда выполняется конъюнкция
, составленная из всех предикатов, приписанных внутренним вершинам дерева на пути от корня
до вершины
. Множество объектов
, выделяемых терминальными конъюнкциями
, попарно не пересекаются, а их объединение совпадает со всем пространством
.
Отсюда следует, что алгоритм классификации , реализуемый бинарным решающим деревом, можно записать в виде простого голосования конъюнкций:
причем одно и только одно слагаемое во всех этих суммах равно единице.
Построение решающего дерева
В качетсве основного алгоритма использовался рекурсивный алгоритм синтеза бинарного решающего дерева ID3. Работа алгоритма заключается в последовательном дроблении выборки на две части с помощью разделяющей гиперплоскости до тех пор, пока в каждой части не окажутся объекты только одного класса.
Алгоритм построения решающего дерева
Вход:
-
— обучающая выборка;
Выход:
- возвращает корневую вершину дерева,
.
- ПРОЦЕДУРА
;
- eсли все объекты из
лежат в одном классе
то
- создать новый лист
;
-
;
- вернуть
;
- создать новый лист
- найти оптимальные параметры разделяющей гиперплоскости:
-
;
- положить
;
-
- разбить выборку на две части
по предикату
;
- eсли
= ∅ или
= ∅ то
- создать новый лист
;
-
— класс, в котором находится большинство объектов из
;
- создать новый лист
- иначе
- создать новую внутреннюю вершину
;
-
; (построить левое поддерево)
-
; (построить правое поддерево)
- создать новую внутреннюю вершину
- вернуть
Шаг 3 имеет следующую интерпретацию. Для каждой подвыборки принимается модель логистической регрессии, согласно которой, свободные переменные
и зависимая переменная
связаны соотношением
где — вектор весов признаков (направляющий вектор разделяющей гиперплоскости). При ветвлении дерева ищется такой вектор параметров
, который бы доставлял минимум функционалу среднеквадратичной ошибки
Оптимальный вектор параметров находится с помощью метода наименьших квадратов с итеративным пересчётом весов (IRLS), см. также логистическая регрессия (пример).
О сложности
Построенное таким образом дерево может иметь достаточно сложную структуру. В качестве критерия сложности естественно принять количество построенных гиперплоскостей. Чем их больше, тем сложнее структура дерева. Алгоритмы классификации с помощью деревьев различной сложности принадлежат различным алгоритмическим моделям. Обозначим — алгоритм классификации с помощью дерева
сложности
, т.е дерева, содержащего
гиперплоскостей. Некоторое фиксированное дерево
, сложности
, можно свести к дереву
,
, удалив необходимое количество гиперплоскостей. Обозначим
— множество всех алгоритмов классификации с помощью дерева
, полученного из дерева
.
Теперь рассмотрим некоторое бинарное решающее дерево с
гиперплоскостями, построенное согласно вышеуказанному алгоритму. В этом случае
. Если из дерева убрать некоторую терминальную гиперплоскость, сложность уменьшится не единицу. Таким образом, получим некоторое множество
, и т.д. Вся задача состоит в том, чтобы выбрать из множества алгоритмов
алгоритм , доставляющий минимум функционалу качества
:
Варианты или модификации
Описание LALR
Предполагается, что столбцы матрицы объекты-признаки (в матрицу дополнительно включен константный признак) линейно независимы и являются свободными переменными, а зависимая переменная
. Принята модель логистической регрессии, согласно которой
где — вектор весов признаков. Требуется найти для каждого шага LALR вектор весов
доставляющий минимум среднеквадратичной ошибки
Обозначим множество индексов . Для некоторого подмножества
, назовем его активным множеством, определим матрицу активных признаков
где . Определим также матрицы разностей и сумм для некоторого
,
Далее, обозначим
здесь «» означает две разные матрицы, соответствующие «+» и «-».
Теперь полностью опишем алгоритм. Начальное приближение положим . Пусть
текущее приближение функции регрессии. Вектор текущих корреляций имеет вид
Положим
Новое приближение для оценки получаем при добавлении некоторой линейной комбинации выбранных активных признаков
где
«» означает, что минимум берется только из положительных значений. В случае когда
пусто, что соответствует первой итерации,
находится из условия максимума абсолютной корреляции
Таким образом, алгоритм определяет оптимальный признак , обновляет вектор весов
и добавляет новый активный индекс
. В итоге, алгоритм сделает
шагов. На последнем шаге, когда
, веса настраиваются стандартным итерационным МНК с перевзвешиванием элементов (IRLS), как и в логистической регрессии.
Вышеприведенные формулы имеют следующую интерпретацию. На каждом шаге при добавлении нового признака решается задача минимизации среднеквадраничной ошибки, что в нашем случае, эквивалентно максимизации приращения логарифма правдоподобия
решение которой можно выразить в виде .
Применение LALR
Результатом работы алгоритма LALR является последовательность весов признаков . На каждом шаге добавлялся один признак, тем самым увеличивалось на единицу число настраиваемых параметров . Таким образом, получаем последовательность моделей с различным числом параметров. В данной работе, в качестве внешнего критерия выбора модели, использовался информационный критерий Акаике (AIC)
где — число параметров модели, в данном случае, число активных признаков, а
— максимум логарифма правдоподобия. Лучшая модель соответствует минимальному значению критерия Акаике.
Анализ работы LALR на модельных данных
Одним из наиболее простых методов отбора признаков является итеративный алгоритм Forward Stagewise. На каждом шаге алгоритм выбирает признак , имеющий наибольшую корреляцию с текущим вектором остатков
и с достаточно малым по модулю шагом
смещает текущее приближение
в направлении выбранного вектора
,
Чем меньше абсолютная величина шага , тем точнее оценка параметров, но вместе с тем возрастает трудоемкость.
Для сравнения двух алгоритмов мы сгенерировали объектов с 10 независимыми, нормально распределенными признаками
и вектором ответов
, где
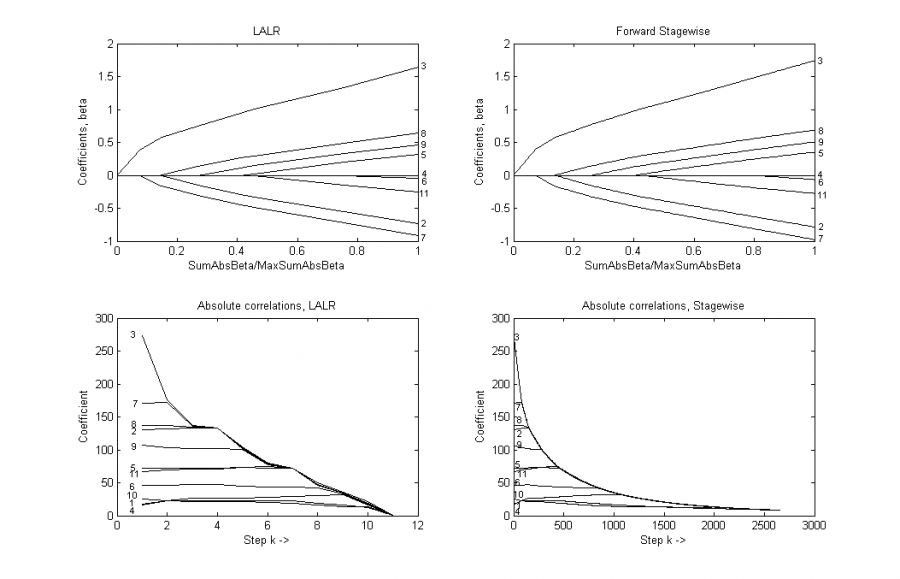
. На рисунке приведены результаты работы алгоритмов LALR и Forward Stagewise.
На первых двух графиках показана зависимость оценок весов от суммы их абсолютных значений
. Каждая ветвь обозначена номером, который соответствует выбранному признаку. Признак с номером 1 является константным. Видно, что последовательности выбираемых признаков совпадают. На нижних графиках приведена зависимость
, абсолютной текущей корреляциии признаков с вектором остатков, от шага
. Номера кривых соответствуют номерам признаков. Из графиков видно, что с ростом
максимум абсолютного значения корреляции монотонно убывает.
Описание системы
- Ссылка на файл system.docs
- Ссылка на файлы системы
Отчет о вычислительных экспериментах
Визуальный анализ работы алгоритма
Анализ качества работы алгоритма
Анализ зависимости работы алгоритма от параметров
Отчет о полученных результатах
Список литературы
| | Данная статья является непроверенным учебным заданием.
До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}. См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |