Метод градиентного спуска
Материал из MachineLearning.
| Строка 7: | Строка 7: | ||
== Метод градиентного спуска == | == Метод градиентного спуска == | ||
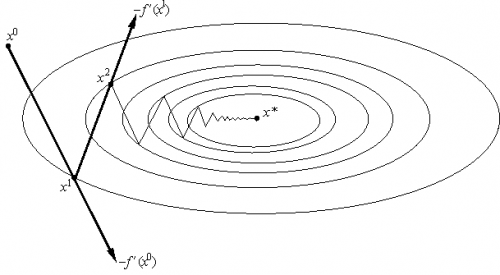
| + | [[Изображение:Grad1.PNG|thumb|500px|Рис.1 Геометрическая интерпретация метода градиентного спуска с постоянным шагом. На каждом шаге мы сдвигаемся по вектору антиградиента, "уменьшенному в <tex>\lambda</tex> раз".]] | ||
=== Идея метода === | === Идея метода === | ||
| Строка 12: | Строка 13: | ||
Основная идея метода заключается в том, чтобы осуществлять оптимизацию в направлении наискорейшего спуска, а это направление задаётся антиградиентом <tex>-\nabla f</tex>: | Основная идея метода заключается в том, чтобы осуществлять оптимизацию в направлении наискорейшего спуска, а это направление задаётся антиградиентом <tex>-\nabla f</tex>: | ||
| - | <tex>x^{[ | + | <tex>x^{[k+1]}=x^{[k]}-\lambda^{[k]}\nabla f(x^{[k]}) </tex> |
| - | где <tex>\lambda^{[ | + | где <tex>\lambda^{[k]}</tex> выбирается |
*постоянной, в этом случае метод может расходиться; | *постоянной, в этом случае метод может расходиться; | ||
*дробным шагом, т.е. длина шага в процессе спуска делится на некое число; | *дробным шагом, т.е. длина шага в процессе спуска делится на некое число; | ||
| - | *наискорейшим спуском: <tex>\lambda^{[ | + | *наискорейшим спуском: <tex>\lambda^{[k]}=\arg\min_{\lambda} \,f(x^{[k]}-\lambda\nabla f(x^{[k]})) </tex> |
=== Алгоритм === | === Алгоритм === | ||
| Строка 25: | Строка 26: | ||
# Повторять: | # Повторять: | ||
| - | # <tex>x^{[ | + | # <tex>x^{[k+1]}=x^{[k]}-\lambda^{[k]}\nabla f(x^{[k]}) </tex>, где <tex>\lambda^{[k]}</tex> выбирается одним из описанных выше способов |
| - | # если выполен критерий останова, то возвращаем текущее значение <tex>x^{[ | + | # если выполен критерий останова, то возвращаем текущее значение <tex>x^{[k+1]}</tex> |
===Критерий останова=== | ===Критерий останова=== | ||
| Строка 37: | Строка 38: | ||
<tex>\eps</tex> - наперед заданное положительное число. | <tex>\eps</tex> - наперед заданное положительное число. | ||
| - | ===Сходимость | + | ===Сходимость градиентного спуска с постоянным шагом=== |
| + | |||
'''Теорема 1 о сходимости метода градиентного спуска спуска с постоянным шагом.''' | '''Теорема 1 о сходимости метода градиентного спуска спуска с постоянным шагом.''' | ||
| Строка 48: | Строка 50: | ||
В условиях теоремы градиентный метод обеспечивает сходимость <tex>\{ x^{[k]} \}</tex> либо к точной нижней грани <tex>\inf_x f(x)</tex> (если функция <tex>f(x)</tex> не имеет минимума) либо к значению <tex>f(x*): \;\lim_{k \to \infty}x^{[k]} = x*,\; f'(x*)=0.</tex> Существуют примеры, когда в точке <tex>x*</tex> реализуется седло, а не минимум. Тем не менее, на практике методы градиентного спуска обычно обходят седловые точки и находят локальные минимумы целевой функции. | В условиях теоремы градиентный метод обеспечивает сходимость <tex>\{ x^{[k]} \}</tex> либо к точной нижней грани <tex>\inf_x f(x)</tex> (если функция <tex>f(x)</tex> не имеет минимума) либо к значению <tex>f(x*): \;\lim_{k \to \infty}x^{[k]} = x*,\; f'(x*)=0.</tex> Существуют примеры, когда в точке <tex>x*</tex> реализуется седло, а не минимум. Тем не менее, на практике методы градиентного спуска обычно обходят седловые точки и находят локальные минимумы целевой функции. | ||
| - | '''Определение.''' Дифференцируемая функция <tex>f</tex> называется сильно выпуклой (с константой <tex> | + | '''Определение.''' Дифференцируемая функция <tex>f</tex> называется сильно выпуклой (с константой <tex>\Lambda>0</tex>), если для любых <tex>x</tex> и <tex>y</tex> из <tex>\mathbb{R}^n</tex> справедливо |
| - | ::<tex>f(x+y)\geq f(x)+ \langle f'(x) ,y \rangle + | + | ::<tex>f(x+y)\geq f(x)+ \langle f'(x) ,y \rangle + \Lambda||y||^2/2 .</tex> |
'''Теорема 2 о сходимости метода градиентного спуска спуска с постоянным шагом.''' | '''Теорема 2 о сходимости метода градиентного спуска спуска с постоянным шагом.''' | ||
| - | Пусть функция <tex>f</tex> дифференцируема, сильно выпукла. Пусть выполняется условие Липшица для градиента <tex>f'(x)</tex>: | + | Пусть функция <tex>f</tex> дифференцируема, сильно выпукла с константой <tex>\Lambda</tex>. Пусть выполняется условие Липшица для градиента <tex>f'(x)</tex>: |
<tex>||f'(x)-f'(y)|| \leq L ||x-y||</tex>. | <tex>||f'(x)-f'(y)|| \leq L ||x-y||</tex>. | ||
Пусть <tex>0<\lambda<2/L</tex>. | Пусть <tex>0<\lambda<2/L</tex>. | ||
| - | Тогда <tex>\lim_{k \to \infty}x^{[k]} = x*, \; ||x^{[k]}-x*||\leq | + | Тогда <tex>\lim_{k \to \infty}x^{[k]} = x*, \; ||x^{[k]}-x*||\leq q^k ||x^{[0]}-x*||, \; q = \max\{|1-\lambda\Lambda|, |1-\lambda L |\}</tex> при любом выборе начального приближения. |
| + | |||
| + | ===Выбор оптимального шага=== | ||
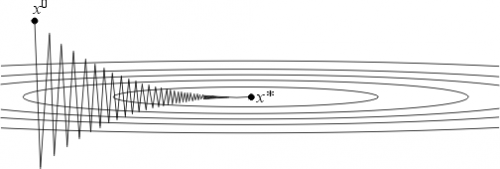
| + | [[Изображение:Grad3.PNG|thumb|500px|Рис.2 Ситуация, когда метод гардиентного спуска сходится плохо.]] | ||
| + | |||
| + | Константа <tex>q</tex>, фигурирующая в теореме 2 и характеризующая скорость сходимости метода, зависит от шага <tex>\lambda</tex>. | ||
| + | Нетрудно видеть, что величина <tex>q=q(\lambda)=\max\{|1-\lambda\Lambda|, |1-\lambda L |\}</tex> минимальна, если шаг <tex>\lambda</tex> выбирается из условия <tex>|1-\lambda\Lambda| = |1-\lambda L |</tex>, т. е. если <tex> \lambda = \lambda* = 2/(\Lambda + L)</tex>. | ||
| + | |||
| + | При таком выборе шага оценка сходимости будет наилучшей и будет характеризоваться величиной: | ||
| + | |||
| + | ::<tex>q=q*=\frac{L-\Lambda}{L+\Lambda}</tex>. | ||
| + | |||
| + | В качестве <tex>\Lambda</tex> и <tex>L</tex> могут выступать равномерные по x оценки сверху и снизу собственных значений оператора <tex>f''(x)</tex>. Если <tex>\lambda << \Lambda</tex>, то <tex>q*\approx 1</tex> и метод сходится очень медленно. Геометрически случай <tex>\lambda << \Lambda</tex> соответствует функциям с сильно вытянутыми линиями уровня (см. рис. 2). Простейшим примером такой функции может служить функция на <tex> \mathbb{R}^2 </tex>, задаваемая формулой: | ||
| + | |||
| + | ::<tex>f(x_1,x_2)=\Lambda x_1^2 + L x_2^2, \; \Lambda << L</tex>. | ||
| + | |||
| + | Поведение итераций градиентного метода для этой функции изображено на рис. 2 — они, быстро спустившись на "дно оврага", затем медленно "зигзагообразно" приближаются к точке минимума. Число <tex>\mu = L/\Lambda </tex> (характеризующее, грубо говоря, разброс собственных значений оператора <tex>f''(x)</tex>) называют числом обусловленности функции <tex>f</tex>. Если <tex>\mu >> 1</tex>, то функции называют плохо обусловленными или овражными. Для таких функций градиентный метод сходится медленно. | ||
| + | |||
| + | Но даже для хорошо обусловленных функций проблема выбора шага нетривиальна в силу отсутствия априорной информации о минимизируемой функции. Если шаг выбирается малым (чтобы гарантировать сходимость), то метод сходится медленно. Увеличение же шага (с целью ускорения сходимости) может привести к расходимости метода. Далее будут описаны два алгоритма автоматического выбора шага, позволяющие частично обойти указанные трудности. | ||
| + | |||
| + | ===Градиентный метод с дроблением шага=== | ||
| + | |||
| + | В этом варианте градиентного метода величина шага <tex>\lambda^{[k]}</tex> на каждой итерации выбирается из условия выполнения неравенства | ||
| + | |||
| + | {{eqno|2}} | ||
| + | ::<tex>f(x^{[k+1]}) = f(x^{[k]}-\lambda^{[k]} f'(x^{[k]})) \leq f(x^{[k]})-\eps \lambda^{[k]}||f'(x^{[k]})||^2 </tex>, | ||
| + | |||
| + | где <tex>\eps \in (0, 1) </tex> - некоторая заранее выбранная константа. | ||
| + | |||
| + | Процедуру нахождения такого <tex>\lambda^{[k]}</tex> обычно оформляют так. Выбирается число <tex>\delta \in (0, 1)</tex> и некоторый начальный шаг <tex>\lambda^{[0]}</tex>. Теперь для каждого k полагают <tex>\lambda^{[k]}=\lambda^{[0]}</tex> и делают шаг градиентного метода. Если с таким <tex>\lambda^{[k]}</tex> условие {{eqref|2}} выполняется, то переходят к следующему k. Если же {{eqref|2}} не выполняется, то умножают <tex>\lambda^{[k]}</tex> на <tex>\delta</tex> ("дробят шаг") и повторяют эту процедуру до тех пор пока неравенство {{eqref|2}} не будет выполняться. В условиях теоремы 1 эта процедура для каждого k за конечное число шагов приводит к нужному <tex>\lambda^{[k]}</tex>. | ||
| + | |||
| + | Можно показать, что в условиях теоремы 2 градиентный метод с дроблением шага линейно сходится. Описанный алгоритм избавляет нас от проблемы выбора <tex>\lambda^{[k]}</tex> на каждом шаге, заменяя ее на проблему выбора параметров <tex> \eps,\;\delta</tex> и <tex>\lambda^{[0]}</tex>, к которым градиентный метод менее чувствителен. При этом, разумеется, объем вычислений возрастает (в связи с необходимостью процедуры дробления шага), впрочем, не очень сильно, поскольку в большинстве задач основные вычислительные затраты ложатся на вычисление градиента. | ||
| + | |||
| + | ===Метод наискорейшего спуска=== | ||
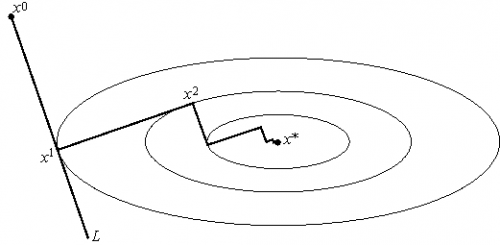
| + | [[Изображение:Grad2.PNG|thumb|500px|Рис.3 Геометрическая интерпретация метода наискорейшего спуска. На каждом шаге <tex>\lambda^{[k]}</tex> выбирается так, чтобы следующая итерация была точкой минимума функции <tex>f</tex> на луче L.]] | ||
| + | |||
| + | Этот вариант градиентного метода основывается на выборе шага из следующего соображения. Из точки <tex>x^{[k]}</tex> будем двигаться в направлении антиградиента до тех пор пока не достигнем минимума функции f на этом направлении, т. е. на луче | ||
| + | <tex>L=\{x=x^{[k]}-\lambda f'(x^{[k]});\; \lambda \leq 0} </tex>: | ||
| + | |||
| + | ::<tex>\lambda^{[k]} = \arg\min_{ \lambda\in [0, \infty)} f(x^{[k]}-\lambda f'(x^{[k]}))</tex>. | ||
| + | |||
| + | Другими словами, <tex>\lambda^{[k]}</tex> выбирается так, чтобы следующая итерация была точкой минимума функции f на луче L (см. рис. 3). Такой вариант градиентного метода называется методом наискорейшего спуска. Заметим, кстати, что в этом методе направления соседних шагов ортогональны. | ||
| + | |||
| + | Метод наискорейшего спуска требует решения на каждом шаге задачи одномерной оптимизации. Практика показывает, что этот метод часто требует меньшего числа операций, чем градиентный метод с постоянным шагом. | ||
| + | |||
| + | В общей ситуации, тем не менее, теоретическая скорость сходимости метода наискорейшего спуска не выше скорости сходимости градиентного метода с постоянным (оптимальным) шагом. | ||
| + | |||
== Числовые примеры == | == Числовые примеры == | ||
== Рекомендации программисту == | == Рекомендации программисту == | ||
| Строка 66: | Строка 114: | ||
== Список литературы == | == Список литературы == | ||
| - | |||
| - | |||
* ''Н.Н.Калиткин.'' Численные методы. Москва «Наука», 1978. | * ''Н.Н.Калиткин.'' Численные методы. Москва «Наука», 1978. | ||
* ''Н.И.Глебов, Ю.А.Кочетов, А.В.Плясунов.'' Методы оптимизации. 2000. | * ''Н.И.Глебов, Ю.А.Кочетов, А.В.Плясунов.'' Методы оптимизации. 2000. | ||
| + | * ''Р.Р.Ахмеров.'' Методы оптимизации гладких функций. | ||
Версия 22:44, 22 ноября 2008
Содержание |
Постановка задачи
Рассмотрим задачу поиска минимума функции , записываемую в виде:
Пусть функция такова, что можно вычислить ее градиент.
Метод градиентного спуска
Идея метода
Основная идея метода заключается в том, чтобы осуществлять оптимизацию в направлении наискорейшего спуска, а это направление задаётся антиградиентом :
где выбирается
- постоянной, в этом случае метод может расходиться;
- дробным шагом, т.е. длина шага в процессе спуска делится на некое число;
- наискорейшим спуском:
Алгоритм
Вход: функция
Выход: найденная точка оптимума
- Повторять:
-
, где
выбирается одним из описанных выше способов
- если выполен критерий останова, то возвращаем текущее значение
Критерий останова
Критерии остановки процесса приближенного нахождения минимума могут быть основаны на различных соображениях. Некоторые из них:
Здеcь - значение, полученное после
-го шага оптимизации.
- наперед заданное положительное число.
Сходимость градиентного спуска с постоянным шагом
Теорема 1 о сходимости метода градиентного спуска спуска с постоянным шагом.
Пусть , функция
дифференцируема, ограничена снизу. Пусть выполняется условие Липшица для градиента
:
.
Пусть
.
Тогда при любом выборе начального приближения.
В условиях теоремы градиентный метод обеспечивает сходимость либо к точной нижней грани
(если функция
не имеет минимума) либо к значению
Существуют примеры, когда в точке
реализуется седло, а не минимум. Тем не менее, на практике методы градиентного спуска обычно обходят седловые точки и находят локальные минимумы целевой функции.
Определение. Дифференцируемая функция называется сильно выпуклой (с константой
), если для любых
и
из
справедливо
Теорема 2 о сходимости метода градиентного спуска спуска с постоянным шагом.
Пусть функция дифференцируема, сильно выпукла с константой
. Пусть выполняется условие Липшица для градиента
:
.
Пусть
.
Тогда при любом выборе начального приближения.
Выбор оптимального шага
Константа , фигурирующая в теореме 2 и характеризующая скорость сходимости метода, зависит от шага
.
Нетрудно видеть, что величина
минимальна, если шаг
выбирается из условия
, т. е. если
.
При таком выборе шага оценка сходимости будет наилучшей и будет характеризоваться величиной:
.
В качестве и
могут выступать равномерные по x оценки сверху и снизу собственных значений оператора
. Если
, то
и метод сходится очень медленно. Геометрически случай
соответствует функциям с сильно вытянутыми линиями уровня (см. рис. 2). Простейшим примером такой функции может служить функция на
, задаваемая формулой:
.
Поведение итераций градиентного метода для этой функции изображено на рис. 2 — они, быстро спустившись на "дно оврага", затем медленно "зигзагообразно" приближаются к точке минимума. Число (характеризующее, грубо говоря, разброс собственных значений оператора
) называют числом обусловленности функции
. Если
, то функции называют плохо обусловленными или овражными. Для таких функций градиентный метод сходится медленно.
Но даже для хорошо обусловленных функций проблема выбора шага нетривиальна в силу отсутствия априорной информации о минимизируемой функции. Если шаг выбирается малым (чтобы гарантировать сходимость), то метод сходится медленно. Увеличение же шага (с целью ускорения сходимости) может привести к расходимости метода. Далее будут описаны два алгоритма автоматического выбора шага, позволяющие частично обойти указанные трудности.
Градиентный метод с дроблением шага
В этом варианте градиентного метода величина шага на каждой итерации выбирается из условия выполнения неравенства
,
где - некоторая заранее выбранная константа.
Процедуру нахождения такого обычно оформляют так. Выбирается число
и некоторый начальный шаг
. Теперь для каждого k полагают
и делают шаг градиентного метода. Если с таким
условие (2) выполняется, то переходят к следующему k. Если же (2) не выполняется, то умножают
на
("дробят шаг") и повторяют эту процедуру до тех пор пока неравенство (2) не будет выполняться. В условиях теоремы 1 эта процедура для каждого k за конечное число шагов приводит к нужному
.
Можно показать, что в условиях теоремы 2 градиентный метод с дроблением шага линейно сходится. Описанный алгоритм избавляет нас от проблемы выбора на каждом шаге, заменяя ее на проблему выбора параметров
и
, к которым градиентный метод менее чувствителен. При этом, разумеется, объем вычислений возрастает (в связи с необходимостью процедуры дробления шага), впрочем, не очень сильно, поскольку в большинстве задач основные вычислительные затраты ложатся на вычисление градиента.
Метод наискорейшего спуска
Этот вариант градиентного метода основывается на выборе шага из следующего соображения. Из точки будем двигаться в направлении антиградиента до тех пор пока не достигнем минимума функции f на этом направлении, т. е. на луче
:
.
Другими словами, выбирается так, чтобы следующая итерация была точкой минимума функции f на луче L (см. рис. 3). Такой вариант градиентного метода называется методом наискорейшего спуска. Заметим, кстати, что в этом методе направления соседних шагов ортогональны.
Метод наискорейшего спуска требует решения на каждом шаге задачи одномерной оптимизации. Практика показывает, что этот метод часто требует меньшего числа операций, чем градиентный метод с постоянным шагом.
В общей ситуации, тем не менее, теоретическая скорость сходимости метода наискорейшего спуска не выше скорости сходимости градиентного метода с постоянным (оптимальным) шагом.
Числовые примеры
Рекомендации программисту
Заключение
Ссылки
Список литературы
- Н.Н.Калиткин. Численные методы. Москва «Наука», 1978.
- Н.И.Глебов, Ю.А.Кочетов, А.В.Плясунов. Методы оптимизации. 2000.
- Р.Р.Ахмеров. Методы оптимизации гладких функций.