м |
м |
| Строка 6: |
Строка 6: |
| | <tex>\sigma_1=\sigma_2=\sigma_3 = 0.01\,:\,0.01\,:\,1,</tex> <br> | | <tex>\sigma_1=\sigma_2=\sigma_3 = 0.01\,:\,0.01\,:\,1,</tex> <br> |
| | <tex>n_1=n_2=n_3=20.</tex> <br> | | <tex>n_1=n_2=n_3=20.</tex> <br> |
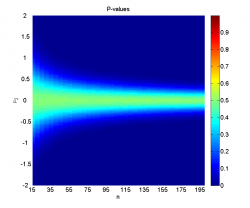
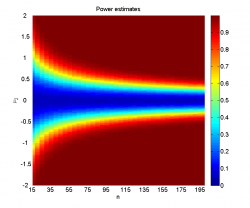
| - | | + | Посмотрим, как от расстояний между выборками и дисперсий зависят средний достигаемый уровень значимости и мощность используемого по умолчанию критерия Фишера: |
| - | | + | <gallery widths="250px" heights="250px"> |
| - | | + | Изображение:3000_p.png|Значения достигаемого уровня значимости, усрёднённого по 3000 экспериментам. |
| - | == Задания ==
| + | Изображение:3000_pow.png|Значения эмпирических оценок мощности критерия при проведении 3000 экспериментов <tex>(\alpha=0.05).</tex> |
| - | === Дисперсионный анализ ===
| + | </gallery> |
| - | Исследовать чувствительность однофакторного дисперсионного анализа и соответствующей процедуры для попарного сравнения средних. <br>
| + | Зависимость выглядит естественно: мощность растёт при увеличении расстояния между выборками и уменьшении дисперсии. |
| - | <tex>x_i^{n_i}, \;\; x_i \sim N(\mu_i, \sigma_i), \;\; i=1,\ldots,m.</tex>
| + | |
| - | | + | |
| - | ::Матвеева: критерий Фишера и процедура Тьюки-Крамера; сравнить результаты применения процедур Тьюки-Крамера и ЛСД.
| + | |
| - | :::<tex>m=3, \;\; \mu_2 = 0, \;\; -\mu_1=\mu_3 = \mu = 0\,:\,0.01\,:\,1, </tex><br><tex> \sigma_1=\sigma_2=\sigma_3 = 0.01\,:\,0.01\,:\,1,\;\; n_1=n_2=n_3=20.</tex> <br>
| + | |
| - | | + | |
| - | ::Игнатьев: критерий Фишера и процедура Тьюки-Крамера.
| + | |
| - | :::<tex>m=3, \;\; \mu_2 = 0, \;\; -\mu_1=\mu_3 = \mu = 0\,:\,0.01\,:\,1, </tex><br><tex> \sigma_1=\sigma_2=\sigma_3 = 1,\;\; n_1=n_3=20, \;\; n_3=10\,:\,5\,:\,100.</tex> <br> | + | |
| - | | + | |
| - | ::Некрасов: критерий Фишера и процедура Тьюки-Крамера.
| + | |
| - | :::<tex>m=3, \;\; \mu_2 = 0, \;\; -\mu_1=\mu_3 = \mu = 0\,:\,0.01\,:\,1, </tex><br><tex> \sigma_1=\sigma_3 = 1,\;\; \sigma_2 = 0.02\,:\,0.02\,:\,2, \;\; n_1=n_3=20, \;\; n_3=10\,:\,5\,:\,100.</tex> <br>
| + | |
| - | | + | |
| - | ::Фигурнов: критерий Фишера и сравнение средних с использованием поправки Бонферрони; сравнить результаты применения поправки Бонферрони и метода ЛСД. | + | |
| - | :::<tex>m=3, \;\; \mu_2 = 0, \;\; -\mu_1=\mu_3 = \mu = 0\,:\,0.01\,:\,1, </tex><br><tex> \sigma_1=\sigma_2=\sigma_3 = 0.01\,:\,0.01\,:\,1,\;\; n_1=n_2=n_3=20.</tex> <br>
| + | |
| - | | + | |
| - | ::Сабурова: критерий Фишера и сравнение средних с использованием поправки Бонферрони. | + | |
| - | :::<tex>m=3, \;\; \mu_2 = 0, \;\; -\mu_1=\mu_3 = \mu = 0\,:\,0.01\,:\,1, </tex><br><tex> \sigma_1=\sigma_3 = 1,\;\; \sigma_2 = 0.02\,:\,0.02\,:\,2, \;\; n_1=n_3=20, \;\; n_3=10\,:\,5\,:\,100.</tex> <br>
| + | |
| - | | + | |
| - | ::Артюхин: критерий Краскела-Уоллиса и метод ЛСД; сравнить результаты применения критериев Краскелла-Уоллиса и Фишера.
| + | |
| - | :::<tex>m=3, \;\; \mu_2 = 0, \;\; -\mu_1=\mu_3 = \mu = 0\,:\,0.01\,:\,1, </tex><br><tex> \sigma_1=\sigma_3 = 1,\;\; \sigma_2 = 0.02\,:\,0.02\,:\,2, \;\; n_1=n_3=20, \;\; n_3=10\,:\,5\,:\,100.</tex> <br>
| + | |
| - | | + | |
| - | ::Бобрик: критерий Краскела-Уоллиса и метод ЛСД; сравнить результаты применения критериев Краскелла-Уоллиса и Фишера.
| + | |
| - | :::<tex>m=3, \;\; \mu_2 = 0, \;\; -\mu_1=\mu_3 = \mu = 0\,:\,0.01\,:\,1, </tex><br><tex> \sigma_1=\sigma_2=\sigma_3 = 1,\;\; n_1=n_3=20, \;\; n_3=10\,:\,5\,:\,100.</tex> <br>
| + | |
| - | | + | |
| - | ::Зимовнов: критерий Джонкхиера и метод ЛСД; сравнить результаты применения критериев Джонкхиера и Краскелла-Уоллиса.
| + | |
| - | :::<tex>m=3, \;\; \mu_2 = 0, \;\; -\mu_1=\mu_3 = \mu = 0\,:\,0.01\,:\,1, </tex><br><tex> \sigma_1=\sigma_2=\sigma_3 = 0.01\,:\,0.01\,:\,1,\;\; n_1=n_2=n_3=20.</tex> <br>
| + | |
| - | | + | |
| - | ::Шанин: критерий Фишера и процедура Тьюки-Крамера.
| + | |
| - | :::<tex>m=2\,:\,1\,:\,30, \;\; \mu_1=0, \;\; \mu_{i} = \mu_{i-1} + \mu, \; i=2,\ldots,m, \;\; \mu = 0\,:\,0.01\,:\,1, </tex><br><tex> \sigma_i=1, \; n_i=20, \; i=1,\ldots,m. </tex>
| + | |
| - | | + | |
| - | ::Полежаев: критерий Краскела-Уоллиса и метод ЛСД; сравнить результаты применения критериев Краскелла-Уоллиса и Фишера.
| + | |
| - | :::<tex>m=2\,:\,1\,:\,30, \;\; \mu_1=0, \;\; \mu_{i} = \mu_{i-1} + 1, \; i=2,\ldots,m</tex><br><tex> \sigma_i=0.02\,:\,0.02\,:\,2, \; n_i=20, \; i=1,\ldots,m. </tex>
| + | |
| - | | + | |
| - | ::Панов: критерий Джонкхиера и метод ЛСД; сравнить результаты применения критериев Джонкхиера и Краскелла-Уоллиса.
| + | |
| - | :::<tex>m=2\,:\,1\,:\,30, \;\; \mu_1=0, \;\; \mu_{i} = \mu_{i-1} + \mu, \; i=2,\ldots,m, \;\; \mu = 0\,:\,0.01\,:\,1, </tex><br><tex> \sigma_i=1, \; n_i=20, \; i=1,\ldots,m. </tex>
| + | |
| - | | + | |
| - | === Множественная проверка гипотез ===
| + | |
| - | Сравнить мощность и корректность процедур множественной проверки гипотез, контролирующих указанную меру числа ошибок второго рода. <br>
| + | |
| - | <tex> x_i^{n}, \;\; x_i \sim N(\mu_i, \sigma_i), \;\; i=1,\ldots,m;</tex><br>
| + | |
| - | <tex> H_i\,:\;\mu_i=0, \;\; H'_i\,:\;\mu_i\neq 0; \;\;</tex> для проверки гипотезы используется [[критерий Стьюдента]],
| + | |
| - | <tex> n=50.</tex>
| + | |
| - | ====FWER====
| + | |
| - | :: Гаврилюк: методы Холма и Шидака,
| + | |
| - | :::<tex> m = 20\,:\,10\,:\,500, \;\; m_0 = 5\,:\,5\,:\,m-5, \;\; FWER\leq\alpha=0.05,</tex> <br>
| + | |
| - | :::<tex> \mu_i \sim N(0.5, 0.1), \; i=1,\ldots,m_0; \;\; \mu_i = 0, \; i=m_0+1,\ldots,m.</tex> <br>
| + | |
| - | | + | |
| - | :: Елшин: методы Холма и Шидака,
| + | |
| - | :::<tex> m = 10\,:\,5\,:\,100, \;\; m_0 = 10, \;\; FWER\leq\alpha=10^{-10:0.5:-1},</tex>
| + | |
| - | :::<tex> \mu_i \sim N(1, 0.1), \; i=1,\ldots,m_0; \;\; \mu_i = 0, \; i=m_0+1,\ldots,m.</tex> <br> | + | |
| - | | + | |
| - | ::Плященко: метод Холма и поправка Бонферрони,
| + | |
| - | :::<tex> m = 100, \;\; m_0 = 5\,:\,:5\,:\,100, \;\; FWER\leq\alpha=10^{-10:0.5:-1},</tex>
| + | |
| - | :::<tex> \mu_1=\ldots=\mu_{m_0} = 0\,:\,0.1\,:\,2, \;\; \mu_i = 0, \; i=m_0+1,\ldots,m.</tex> <br>
| + | |
| - | | + | |
| - | :: Ермушева: метод Холма и поправка Бонферрони,
| + | |
| - | :::<tex> m = 100, \;\; m_0 = 5\,:\,5\,:\,m-5, \;\; FWER\leq\alpha=0.05,</tex>
| + | |
| - | :::<tex> \mu_1=\ldots=\mu_{m_0} = 0\,:\,0.1\,:\,2, \;\; \mu_i = 0, \; i=m_0+1,\ldots,m.</tex> <br>
| + | |
| - | | + | |
| - | :: Марченко: метод Шидака и поправка Бонферрони,
| + | |
| - | :::<tex> m = 10\,:\,5\,:\,100, \;\; m_0 = 10, \;\; FWER\leq\alpha=0.05,</tex>
| + | |
| - | :::<tex> \mu_1=\ldots=\mu_{m_0} = 0\,:\,0.1\,:\,2, \;\; \mu_i = 0, \; i=m_0+1,\ldots,m.</tex> <br>
| + | |
| - | | + | |
| - | | + | |
| - | ====FDR====
| + | |
| - | :: Кириллов: методы Бенджамини-Хохберга и Бенджамини-Иекутиели,
| + | |
| - | :::<tex> m = 20\,:\,10\,:\,500, \;\; m_0 = 5\,:\,5\,:\,m-5, \;\; FDR\leq q=0.05,</tex> <br>
| + | |
| - | :::<tex> \mu_i \sim N(0.5, 0.1), \; i=1,\ldots,m_0; \;\; \mu_i = 0, \; i=m_0+1,\ldots,m.</tex> <br>
| + | |
| - | | + | |
| - | ::Меркулова: методы Бенджамини-Хохберга и Бенджамини-Иекутиели,
| + | |
| - | :::<tex> m = 10\,:\,5\,:\,100, \;\; m_0 = 10, \;\; FDR\leq q=10^{-10:0.5:-1},</tex>
| + | |
| - | :::<tex> \mu_i \sim N(1, 0.1), \; i=1,\ldots,m_0; \;\; \mu_i = 0, \; i=m_0+1,\ldots,m.</tex> <br>
| + | |
| - | | + | |
| - | :: Соколов: метод Бенджамини-Хохберга в чистом виде и с модификацией Стори для оценки <tex>m_0</tex>,
| + | |
| - | :::<tex> m = 20\,:\,10\,:\,500, \;\; m_0 = 5\,:\,5\,:\,m-5, \;\; FDR\leq q=0.05,</tex> <br>
| + | |
| - | :::<tex> \mu_i \sim N(0.5, 0.1), \; i=1,\ldots,m_0; \;\; \mu_i = 0, \; i=m_0+1,\ldots,m.</tex> <br>
| + | |
| - | | + | |
| - | :: Новиков: метод Бенджамини-Хохберга в чистом виде и метод Бенджамини-Иекутиели с модификацией Стори для оценки <tex>m_0</tex>,
| + | |
| - | :::<tex> m = 100, \;\; m_0 = 5\,:\,5\,:\,m-5, \;\; FDR\leq q=0.05,</tex>
| + | |
| - | :::<tex> \mu_1=\ldots=\mu_{m_0} = 0\,:\,0.1\,:\,2, \;\; \mu_i = 0, \; i=m_0+1,\ldots,m.</tex> <br>
| + | |
| - | | + | |
| - | :: Александров: метод Бенджамини-Хохберга в чистом виде и с предварительной процедурой множественной проверки с контролем FDR на уровне <tex>q'</tex> для оценки <tex>m_0</tex>,
| + | |
| - | :::<tex> m = 20\,:\,10\,:\,500, \;\; m_0 = 5\,:\,5\,:\,m-5, \;\; FDR\leq q=0.05,</tex> <br>
| + | |
| - | :::<tex> \mu_1=\ldots=\mu_{m_0} = 0\,:\,0.1\,:\,2, \;\; \mu_i = 0, \; i=m_0+1,\ldots,m.</tex> <br>
| + | |
Исследуем чувствительность однофакторного дисперсионного анализа к расстояниям между выборками и дисперсиям выборок.
, \;\; i=1,\ldots,3,)



Посмотрим, как от расстояний между выборками и дисперсий зависят средний достигаемый уровень значимости и мощность используемого по умолчанию критерия Фишера:
Зависимость выглядит естественно: мощность растёт при увеличении расстояния между выборками и уменьшении дисперсии.