Графические модели (курс лекций)/2012/Задание 1

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
м
м (викификация)
 
Строка 1: Строка 1:
-
[[ГМ|Перейти к основной странице курса]]
+
{{Main|Графические модели (курс лекций)}}
'''Начало выполнения задания''': 29 февраля 2012
'''Начало выполнения задания''': 29 февраля 2012

Текущая версия

Основная статья: Графические модели (курс лекций)

Начало выполнения задания: 29 февраля 2012

Срок сдачи: 7 марта 2012, 18:00


Формулировка задания

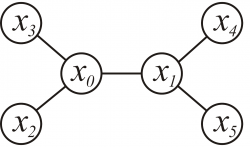
Система соседства марковской сети.
Система соседства марковской сети.

Рассматривается марковская сеть из 6 переменных: x_0, x_1, x_2, x_3, x_4, x_5. Энергия системы задается следующим образом:
E(x_0, \dots, x_5) = \sum_{i = 0}^5 \varphi_i(x_i) + \sum_{(i, j) \in \mathcal{E}} \varphi_{ij}(x_i, x_j).

Множества значений переменных: x_0, x_1 \in \{0, 1 \}; \quad x_2, x_3, x_4, x_5 \in \{0, 1, 2 \}. Система соседства переменных задана на рисунке.

Унарные потенциалы: \varphi_0(x_0) = -5x_0, \quad i = 0; \quad \varphi_i(x_i) = 0, \quad i > 0.

Парные потенциалы: \varphi_{ij}(x_i, x_j) = -|i-j|(x_i - x_j)^2, \quad (i,j) \in \mathcal{E}.

Совместное распределение переменных задается следующим образом:
p(x_0, \dots, x_5) = \frac{1}{Z(T)} \exp\left( -\frac{1}{T} E(x_0, \dots, x_5) \right), где параметр T — температура системы.


Задание:

  1. При помощи алгоритма передачи сообщений вычислить мин-маргиналы и найти все конфигурации, обладающие минимальной энергией.
  2. При помощи алгоритма передачи сообщений вычислить нормировочную константу Z(T) и маргинальные распределения p(x_i) для всех i при температуре T = 1/ln(2).
  3. Как будут меняться маргинальные распределения при изменении температуры? Ответ обосновать.


Оформление задания

Выполненный вариант задания необходимо сдать лектору в бумажном виде или прислать на bayesml@gmail.com в электронном виде. Для решения задания можно использовать собственноручно написанные программные средства. Если таковые используются, то их тоже необходимо прислать.

Источник — «http://poligon.machinelearning.ru/wiki/index.php?title=%D0%93%D1%80%D0%B0%D1%84%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5_%D0%BC%D0%BE%D0%B4%D0%B5%D0%BB%D0%B8_%28%D0%BA%D1%83%D1%80%D1%81_%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D0%B9%29/2012/%D0%97%D0%B0%D0%B4%D0%B0%D0%BD%D0%B8%D0%B5_1»