Критерий хи-квадрат

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(→Определение)
(→Проверка гипотезы)
Строка 28: Строка 28:
== Проверка гипотезы ==
== Проверка гипотезы ==
 +
[[Изображение:Chi-square.png|280px|thumb|Распределение хи-квадрат]]
 +
В зависимости от значения критерия <tex>\chi^2</tex>, может выполняться одна из гипотез:
* гипотеза неслучайности
* гипотеза неслучайности
 +
<tex>\chi^2_1 < \chi^2 < \chi^2_2</tex>, гипотеза <tex>H_0</tex> выполняется.
 +
* гипотеза случайности
* гипотеза случайности
 +
<tex>\chi^2 \leq \chi^2_1</tex> (попадает в левый "хвост" распределения) гипотеза <tex>H_0</tex> отвергается.
 +
* гипотеза согласия
* гипотеза согласия
 +
<tex>\chi^2 \geq \chi^2_1</tex> (попадает в левый "хвост" распределения) гипотеза <tex>H_0</tex> отвергается.
== Сложная гипотеза ==
== Сложная гипотеза ==

Версия 11:18, 7 декабря 2008

Содержание

Статья в настоящий момент дорабатывается.
Венжега Андрей 00:08, 14 ноября 2008 (MSK)


Определение

Пусть дана случайная величина X .

Гипотеза H_0 : с. в. X подчиняется закону распределения F(x).


Для проверки гипотезы рассмотрим выборку, состоящую из n независимых наблюдений над с.в. X: X^n = \left( x_1, \cdots \x_n \right), \; x_i \in \left[ a, b \right], \; \forall i=1 \dots n . По выборке построим эмпирическое распределение F^*(x) с.в X. Сравнение эмпирического F^*(x) и теоретического распределения F(x) производится с помощью специально подобранной случайной величины — критерия согласия. Рассмотрим критерий согласия Пирсона (критерий \chi^2):


Гипотеза H_0^* : Хn порождается функцией F^*(x).

Разделим [a,b] на k непересекающихся интервалов (a_i, b_i], \; i=1 \dots k;

Пусть n_j - количество наблюдений в j-м интервале: n_j = \sum_{i=1}^n \left[ a_i <x \leq b_i \right] ;

p_j = F(b_j)-F(a_j) - вероятность попадания наблюдения в j-ый интервал при выполнении гипотезы H_0^* ;

E_j = np_j Ожидаемое число попаданий в j-ый интервал;

Статистика: \chi^2 = \sum_{i=1}^k \frac{ \left( n_j-E_j \right)^2}{E_j} \sim \chi_{k-1}^2 - Распределение хи-квадрат с k-1 степенью свободы.

Критерий \chi^2 - наиболее часто используемый статистический критерй для проверки гипотезы H_0, что наблюдаемая случайная величина подчиняется некому теоретическому закону распределению.

Проверка гипотезы

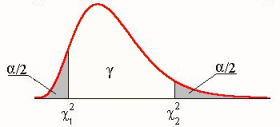
Распределение хи-квадрат
Распределение хи-квадрат

В зависимости от значения критерия \chi^2, может выполняться одна из гипотез:

  • гипотеза неслучайности

\chi^2_1 < \chi^2 < \chi^2_2, гипотеза H_0 выполняется.

  • гипотеза случайности

\chi^2 \leq \chi^2_1 (попадает в левый "хвост" распределения) гипотеза H_0 отвергается.

  • гипотеза согласия

\chi^2 \geq \chi^2_1 (попадает в левый "хвост" распределения) гипотеза H_0 отвергается.

Сложная гипотеза

Теорема Фишера

Литература

Ссылки

[Критерий хи-квадрат (en.wiki)]

Источник — «http://poligon.machinelearning.ru/wiki/index.php?title=%D0%9A%D1%80%D0%B8%D1%82%D0%B5%D1%80%D0%B8%D0%B9_%D1%85%D0%B8-%D0%BA%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82»
Личные инструменты