Графические модели (курс лекций)/2013/Задание 2
Материал из MachineLearning.
м (→Рекомендации по выполнению задания) |
м |
||
| Строка 12: | Строка 12: | ||
Среда для выполнения задания — MATLAB. | Среда для выполнения задания — MATLAB. | ||
| - | == [http:// | + | == [http://ru.wikipedia.org/wiki/LDPC Низкоплотностные коды] == |
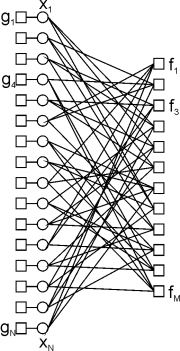
[[Image:GM13_task2_fg.png|thumb|Фактор-граф для (16,4)-низкоплотностного кода, в проверочной матрице которого в каждом столбце по 3 единицы, а в каждой строке - по 4 единицы.]] | [[Image:GM13_task2_fg.png|thumb|Фактор-граф для (16,4)-низкоплотностного кода, в проверочной матрице которого в каждом столбце по 3 единицы, а в каждой строке - по 4 единицы.]] | ||
| Строка 31: | Строка 31: | ||
Восстановление кодового слова <tex>x</tex> по полученному слову <tex>y</tex> предлагается осуществлять как | Восстановление кодового слова <tex>x</tex> по полученному слову <tex>y</tex> предлагается осуществлять как | ||
| - | <tex>x_n^* = \arg\max p(x_n|y)</tex>, а маргинальные распределения <tex>p(x_n|y)</tex> оценивать в помощью циклического алгоритма передачи сообщений (sum-product loopy BP) на фактор-графе. При этом для упрощения алгоритма декодирования предлагается избавиться от факторов-унарных потенциалов (путем их включения в сообщения от переменных <tex>x_n</tex> к факторам <tex>f_m</tex>), а в качестве расписания пересчёта сообщений выбрать параллельное расписание, при котором сначала все переменные одновременно посылают сообщения во все факторы, а затем все факторы одновременно посылают сообщения во все вершины. Детали алгоритма передачи сообщений, в том числе, эффективные формулы для пересчета сообщений от факторов к вершинам можно найти в [http://www.inference.phy.cam.ac.uk/mackay/itila/book.html книге МакКая] (стр. 560-561). | + | <tex>x_n^* = \arg\max p(x_n|y)</tex>, а маргинальные распределения <tex>p(x_n|y)</tex> оценивать в помощью циклического алгоритма передачи сообщений (sum-product loopy BP) на фактор-графе. При этом для упрощения алгоритма декодирования предлагается избавиться от факторов-унарных потенциалов (путем их включения в сообщения от переменных <tex>x_n</tex> к факторам <tex>f_m</tex>), а в качестве расписания пересчёта сообщений выбрать параллельное расписание, при котором сначала все переменные одновременно посылают сообщения во все факторы, а затем все факторы одновременно посылают сообщения во все вершины. Детали алгоритма передачи сообщений, в том числе, эффективные формулы для пересчета сообщений от факторов к вершинам можно найти [http://ru.wikipedia.org/wiki/Код_с_малой_плотностью_проверок_на_чётность#Декодирование здесь], а также в [http://www.inference.phy.cam.ac.uk/mackay/itila/book.html книге МакКая] (стр. 560-561). |
== Формулировка задания == | == Формулировка задания == | ||
Версия 16:37, 2 марта 2013
| | Формулировка задания находится в стадии разработки. Убедительная просьба не приступать к выполнению задания до тех пор, пока это предупреждение не будет удалено. |
Начало выполнения задания: 3 марта 2013 г.
Срок сдачи: 17 марта 2013 г., 23:59.
Среда для выполнения задания — MATLAB.
Низкоплотностные коды
Низкоплотностный код (или код с малой плотностью проверок на чётность) представляет собой (N,K)-бинарный линейный блоковый код, в котором проверочная матрица является сильно разреженной. Таким образом, вектор
является кодовым словом, если
(здесь и далее все вычисления проводятся по модулю 2).
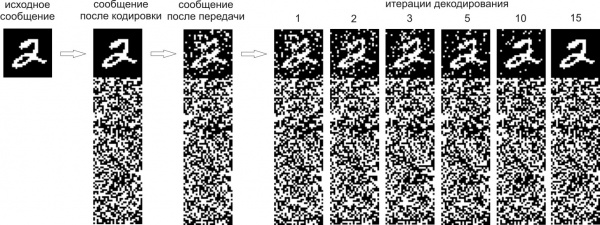
Рассмотрим бинарный симметричный канал для передачи данных. Здесь при передаче каждый бит независимо инвертируется с некоторой вероятностью q. Таким образом, бинарный симметричный канал задает распределение для передаваемого кодового слова
и полученного на выходе слова
как
.
Пропускная способность данного канала определяется величиной .
Объединяя низкоплотностный код с бинарным симметричным каналом, получаем следующую вероятностную модель для пары :
.
Здесь M=N-K — количество проверок на чётность, — m-ая строка матрицы H, а
— индикаторная функция. Фактор-граф введённой модели показан на рис. справа.
Восстановление кодового слова по полученному слову
предлагается осуществлять как
, а маргинальные распределения
оценивать в помощью циклического алгоритма передачи сообщений (sum-product loopy BP) на фактор-графе. При этом для упрощения алгоритма декодирования предлагается избавиться от факторов-унарных потенциалов (путем их включения в сообщения от переменных
к факторам
), а в качестве расписания пересчёта сообщений выбрать параллельное расписание, при котором сначала все переменные одновременно посылают сообщения во все факторы, а затем все факторы одновременно посылают сообщения во все вершины. Детали алгоритма передачи сообщений, в том числе, эффективные формулы для пересчета сообщений от факторов к вершинам можно найти здесь, а также в книге МакКая (стр. 560-561).
Формулировка задания
- Реализовать алгоритм построения по заданной проверочной матрице чётности H порождающей матрицы кода G для систематического кодирования;
- Реализовать алгоритм декодирования низкоплотностного кода на основе loopy BP, провести временные замеры реализованного алгоритма для различных значений входных параметров, время работы алгоритма не должно превышать XX секунд для ...
- Реализовать алгоритм оценки вероятности битовой и блоковой ошибки кода с помощью метода стат. испытаний (многократная случайная генерация слова
, его преобразование к кодовому слову
, передача по каналу с независимым инвертированием каждого бита с заданной вероятностью
, восстановление кодового слова
с помощью алгоритма декодирования и подсчет необходимых характеристик);
- Провести эксперименты по оцениванию битовой и блоковой ошибки низкоплотностного кода для различных значений длины кодового слова N, скорости кода R, вероятности инвертирования бита при передаче по каналу связи q и среднего количества единиц в столбце проверочной матрицы j. В частности, необходимо проанализировать следующие ситуации:
- Теорема Шеннона определяет пропускную способность канала как максимально допустимую скорость кода, при которой возможно осуществление надежной коммуникации. Требуется проверить, как меняются характеристики кода при изменении скорости R от минимального значения до пропускной способности канала.
- Теорема Шеннона предполагает, что качество кода растет при увеличении длины кодового слова N. Требуется проверить это предположение.
- Одно из следствий теоремы Шеннона утверждает, что хорошими кодами являются коды со случайной проверочной матрицей H. В частности, здесь предполагается, что качество кода должно расти при увеличении среднего количества единиц в столбце проверочной матрицы j. Требуется проверить это утверждение для низкоплотностных кодов.
Рекомендации по выполнению задания
1. Разреженную проверочную матрицу кода заданных размеров можно строить с помощью случайной генерации (с соблюдением условия полноранговости). Однако, здесь рекомендуется воспользоваться готовой реализацией, которая генерирует проверочную матрицу с заданным количеством единиц в каждом столбце. При этом реализованный алгоритм старается сократить количество циклов длины 4 в генерируемой матрице, т.к. наличие коротких циклов в графе, как правило, значительно усложняет работу алгоритма loopy BP.
2. Одним из способов построения порождающей матрицы кода по заданной проверочной матрице является преобразование проверочной матрицы к каноническому ступенчатому виду. Такое преобразование может быть сделано с помощью гауссовских исключений. При выполнении задания разрешается пользоваться сторонними кодами по реализации стандартных алгоритмов линейной алгебры (с соответствующими указаниями в отчёте). Однако, рекомендуется реализовывать алгоритм гауссовских исключений в логике по модулю 2 самостоятельно, т.к. такая реализация может быть сделана значительно эффективнее по сравнению с общим случаем логики по модулю произвольного простого числа, т.к. в логике по модулю два нет необходимости использовать операцию деления и, например, искать ведущий элемент при очередном вычитании (т.к. все ненулевые элементы равны единице).
3. Алгоритм декодирования удобно реализовывать в т.н. синдромном представлении. Полученное на выходе канала слово можно представить как
, где
— посылаемое кодовое слово, а
— вектор ошибок, которые вносит канал. Назовём величину
синдромом полученного сообщения. Тогда
, и на этапе декодирования можно вместо
оценивать вектор ошибок
путем оценки аргмаксимумов маргинальных распределений
в вероятностной модели
.
Зная , искомое кодовое слово можно найти как
. Заметим, что реализация алгоритма декодирования в синдромном представлении избавляет от необходимости предварительной реализации алгоритма кодирования.
4. В эффективной реализации алгоритма декодирования все вычисления на очередной итерации не должны использовать вложенных циклов.
Оформление задания
Выполненное задание следует отправить письмом по адресу bayesml@gmail.com с заголовком письма «[ГМ13] Задание 2 <ФИО>». Убедительная просьба присылать выполненное задание только один раз с окончательным вариантом. Также убедительная просьба строго придерживаться заданных ниже прототипов реализуемых функций.
Присланный вариант задания должен содержать в себе:
- Текстовый файл в формате PDF с указанием ФИО, содержащий описание всех проведенных исследований. Данный файл должен, в частности, содержать необходимые графики зависимости битовой и блоковой ошибки кода в зависимости от различных значений параметров.
- Все исходные коды с необходимыми комментариями.
| Построение порождающей матрицы для систематического кодирования | ||
|---|---|---|
| [G, ind] = ldpc_gen_matrix(H) | ||
| ВХОД | ||
| ||
| ВЫХОД | ||
|
| Алгоритм декодирования LDPC-кода в синдромном представлении | ||||||||
|---|---|---|---|---|---|---|---|---|
| [e, status] = ldpc_decoding(z, H, q, param_name1, param_value1, ...) | ||||||||
| ВХОД | ||||||||
| ||||||||
| ВЫХОД | ||||||||
|
| Оценка характеристик LDPC-кода с помощью метода Монте Карло | ||||
|---|---|---|---|---|
| [err_bit, err_block, diver] = ldpc_mc(H, G, q, num_points) | ||||
| ВХОД | ||||
| ||||
| ВЫХОД | ||||
|