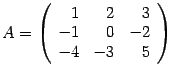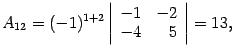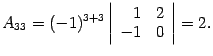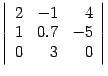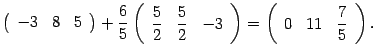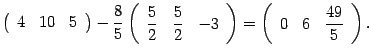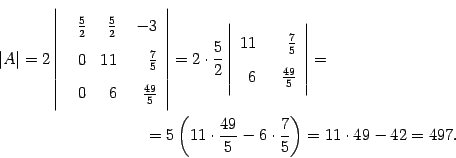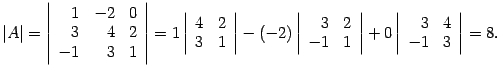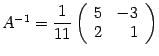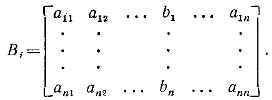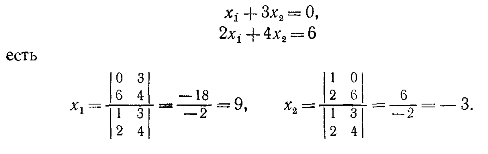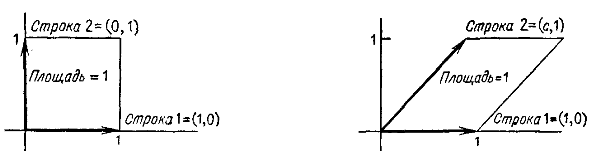Вычисление определителя
Материал из MachineLearning.
(→Определитель) |
(замечание потеряло актуальность) |
||
| (17 промежуточных версий не показаны.) | |||
| Строка 1: | Строка 1: | ||
| - | |||
| - | |||
| - | |||
| - | |||
== Постановка задачи == | == Постановка задачи == | ||
| - | Задание подразумевает знакомство пользователя с основными понятиями численных методов, такими как определитель и обратная матрица, и различными способами их вычислений. В данном теоретическом отчете простым и доступным языком сначала вводятся основные понятия и определения, на основании которых проводится дальнейшее исследование. Пользователь может не иметь специальных знаний в области численных методов и линейной алгебры, но с легкостью сможет воспользоваться результатами данной работы. Для наглядности приведена программа вычисления определителя матрицы несколькими методами, написанная на языке программирования C++. Программа используется как лабораторный стенд для создания иллюстраций к отчету. А также проводится исследование методов для решения систем линейных алгебраических уравнений. Доказывается бесполезность вычисления обратной матрицы, поэтому в работе приводится | + | Задание подразумевает знакомство пользователя с основными понятиями численных методов, такими как [[определитель]] и [[обратная матрица]], и различными способами их вычислений. В данном теоретическом отчете простым и доступным языком сначала вводятся основные понятия и определения, на основании которых проводится дальнейшее исследование. Пользователь может не иметь специальных знаний в области [[Численные методы|численных методов]] и [[Линейная алгебра|линейной алгебры]], но с легкостью сможет воспользоваться результатами данной работы. Для наглядности приведена программа вычисления определителя матрицы несколькими методами, написанная на языке программирования C++. Программа используется как лабораторный стенд для создания иллюстраций к отчету. А также проводится исследование методов для решения [[Система линейных алгебраических уравнений|систем линейных алгебраических уравнений]]. Доказывается бесполезность вычисления обратной матрицы, поэтому в работе приводится более оптимальные способы решения уравнений не вычисляя ее. Рассказывается почему существует такое количество различных методов вычисления определителей и обратных матриц и разбираются их недостатки. Также рассматриваются погрешности при вычислении определителя и оценивается достигнутая точность. Помимо русских терминов в работе используются и их английские эквиваленты для понимания, под какими названиями искать численные процедуры в библиотеках и что означают их параметры. |
== Основные определения и простейшие свойства == | == Основные определения и простейшие свойства == | ||
| Строка 81: | Строка 77: | ||
'''Следствие.''' Определитель единичной матрицы равен единице, <tex> |E| = 1 </tex>. | '''Следствие.''' Определитель единичной матрицы равен единице, <tex> |E| = 1 </tex>. | ||
| + | |||
'''Вывод.''' Перечисленные выше свойства позволяют находить определители матриц достаточно высоких порядков при сравнительно небольшом объеме вычислений. Алгоритм вычислений следующий. | '''Вывод.''' Перечисленные выше свойства позволяют находить определители матриц достаточно высоких порядков при сравнительно небольшом объеме вычислений. Алгоритм вычислений следующий. | ||
'''Алгоритм создания нулей в столбце.''' | '''Алгоритм создания нулей в столбце.''' | ||
| - | Пусть требуется вычислить определитель <tex> A </tex> порядка <tex> n </tex>. Если <tex> a_{11} </tex>, то поменяем местами первую строку и любую другую, в которой первый элемент не нуль. В результате определитель <tex> A </tex>, будет равен определителю новой матрицы с противоположным знаком. Если же первый элемент каждой строки равен нулю, то матрица <tex> A </tex> имеет нулевой столбец и по утверждениям 1, 13 ее определитель равен нулю. | + | Пусть требуется вычислить определитель <tex> A </tex> порядка <tex> n </tex>. Если <tex> a_{11}=0</tex>, то поменяем местами первую строку и любую другую, в которой первый элемент не нуль. В результате определитель <tex> A </tex>, будет равен определителю новой матрицы с противоположным знаком. Если же первый элемент каждой строки равен нулю, то матрица <tex> A </tex> имеет нулевой столбец и по утверждениям 1, 13 ее определитель равен нулю. |
Итак, считаем, что уже в исходной матрице <tex> a_{11} \neq 0 </tex>. Первую строку оставляем без изменений. Прибавим ко второй строке первую строку, умноженную на число <tex> (-\frac{a_{21}}{a_{11}}) </tex>. Тогда первый элемент второй строки будет равен [[Изображение:17.png]]. | Итак, считаем, что уже в исходной матрице <tex> a_{11} \neq 0 </tex>. Первую строку оставляем без изменений. Прибавим ко второй строке первую строку, умноженную на число <tex> (-\frac{a_{21}}{a_{11}}) </tex>. Тогда первый элемент второй строки будет равен [[Изображение:17.png]]. | ||
| Строка 130: | Строка 127: | ||
=== Обратная матрица === | === Обратная матрица === | ||
| + | '''Определение 3.''' Матрица <tex> B </tex> называется ''обратной матрицей'' для квадратной матрицы <tex> A </tex>, если <tex> AB = BA = E </tex>. | ||
| + | |||
| + | Из определения следует, что обратная матрица <tex> B </tex> будет квадратной матрицей того же порядка, что и матрица <tex> A </tex>(иначе одно из произведений <tex> AB </tex> или <tex> BA </tex> было бы не определено). | ||
| + | |||
| + | Обратная матрица для матрицы <tex> A </tex> обозначается <tex> A^{-1} </tex>. Таким образом, если <tex> A^{-1} </tex> существует, то <tex> AA^{-1} = A^{-1}A = E </tex>. | ||
| + | |||
| + | Из определения обратной матрицы следует, что матрица <tex> A </tex> является обратной для матрицы <tex> A^{-1} </tex>, то есть <tex> (A^{-1})^{-1} = A </tex>. Про матрицы <tex> A </tex> и <tex> A^{-1} </tex> можно говорить, что они обратны друг другу или взаимно обратны. | ||
| + | |||
| + | '''Если определитель матрицы равен нулю, то обратная к ней не существует.''' | ||
| + | |||
| + | Так как для нахождения обратной матрицы важно, равен ли определитель марицы нулю или нет, то введем следующие определения. | ||
| + | |||
| + | |||
| + | '''Определение 4.''' Квадратную матрицу <tex> A </tex> назовем ''вырожденной'' или ''особенной матрицей'', если <tex> |A| = 0 </tex>, и ''невырожденной'' или ''неособенной матрицей'', если <tex> |A| \neq 0 </tex>. | ||
| + | |||
| + | '''Утверждение.''' Если обратная матрица существует, то она единственна. | ||
| + | |||
| + | '''Утверждение.''' Если квадратная матрица <tex> A </tex> является невырожденной, то обратная для нее существует и [[Изображение:32.png]] (1) | ||
| + | где <tex> A_{ij} </tex> - алгебраические дополнения к элементам <tex> a_{ij} </tex>. | ||
| + | |||
| + | '''Теорема.''' | ||
| + | Обратная матрица для квадратной матрицы <tex> A </tex> существует тогда и только тогда, когда матрица <tex> A </tex> - невырожденная, обратная матрица единственна, и справедлива формула (1). | ||
| + | |||
| + | '''Замечание.''' Следует обратить особое внимание на места, занимаемые алгебраическими дополнениями в формуле обратной матрицы: первый индекс показывает номер '''столбца''', а второй - номер '''строки''', в которые нужно записать вычисленное алгебраическое дополнение. | ||
| + | |||
| + | '''Пример.''' Найдите обратную матрицу для матрицы [[Изображение:33.png]]. | ||
| + | |||
| + | '''Решение.''' Находим определитель [[Изображение:34.png]] | ||
| + | |||
| + | Так как <tex> |A| \neq 0 </tex>, то матрица <tex> A </tex> - невырожденная, и обратная для нее существует. | ||
| + | Находим алгебраические дополнения: [[Изображение:35.png]] | ||
| + | |||
| + | Составляем обратную матрицу, размещая найденные алгебраические дополнения так, чтобы первый индекс соответствовал столбцу, а второй - строке: [[Изображение:36.png]] (2) | ||
| + | |||
| + | Полученная матрица (2) и служит ответом к задаче. | ||
| + | |||
| + | '''Замечание.''' В предыдущем примере было бы точнее ответ записать так: [[Изображение:37.png]] (3) | ||
| + | |||
| + | Однако запись (2) более компактна и с ней удобнее проводить дальнейшие вычисления, если таковые потребуются. Поэтому запись ответа в виде (2) предпочтительнее, если элементы матриц - целые числа. И наоборот, если элементы матрицы - десятичные дроби, то обратную матрицу лучше записать без множителя <tex> \frac{1}{|A|} </tex> впереди. | ||
| + | |||
| + | '''Замечание.''' При нахождении обратной матрицы приходится выполнять довольно много вычислений и необычно правило расстановки алгебраических дополнений в итоговой матрице. Поэтому велика вероятность ошибки. Чтобы избежать ошибок следует делать проверку: вычислить произведение исходной матрицы на итоговую в том или ином порядке. Если в результате получится единичная матрица, то обратная матрица найдена правильно. В противном случае нужно искать ошибку. | ||
| + | |||
| + | '''Пример.''' Найдите обратную матрицу для матрицы [[Изображение:38.png]]. | ||
| + | |||
| + | '''Решение.''' | ||
| + | [[Изображение:39.png]] - существует. | ||
| + | |||
| + | [[Изображение:40.png]] | ||
| + | |||
| + | [[Изображение:41.png]] | ||
| + | |||
| + | '''Ответ:''' [[Изображение:42.png]]. | ||
| + | |||
| + | '''Вывод.''' Нахождение обратной матрицы по формуле (1) требует слишком много вычислений. Для матриц четвертого порядка и выше это неприемлемо. Реальный алгоритм нахождения обратной матрицы будет приведен позже. | ||
=== Вычисление определителя и обратной матрицы с помощью метода Гаусса === | === Вычисление определителя и обратной матрицы с помощью метода Гаусса === | ||
| - | == | + | Метод Гаусса можно использовать для нахождения определителя и обратной матрицы [5, стр.316-317]. |
| - | == | + | |
| - | == | + | Именно, определитель матрицы <tex> A </tex> равен det <tex>(A) = a_{11}a^{(1)}_{22} ... a^{(n-1)}_{nn} </tex>. |
| - | === | + | |
| - | = | + | Обратная матрица <tex> A^{-1} </tex> находится решением <tex> n </tex> систем линейных уравнений методом исключения Гаусса: |
| - | == | + | |
| - | = | + | <tex> Ax[j] = e[j] </tex>, где <tex> e[j] </tex> есть j-тый столбец единичной матрицы <tex> E </tex>, <tex> x[j] </tex> - искомый вектор. |
| + | |||
| + | Полученные векторы решений <tex> x[1], x[2], ..., x[n] </tex> - образуют, очевидно, <tex> n </tex> столбцов матрицы <tex> A^{-1} </tex>, поскольку <tex> AA^{-1} = E </tex>. | ||
| + | |||
| + | == Формулы для определителя == | ||
| + | |||
| + | '''1.''' Если матрица <tex> A </tex> невырожденная, то <tex> A = P^{-1}LDU </tex> и | ||
| + | <tex> \det A = \det P^{-1} \det L \det D \det U = \pm </tex>(произведение ведущих элементов). | ||
| + | |||
| + | Знак плюс или минус дается определителем матрицы <tex> P^{-1} </tex> (или <tex> P </tex>) и зависит от того, является число перестановок строк в приведении четным или нечетным. Для треугольных сомножителей имеем <tex> \det L = \det U = 1 </tex> и <tex> \det D = d_1 ... d_n </tex> | ||
| + | |||
| + | '''2.''' Определитель матрицы <tex> A </tex> может быть вычислен разлоразложением по алгебраическим дополнениям i-й строки: | ||
| + | |||
| + | <tex> \det A = a_{i1}A_{i1} + a_{i2}A_{i2} + ... + a_{in}A_{in} </tex>. | ||
| + | |||
| + | '''Алгебраическое дополнение''' <tex> \det A_{ij} </tex> есть определитель подподматрицы | ||
| + | <tex> M_{ij} </tex>, взятый с нужным знаком: | ||
| + | |||
| + | <tex> A_{ij} = (-1)^{i+j} \det M_{ij} </tex>. | ||
| + | |||
| + | Подматрица <tex> M_{ij} </tex> образуется вычеркиванием i-й строки и j-го столбца матрицы <tex> A </tex>. | ||
| + | |||
| + | '''3.''' '''Правило Крамера:''' j-й элемент вектора <tex> x = A^{-1} b </tex> равен | ||
| + | <tex> x_j = \frac {\det B_j}{\det A} </tex>, где | ||
| + | |||
| + | ::[[Изображение:S1.png]] | ||
| + | |||
| + | В <tex> B_j </tex> - вектор <tex> b </tex> заменяет собой j-й столбец матрицы <tex> A </tex>. | ||
| + | |||
| + | '''Пример.''' | ||
| + | |||
| + | Решение системы | ||
| + | |||
| + | ::[[Изображение:S2.png]] | ||
| + | |||
| + | '''4.''' '''Формула для ведущих элементов.''' | ||
| + | |||
| + | Если матрица <tex> A </tex> представляется в виде <tex> LDU </tex>, то левые верхние углы удовлетворяют соотношению | ||
| + | |||
| + | <tex> A_k = L_k D_k U_k </tex> | ||
| + | |||
| + | Для разных <tex> k </tex> разложения подматриц <tex> A_k </tex> «согласованы» друг с другом. | ||
| + | |||
| + | == Объем параллелепипеда == | ||
| + | |||
| + | Связь между определителем и объемом не очевидна, однако мы можем предположить для начала, что все углы прямые, т. е. грани взаимно перпендикулярны, и мы имеем дело с прямоугольным параллелепипедом. Тогда объем его равен просто произведению длин ребер <tex> l_1 l_2 ... l_n </tex>. | ||
| + | |||
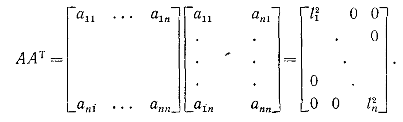
| + | Мы хотим получить ту же самую формулу с помощью определителя. С этой целью вспомним, что ребра параллелепипеда представляются строками матрицы <tex> A </tex>. В нашем случае эти строки | ||
| + | взаимно ортогональны, так что | ||
| + | |||
| + | ::[[Изображение:S3.png]] | ||
| + | |||
| + | Величины <tex> l^{2}_{i} </tex> суть квадраты длин строк матрицы, т. е. квадраты длин ребер, и нули вне диагонали получаются вследствие ортогональности строк. Переходя к определителям, получаем | ||
| + | |||
| + | ::[[Изображение:S4.png]] | ||
| + | |||
| + | Извлекая корень, мы и приходим к требуемому соотношению: | ||
| + | ''определитель равняется объему''. Знак при <tex> \det A </tex> будет зависеть от того, образуют ребра правостороннюю систему координат вида <tex> xyz </tex> или левостороннюю <tex> xyz </tex>. | ||
| + | |||
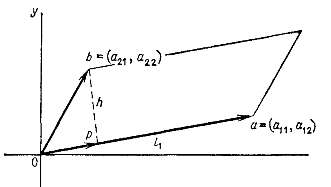
| + | Если область не прямоугольна, то объем уже не равен произведению длин ребер. В плоском случае «объем» параллелограмма равен произведению длины основания на высоту <tex> h </tex>. | ||
| + | |||
| + | Вектор <tex> pb </tex> длины <tex> h </tex> есть разность между вектором второй строки <tex> Ob = (a_{21}, a_{22}) </tex> и его проекцией <tex> Op </tex> на вектор первой строки. | ||
| + | |||
| + | ::[[Изображение:S5.png]] | ||
| + | |||
| + | Площадь паралелограмма равна <tex> \det A </tex>. | ||
| + | |||
| + | ::[[Изображение:S6.png]] | ||
| + | |||
| + | Площади квадрата и параллелограмма. | ||
| + | |||
| + | Первый представляет собой единичный квадрат, и его площадь, равна 1. Второй есть параллелограмм с единичными основанием и высотой; его площадь не зависит от «сдвига», даваемого коэффициентом <tex> c </tex>, и равна 1. | ||
| + | |||
== Литература == | == Литература == | ||
# http://e-lib.gasu.ru/eposobia/metody/ | # http://e-lib.gasu.ru/eposobia/metody/ | ||
# http://www.exponenta.ru/educat/systemat/slivina/lection/lection2/lection2.asp | # http://www.exponenta.ru/educat/systemat/slivina/lection/lection2/lection2.asp | ||
# http://elib.ispu.ru/library/math/sem1/index.html | # http://elib.ispu.ru/library/math/sem1/index.html | ||
| + | # [[Вычисление матриц Якоби и Гессе]] | ||
# Киселёв В.Ю., Пяртли А.С., Калугина Т.Ф. Высшая математика. | # Киселёв В.Ю., Пяртли А.С., Калугина Т.Ф. Высшая математика. | ||
| - | # Боглаев Ю.П. Вычислительная математика и программирование. - М., Высшая школа, 1990, | + | # Боглаев Ю.П. Вычислительная математика и программирование. - М., Высшая школа, 1990, 544 с. |
| - | + | # Стренг Г. Линейная алгебра и ее приминения / Под ред. Г. И. Марчука. М.: Мир, 1980. 453 c. | |
== См. также == | == См. также == | ||
| Строка 152: | Строка 276: | ||
{{stub}} | {{stub}} | ||
| - | [[Категория: | + | [[Категория:Линейная алгебра]] |
[[Категория:Учебные задачи]] | [[Категория:Учебные задачи]] | ||
Текущая версия
Содержание |
Постановка задачи
Задание подразумевает знакомство пользователя с основными понятиями численных методов, такими как определитель и обратная матрица, и различными способами их вычислений. В данном теоретическом отчете простым и доступным языком сначала вводятся основные понятия и определения, на основании которых проводится дальнейшее исследование. Пользователь может не иметь специальных знаний в области численных методов и линейной алгебры, но с легкостью сможет воспользоваться результатами данной работы. Для наглядности приведена программа вычисления определителя матрицы несколькими методами, написанная на языке программирования C++. Программа используется как лабораторный стенд для создания иллюстраций к отчету. А также проводится исследование методов для решения систем линейных алгебраических уравнений. Доказывается бесполезность вычисления обратной матрицы, поэтому в работе приводится более оптимальные способы решения уравнений не вычисляя ее. Рассказывается почему существует такое количество различных методов вычисления определителей и обратных матриц и разбираются их недостатки. Также рассматриваются погрешности при вычислении определителя и оценивается достигнутая точность. Помимо русских терминов в работе используются и их английские эквиваленты для понимания, под какими названиями искать численные процедуры в библиотеках и что означают их параметры.
Основные определения и простейшие свойства
Определитель
Введем определение определителя квадратной матрицы любого порядка. Это определение будет рекуррентным, то есть чтобы установить, что такое определитель матрицы порядка , нужно уже знать, что такое определитель матрицы порядка
. Отметим также, что определитель существует только у квадратных матриц.
Определитель квадратной матрицы будем обозначать
или det
.
Определение 1. Определителем квадратной матрицы 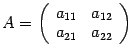 второго порядка называется число
второго порядка называется число ![]() .
.
Определителем 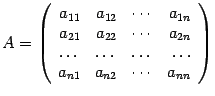 квадратной матрицы порядка
квадратной матрицы порядка ,
, называется число
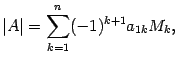
где - определитель матрицы порядка
, полученной из матрицы
вычеркиванием первой строки и столбца с номером
.
Для наглядности запишем, как можно вычислить определитель матрицы четвертого порядка: 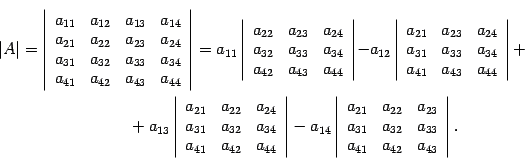
Замечание. Реальное вычисление определителей для матриц выше третьего порядка на основе определения используется в исключительных случаях. Как правило, вычисление ведется по другим алгоритмам, которые будут рассмотрены позже и которые требуют меньше вычислительной работы.
Замечание. В определении 1 было бы точнее сказать, что определитель есть функция, определенная на множестве квадратных матриц порядка и принимающая значения в множестве чисел.
Замечание. В литературе вместо термина "определитель" используется также термин "детерминант", имеющий тот же самый смысл. От слова "детерминант" и появилось обозначение det .
Рассмотрим некоторые свойства определителей, которые сформулируем в виде утверждений.
Утверждение 1. При транспонировании матрицы определитель не меняется, то есть .
Утверждение 2. Определитель произведения квадратных матриц равен произведению определителей сомножителей, то есть .
Утверждение 3. Если в матрице поменять местами две строки, то ее определитель сменит знак.
Утверждение 4. Если матрица имеет две одинаковые строки, то ее определитель равен нулю.
В дальнейшем нам потребуется складывать строки и умножать строку на число. Эти действия над строками (столбцами) мы будем выполнять так же, как действия над матрицами-строками (матрицами-столбцами), то есть поэлементно. Результатом будет служить строка (столбец), как правило, не совпадающая со строками исходной матрицы. При наличии операций сложения строк (столбцов) и умножения их на число мы можем говорить и о линейных комбинациях строк (столбцов), то есть суммах с числовыми коэффициентами.
Утверждение 5. Если строку матрицы умножить на число , то ее определитель умножится на это число.
Утверждение 6. Если матрица содержит нулевую строку, то ее определитель равен нулю.
Утверждение 7. Если одна из строк матрицы равна другой, умноженной на число (строки пропорциональны), то определитель матрицы равен нулю.
Утверждение 8. Пусть в матрице i-ая строка имеет вид
. Тогда
, где матрица
получается из матрицы
заменой i-ой строки на строку
, а матрица
- заменой i-ой строки на строку
.
Утверждение 9. Если к одной из строк матрицы добавить другую, умноженную на число, то определитель матрицы не изменится.
Утверждение 10. Если одна из строк матрицы является линейной комбинацией других ее строк, то определитель матрицы равен нулю.
Определение 2. Алгебраическим дополнением к элементу матрицы
называется число, равное
, где
- определитель матрицы, полученной из матрицы вычеркиванием i-ой строки и j-ого столбца.
Алгебраическое дополнение к элементу
матрицы
обозначается
.
Замечание. Используя алгебраические дополнения, определение 1 определителя можно записать так: 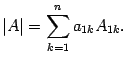
Утверждение 11. Разложение определителя по произвольной строке.
Для определителя матрицы справедлива формула
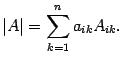
Решение. Воспользуемся разложением по третьей строке, так выгоднее, поскольку в третьей строке два числа из трех - нули. Получим 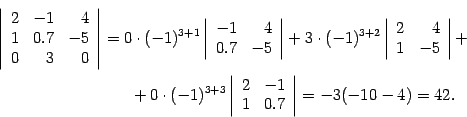
Утверждение 12. Для квадратной матрицы порядка
при
выполнено соотношение
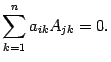 .
.
Утверждение 13. Все свойства определителя, сформулированные для строк (утверждения 1 - 11), справедливы и для столбцов, в частности, справедливо разложение определителя по j-ому столбцу 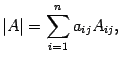 и равенство
и равенство 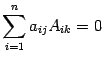 при
при .
Утверждение 14. Определитель треугольной матрицы равен произведению элементов ее главной диагонали.
Следствие. Определитель единичной матрицы равен единице, .
Вывод. Перечисленные выше свойства позволяют находить определители матриц достаточно высоких порядков при сравнительно небольшом объеме вычислений. Алгоритм вычислений следующий.
Алгоритм создания нулей в столбце.
Пусть требуется вычислить определитель порядка
. Если
, то поменяем местами первую строку и любую другую, в которой первый элемент не нуль. В результате определитель
, будет равен определителю новой матрицы с противоположным знаком. Если же первый элемент каждой строки равен нулю, то матрица
имеет нулевой столбец и по утверждениям 1, 13 ее определитель равен нулю.
Итак, считаем, что уже в исходной матрице . Первую строку оставляем без изменений. Прибавим ко второй строке первую строку, умноженную на число
. Тогда первый элемент второй строки будет равен
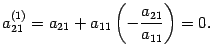 .
.
Остальные элементы новой второй строки обозначим ,
. Определитель новой матрицы по утверждению 9 равен
.
Первую строку умножим на число
и прибавим к третьей. Первый элемент новой третьей строки будет равен
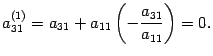
Остальные элементы новой третьей строки обозначим ,
. Определитель новой матрицы по утверждению 9 равен
.
Процесс получения нулей вместо первых элементов строк продолжим дальше. Наконец, первую строку умножим на число и прибавим к последней строке. В результате получается матрица, обозначим ее
, которая имеет вид
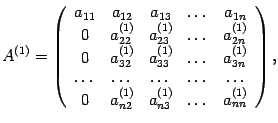
причем . Для вычисления определителя матрицы
используем разложение по первому столбцу
![]()
В правой части стоит определитель матрицы порядка . К нему применим тот же алгоритм, и вычисление определителя матрицы сведется к вычислению определителя матрицы порядка
. Процесс повторяем до тех пор, пока не дойдем до определителя второго порядка, который вычисляется по определению.
Если матрица не обладает какими-то специфическими свойствами, то заметно уменьшить объем вычислений по сравнению с предложенным алгоритмом не удается. Еще одна хорошая сторона этого алгоритма - по нему легко составить программу для компьютера для вычисления определителей матриц больших порядков. В стандартных программах вычисления определителей используется этот алгоритм с не принципиальными изменениями, связанными с минимизацией влияния ошибок округления и погрешностей входных данных при вычислениях компьютера.
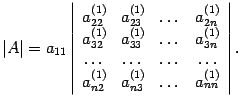
Пример. Вычислите определитель матрицы 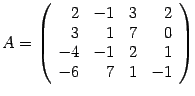 .
.
Решение. Первую строку оставляем без изменения. Ко второй строке прибавляем первую, умноженную на число :
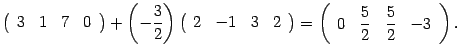
Определитель не меняется. К третьей строке прибавляем первую, умноженную на число :
![]()
Определитель не меняется. К четвертой строке прибавляем первую, умноженную на число :
![]()
Определитель не меняется. В результате получаем 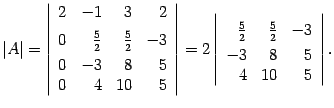
По тому же алгоритму считаем определитель матрицы порядка 3, стоящий справа. Первую строку оставляем без изменений, ко второй строке прибавляем первую, умноженную на число 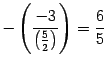 :
:
К третьей строке прибавляем первую, умноженную на число 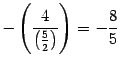 :
:
Ответ. .
Замечание. Хотя при вычислениях использовались дроби, результат оказался целым числом. Действительно, используя свойства определителей и то, что исходные числа - целые, операций с дробями можно было бы избежать. Но в инженерной практике числа крайне редко бывают целыми. Поэтому, как правило, элементы определителя будут десятичными дробями и применять какие-то ухищрения для упрощения вычислений нецелесообразно.
Обратная матрица
Определение 3. Матрица называется обратной матрицей для квадратной матрицы
, если
.
Из определения следует, что обратная матрица будет квадратной матрицей того же порядка, что и матрица
(иначе одно из произведений
или
было бы не определено).
Обратная матрица для матрицы обозначается
. Таким образом, если
существует, то
.
Из определения обратной матрицы следует, что матрица является обратной для матрицы
, то есть
. Про матрицы
и
можно говорить, что они обратны друг другу или взаимно обратны.
Если определитель матрицы равен нулю, то обратная к ней не существует.
Так как для нахождения обратной матрицы важно, равен ли определитель марицы нулю или нет, то введем следующие определения.
Определение 4. Квадратную матрицу назовем вырожденной или особенной матрицей, если
, и невырожденной или неособенной матрицей, если
.
Утверждение. Если обратная матрица существует, то она единственна.
Утверждение. Если квадратная матрица является невырожденной, то обратная для нее существует и
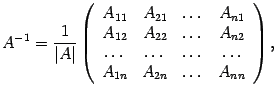 (1)
где
(1)
где - алгебраические дополнения к элементам
.
Теорема.
Обратная матрица для квадратной матрицы существует тогда и только тогда, когда матрица
- невырожденная, обратная матрица единственна, и справедлива формула (1).
Замечание. Следует обратить особое внимание на места, занимаемые алгебраическими дополнениями в формуле обратной матрицы: первый индекс показывает номер столбца, а второй - номер строки, в которые нужно записать вычисленное алгебраическое дополнение.
Пример. Найдите обратную матрицу для матрицы 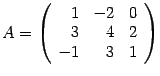 .
.
Так как , то матрица
- невырожденная, и обратная для нее существует.
Находим алгебраические дополнения:
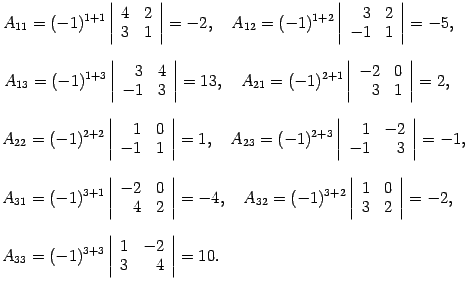
Составляем обратную матрицу, размещая найденные алгебраические дополнения так, чтобы первый индекс соответствовал столбцу, а второй - строке: 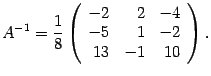 (2)
(2)
Полученная матрица (2) и служит ответом к задаче.
Замечание. В предыдущем примере было бы точнее ответ записать так: 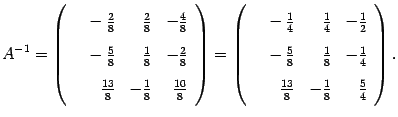 (3)
(3)
Однако запись (2) более компактна и с ней удобнее проводить дальнейшие вычисления, если таковые потребуются. Поэтому запись ответа в виде (2) предпочтительнее, если элементы матриц - целые числа. И наоборот, если элементы матрицы - десятичные дроби, то обратную матрицу лучше записать без множителя впереди.
Замечание. При нахождении обратной матрицы приходится выполнять довольно много вычислений и необычно правило расстановки алгебраических дополнений в итоговой матрице. Поэтому велика вероятность ошибки. Чтобы избежать ошибок следует делать проверку: вычислить произведение исходной матрицы на итоговую в том или ином порядке. Если в результате получится единичная матрица, то обратная матрица найдена правильно. В противном случае нужно искать ошибку.
Пример. Найдите обратную матрицу для матрицы 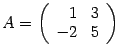 .
.
Вывод. Нахождение обратной матрицы по формуле (1) требует слишком много вычислений. Для матриц четвертого порядка и выше это неприемлемо. Реальный алгоритм нахождения обратной матрицы будет приведен позже.
Вычисление определителя и обратной матрицы с помощью метода Гаусса
Метод Гаусса можно использовать для нахождения определителя и обратной матрицы [5, стр.316-317].
Именно, определитель матрицы равен det
.
Обратная матрица находится решением
систем линейных уравнений методом исключения Гаусса:
, где
есть j-тый столбец единичной матрицы
,
- искомый вектор.
Полученные векторы решений - образуют, очевидно,
столбцов матрицы
, поскольку
.
Формулы для определителя
1. Если матрица невырожденная, то
и
(произведение ведущих элементов).
Знак плюс или минус дается определителем матрицы (или
) и зависит от того, является число перестановок строк в приведении четным или нечетным. Для треугольных сомножителей имеем
и
2. Определитель матрицы может быть вычислен разлоразложением по алгебраическим дополнениям i-й строки:
.
Алгебраическое дополнение есть определитель подподматрицы
, взятый с нужным знаком:
.
Подматрица образуется вычеркиванием i-й строки и j-го столбца матрицы
.
3. Правило Крамера: j-й элемент вектора равен
, где
В - вектор
заменяет собой j-й столбец матрицы
.
Пример.
Решение системы
4. Формула для ведущих элементов.
Если матрица представляется в виде
, то левые верхние углы удовлетворяют соотношению
Для разных разложения подматриц
«согласованы» друг с другом.
Объем параллелепипеда
Связь между определителем и объемом не очевидна, однако мы можем предположить для начала, что все углы прямые, т. е. грани взаимно перпендикулярны, и мы имеем дело с прямоугольным параллелепипедом. Тогда объем его равен просто произведению длин ребер .
Мы хотим получить ту же самую формулу с помощью определителя. С этой целью вспомним, что ребра параллелепипеда представляются строками матрицы . В нашем случае эти строки
взаимно ортогональны, так что
Величины суть квадраты длин строк матрицы, т. е. квадраты длин ребер, и нули вне диагонали получаются вследствие ортогональности строк. Переходя к определителям, получаем
Извлекая корень, мы и приходим к требуемому соотношению:
определитель равняется объему. Знак при будет зависеть от того, образуют ребра правостороннюю систему координат вида
или левостороннюю
.
Если область не прямоугольна, то объем уже не равен произведению длин ребер. В плоском случае «объем» параллелограмма равен произведению длины основания на высоту .
Вектор длины
есть разность между вектором второй строки
и его проекцией
на вектор первой строки.
Площадь паралелограмма равна .
Площади квадрата и параллелограмма.
Первый представляет собой единичный квадрат, и его площадь, равна 1. Второй есть параллелограмм с единичными основанием и высотой; его площадь не зависит от «сдвига», даваемого коэффициентом , и равна 1.
Литература
- http://e-lib.gasu.ru/eposobia/metody/
- http://www.exponenta.ru/educat/systemat/slivina/lection/lection2/lection2.asp
- http://elib.ispu.ru/library/math/sem1/index.html
- Вычисление матриц Якоби и Гессе
- Киселёв В.Ю., Пяртли А.С., Калугина Т.Ф. Высшая математика.
- Боглаев Ю.П. Вычислительная математика и программирование. - М., Высшая школа, 1990, 544 с.
- Стренг Г. Линейная алгебра и ее приминения / Под ред. Г. И. Марчука. М.: Мир, 1980. 453 c.