Статистический отчет при создании моделей

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(→Описание решения)
 
(41 промежуточная версия не показана)
Строка 14: Строка 14:
Будем считать,
Будем считать,
-
что зависимость
+
что зависимость имеет вид
<tex>y(x) = f(x) + \varepsilon(x)</tex>,
<tex>y(x) = f(x) + \varepsilon(x)</tex>,
Строка 21: Строка 21:
<tex>\varepsilon(x)</tex> &nbsp;&#151; случайная величина,
<tex>\varepsilon(x)</tex> &nbsp;&#151; случайная величина,
с нулевым [[Математическое ожидание|математически ожиданием]].
с нулевым [[Математическое ожидание|математически ожиданием]].
-
В моделях [[Многомерная линейная регрессия|многомерной линейной регрессии]] предполагается, что неслучайная составляющая имеет вид:
+
В моделях предполагается, что неслучайная составляющая имеет вид:
-
<tex> f(x) = <w, \ x> </tex>.
+
* <tex> f(x) = <w, \ x> </tex> &nbsp;&#151; в [[Многомерная линейная регрессия|многомерной линейной регрессии]];
 +
 
 +
* <tex> f(x) = \sigma(<w, \ x>), \; \sigma(z) = \frac{1}{1 + \exp(-z)} </tex> и <tex>\mathbb{Y} = [0,1]</tex> &nbsp;&#151; в [[Логистическая регрессия|логистической регрессии]].
Требуется численно оценить качество модели при заданном векторе параметров <tex> w</tex>.
Требуется численно оценить качество модели при заданном векторе параметров <tex> w</tex>.
Строка 29: Строка 31:
== Описание решения ==
== Описание решения ==
-
В качестве оценки для <tex>w</tex> в статье будем использовать решение
+
Предполагая,
-
[[Метод наименьших квадратов| методом наименьших квадратов]]:
+
что матрица ковариации вектора ошибки <tex>\varepsilon = \(\varepsilon_1 <br> \ \vdots\ <br> \varepsilon_l\) </tex> имеет вид
 +
<tex>\sigma^2 V </tex>,
 +
где <tex> V = diag (v_1, \dots, v_l) </tex>
 +
(<tex>V</tex> может быть задана пользователем, иначе выбирается единичная матрица),
 +
получаем выражение для оценки параметров <tex>w</tex>
 +
[[Метод наименьших квадратов| взвешенным методом наименьших квадратов]]:
-
<tex> \hat w = (X^T X)^{-1} X^T y. </tex>
+
<tex> \hat w = (X^T V^{-1} X)^{-1} X^T V^{-1} y. </tex>
Основными инструментами оценки качества линейной модели является анализ:
Основными инструментами оценки качества линейной модели является анализ:
Строка 40: Строка 47:
* корреляции и ковариации коэффициентов регрессии;
* корреляции и ковариации коэффициентов регрессии;
* [[Статистика Дарбина-Уотсона|статистики Дарбина-Уотсона]];
* [[Статистика Дарбина-Уотсона|статистики Дарбина-Уотсона]];
-
* расстояния Махаланобиса между исходной зависимостью и модельной;
+
* расстояния Махаланобиса между исходной и модельной зависимостями;
* расстояния Кука (мера изменения прогноза при удалении одного объекта);
* расстояния Кука (мера изменения прогноза при удалении одного объекта);
* [[Доверительный интервал|доверительных интервалов]] для предсказанных значений.
* [[Доверительный интервал|доверительных интервалов]] для предсказанных значений.
 +
 +
Для оценки качества модели линейной регрессии в работе рассматривается
 +
 +
* анализ регрессионных остатков, включающий в себя:
 +
** вычисление среднеквадратичной ошибки:
 +
<tex>\mathbb{MSE} = \sum_{i=1}^l \left(y_i - f\left(x_i\right)\right)^2;</tex>
 +
** вычисление коэффициента детерминации:
 +
<tex>\mathbb{R}^2 = 1 - \frac{\sum_{i=1}^l \left(y_i - f\left(x_i\right)\right)^2}{\sum_{i=1}^l \left(y_i - \bar y\right)^2}, </tex>
 +
где <tex>\bar y = \frac{1}{l} \sum_{i=1}^l y_i;</tex>
 +
** проверку гипотезы о равенстве нулю математического ожидания регрессионных остатков на основе [[Критерий знаков|критерия знаков]];
 +
** проверку гипотезы о равенстве дисперсий (пропорциональности с заданными коэффициентами) регрессионных остатков на основе критерия [http://www.mathworks.com/help/toolbox/stats/ansaribradley.html Ансари-Брэдли];
 +
** проверку гипотезы о нормальности распределения регрессионных остатков на основе критерия хи-квадрат и критерия [http://en.wikipedia.org/wiki/Jarque%E2%80%93Bera_test Жарка-Бера];
 +
* вычисление расстояния [http://ru.wikipedia.org/wiki/%D0%A0%D0%B0%D1%81%D1%81%D1%82%D0%BE%D1%8F%D0%BD%D0%B8%D0%B5_%D0%9C%D0%B0%D1%85%D0%B0%D0%BB%D0%B0%D0%BD%D0%BE%D0%B1%D0%B8%D1%81%D0%B0 Махаланобиса] и [http://en.wikipedia.org/wiki/Cook's_distance Кука];
 +
* вычисление корреляций признаков, корреляций признаков и значений моделируемой функции и коэффициента множественной регрессии.
 +
 +
Для оценки качества модели логистической регрессии в работе рассматриваются оценки
 +
 +
* дисперсии шума модели;
 +
* корреляции и ковариации коэффициентов регрессии;
 +
* значимости компонент пространства объектов для восстановления ответов;
== Вычислительный эксперимент ==
== Вычислительный эксперимент ==
 +
 +
В данном отчете представлены результаты применения созданного инструмента для анализа модели.
 +
Отчет состоит из пяти экспериментов, демонстрирующих работу инструмента на различных по качеству моделях.
 +
Модели 1-3 приведены для линейной регрессии, 4-5 &nbsp;&#151; для логистической.
 +
 +
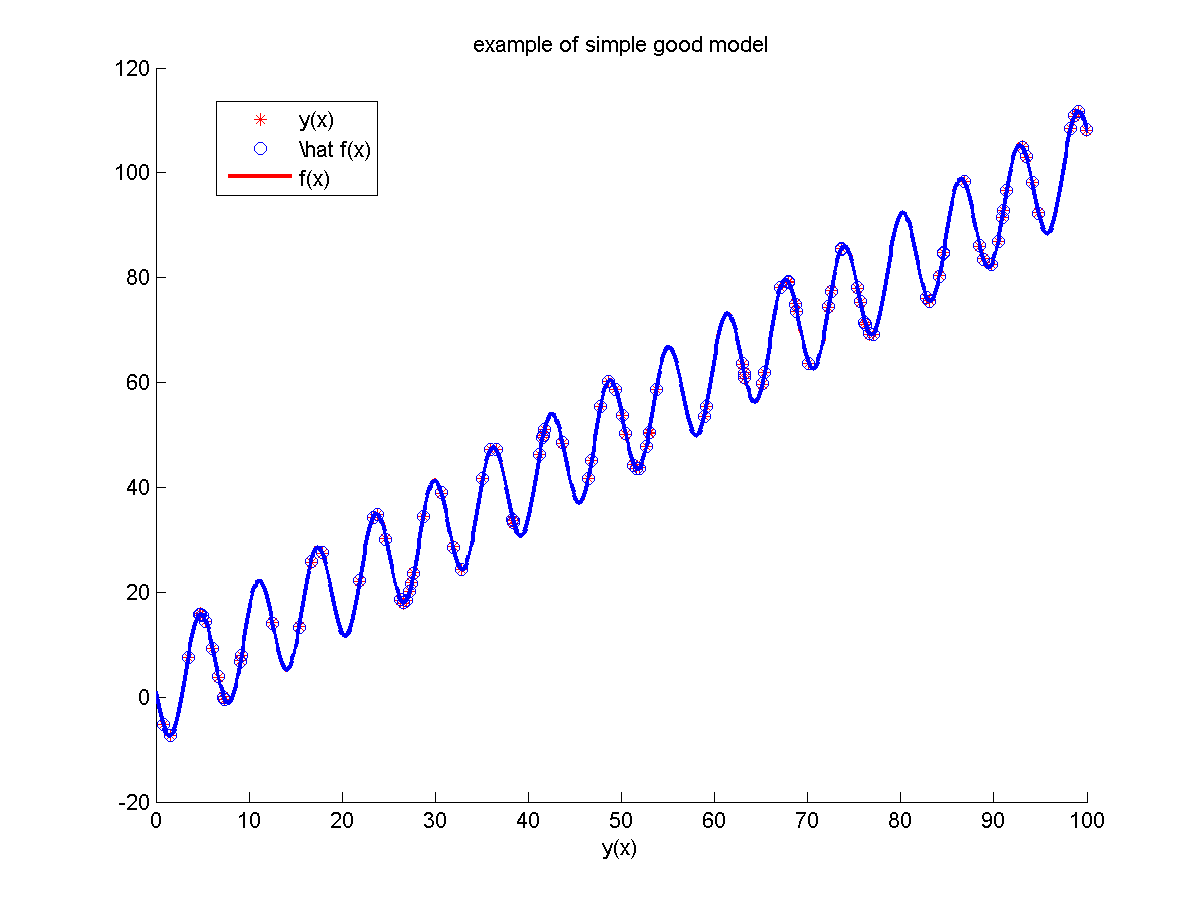
=== Модель №1 ===
 +
 +
Неизвестная зависимость:
 +
<tex> y(x) = x - 10 \sin(x) + \exp(x / 100)</tex>.
 +
 +
Для построения модели использовалось <tex>100</tex> объектов независимо равномерно распределительных на отрезке <tex>[0, 100].</tex>
 +
В качестве шума использовались независимые случайные величины из распределения <tex>N(0, \; 0,1).</tex>
 +
В качестве признаков использовались <tex>x, \; \sin(x), \;\exp(x / 100)</tex>.
 +
Параметры модели подбирались с помощью метода наименьших квадратов.
 +
 +
[[image:statModelAnalisys01.png]]
 +
 +
Отчет, построенный программой:
 +
 +
[https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Yanovich2011StatModel/simpleExampleGoodModel.txt отчет №1.]
 +
 +
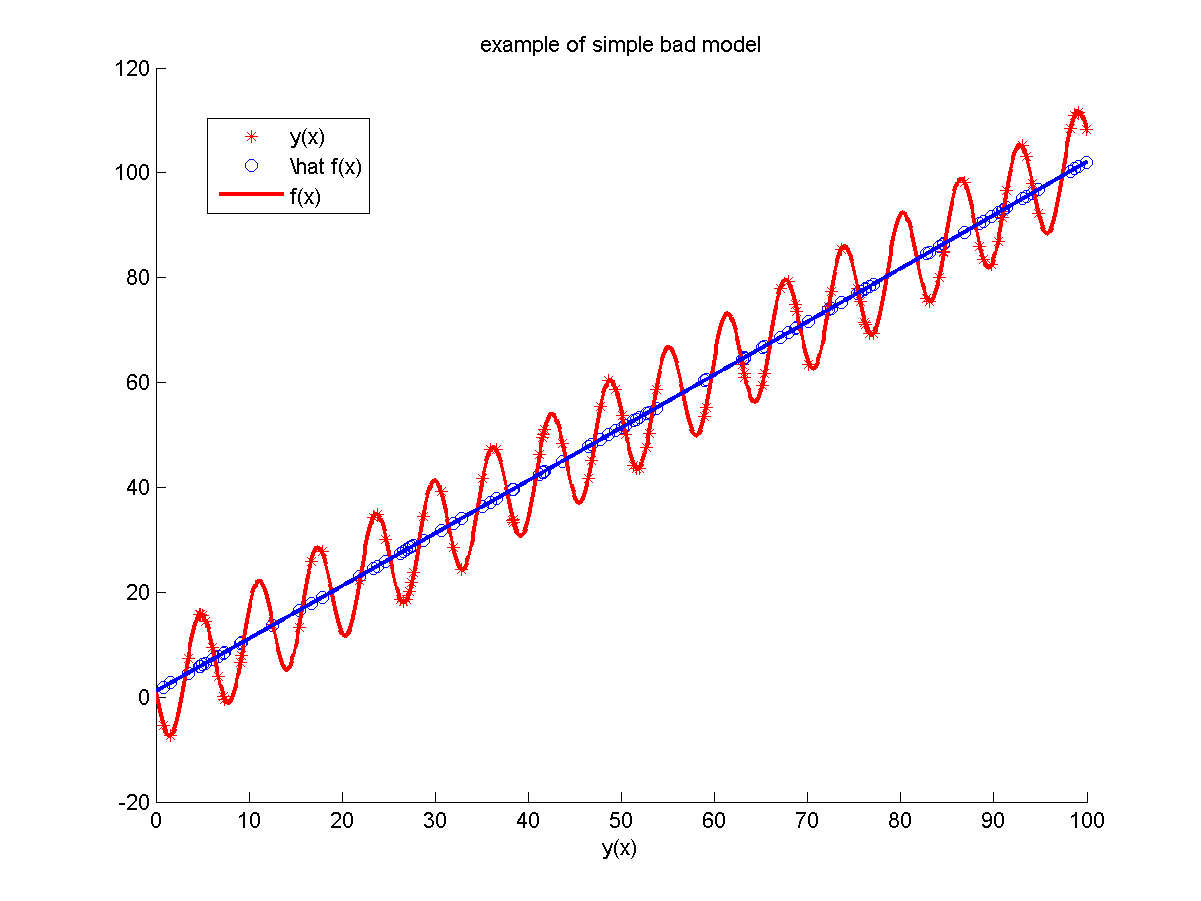
=== Модель №2 ===
 +
 +
Неизвестная зависимость:
 +
<tex> y(x) = x - 10 \sin(x) + \exp(x / 100)</tex>.
 +
 +
Для построения модели использовалось <tex>100</tex> объектов независимо равномерно распределительных на отрезке <tex>[0, 100].</tex>
 +
В качестве шума использовались независимые случайные величины из распределения <tex>N(0, \; 0,1).</tex>
 +
В качестве признаков использовались <tex>x, \;\exp(x / 100)</tex>.
 +
Параметры модели подбирались с помощью метода наименьших квадратов.
 +
 +
[[image:statModelAnalisys02.png]]
 +
 +
Отчет, построенный программой:
 +
 +
[https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Yanovich2011StatModel/simpleExampleBadModel.txt отчет №2.]
 +
 +
=== Модель №3 ===
 +
 +
Неизвестная зависимость:
 +
<tex> y(x) = x - 10 \sin(x) + \exp(x / 100)</tex>.
 +
 +
Для построения модели использовалось <tex>100</tex> объектов независимо равномерно распределительных на отрезке <tex>[0, 100].</tex>
 +
В качестве шума использовались независимые случайные величины из распределения <tex>N(0, \; x).</tex>
 +
В качестве признаков использовались <tex> y(x) = x - 10 \sin(x) + \exp(x / 100)</tex>.
 +
Параметры модели подбирались с помощью метода наименьших квадратов.
 +
 +
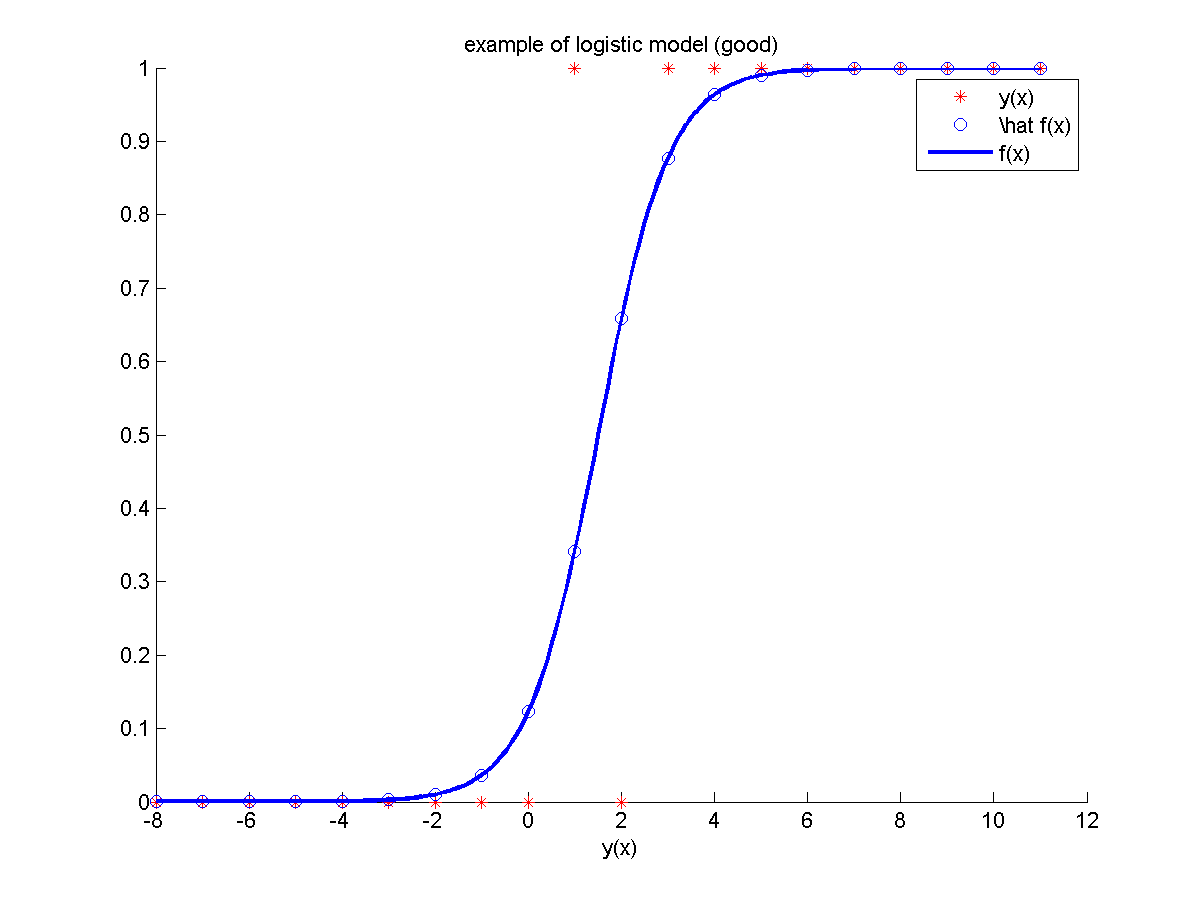
=== Модель №4 ===
 +
 +
Неизвестная зависимость:
 +
<tex> y(x) = I(x > 0), </tex>.
 +
где <tex> I(A) </tex> &nbsp;&#151; индикаторная функция множества <tex> A </tex>.
 +
 +
Для построения модели использовалось <tex>20</tex> объектов из равномерной сетки.
 +
Значение в одной из обучающих точек сильно зашумлено.
 +
В качестве признаков использовались константа, <tex> x </tex>.
 +
 +
[[image:statModelAnalisys04.png]]
 +
 +
Отчет, построенный программой:
 +
 +
[https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Yanovich2011StatModel/logisticGoodModel.txt отчет №4.]
 +
 +
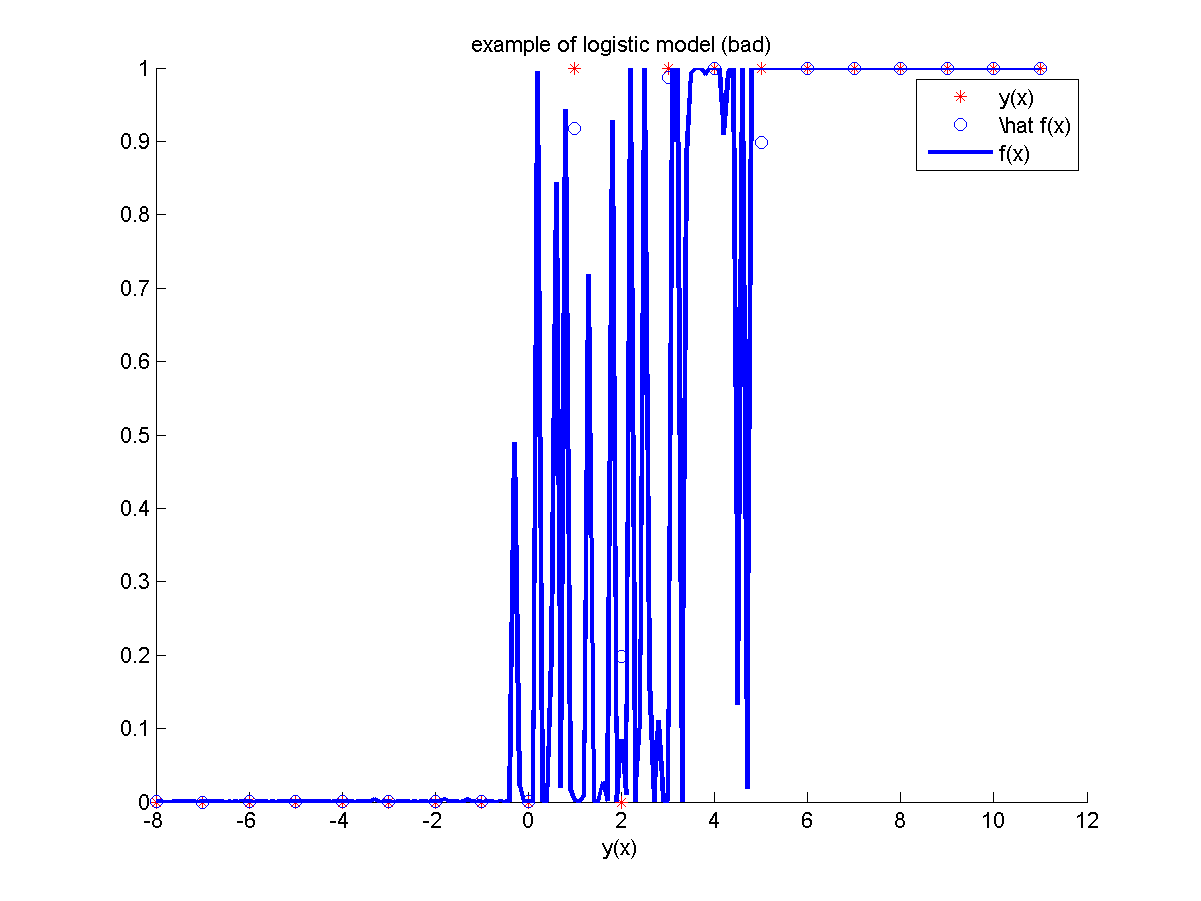
=== Модель №5 ===
 +
 +
Неизвестная зависимость:
 +
<tex> y(x) = I(x > 0), </tex>.
 +
где <tex> I(A) </tex> &nbsp;&#151; индикаторная функция множества <tex> A </tex>.
 +
 +
Для построения модели использовалось <tex>20</tex> объектов из равномерной сетки.
 +
Значение в одной из обучающих точек сильно зашумлено.
 +
В качестве признаков использовались константа, <tex> x </tex> и шумовой признак (порожден стандартным нормальным распределением).
 +
 +
[[image:statModelAnalisys05.png]]
 +
 +
Отчет, построенный программой:
 +
 +
[https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Yanovich2011StatModel/logisticBadModel.txt отчет №5.]
== Исходный код и полный текст работы ==
== Исходный код и полный текст работы ==
-
* [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Surname2011Title/ Surname2011Title]
+
 
 +
[https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Yanovich2011StatModel Функция, строящая отчет, и примеры.]
== Смотри также ==
== Смотри также ==
* [[Многомерная случайная величина]]
* [[Многомерная случайная величина]]
 +
* [[Анализ регрессионных остатков (пример)]]
== Литература ==
== Литература ==
-
* [http://ya.ru Bishop, C. Pattern Recognition And Machine Learning. Springer. 2006.]
+
# [http://ya.ru Bishop, C. Pattern Recognition And Machine Learning. Springer. 2006.]
-
{{Задание|Юрий Янович|В.В. Стрижов|28 мая 2009|Aurelius|Strijov}}
+
# ''Кобзарь А. И.'' Прикладная математическая статистика. — М.:&nbsp;Физматлит, 2006.
 +
# ''Лагутин М. Б.'' Наглядная математическая статистика. В двух томах. — М.: П-центр, 2003.
 +
# ''Hosmer W. D. , Lemeshow S.'' Applied logistic regression - New York: John Wiley & Sons, 2000.
 +
 
 +
{{ЗаданиеВыполнено|Юрий Янович|В.В. Стрижов|28 мая 2009|Aurelius|Strijov}}
[[Категория:Практика и вычислительные эксперименты]]
[[Категория:Практика и вычислительные эксперименты]]
[[Категория:Регрессионный анализ]]
[[Категория:Регрессионный анализ]]

Текущая версия

Содержание

В данной работе приведен обзор статистических методов оценивания качества регрессионных моделей, используемых популярными программами машинного обучения и статистической обработки данных. Приведены примеры вычисления и анализа полученных оценок.

Постановка задачи

Имеется пространство объектов-строк \mathbb{X} = \mathbb{R}^n и пространство ответов \mathbb{Y} = \mathbb{R}. Задана выборка (x_i,\ y_i)_{i=1}^l \in \mathbb{X} \times \mathbb{Y}. Обозначеним:

  • X = \(x_1 <br> \ \vdots\ <br> x_l\)  — матрица информации или матрица плана;
  • w = \(w_1<br> \ \vdots <br> w_n\)  — вектор параметров;
  • y = \(y_1<br>\ \vdots<br>y_l\)  — целевой вектор.

Будем считать, что зависимость имеет вид

y(x) = f(x) + \varepsilon(x),

где f(x)  — некоторая неслучайная функция, \varepsilon(x)  — случайная величина, с нулевым математически ожиданием. В моделях предполагается, что неслучайная составляющая имеет вид:

Требуется численно оценить качество модели при заданном векторе параметров w.

Описание решения

Предполагая, что матрица ковариации вектора ошибки \varepsilon = \(\varepsilon_1 <br> \ \vdots\ <br> \varepsilon_l\) имеет вид \sigma^2 V , где V = diag (v_1, \dots, v_l) (V может быть задана пользователем, иначе выбирается единичная матрица), получаем выражение для оценки параметров w взвешенным методом наименьших квадратов:

\hat w = (X^T V^{-1} X)^{-1} X^T V^{-1} y.

Основными инструментами оценки качества линейной модели является анализ:

Для оценки качества модели линейной регрессии в работе рассматривается

  • анализ регрессионных остатков, включающий в себя:
    • вычисление среднеквадратичной ошибки:

\mathbb{MSE} = \sum_{i=1}^l \left(y_i - f\left(x_i\right)\right)^2;

    • вычисление коэффициента детерминации:

\mathbb{R}^2 = 1 - \frac{\sum_{i=1}^l \left(y_i - f\left(x_i\right)\right)^2}{\sum_{i=1}^l \left(y_i - \bar y\right)^2}, где \bar y = \frac{1}{l} \sum_{i=1}^l y_i;

    • проверку гипотезы о равенстве нулю математического ожидания регрессионных остатков на основе критерия знаков;
    • проверку гипотезы о равенстве дисперсий (пропорциональности с заданными коэффициентами) регрессионных остатков на основе критерия Ансари-Брэдли;
    • проверку гипотезы о нормальности распределения регрессионных остатков на основе критерия хи-квадрат и критерия Жарка-Бера;
  • вычисление расстояния Махаланобиса и Кука;
  • вычисление корреляций признаков, корреляций признаков и значений моделируемой функции и коэффициента множественной регрессии.

Для оценки качества модели логистической регрессии в работе рассматриваются оценки

  • дисперсии шума модели;
  • корреляции и ковариации коэффициентов регрессии;
  • значимости компонент пространства объектов для восстановления ответов;

Вычислительный эксперимент

В данном отчете представлены результаты применения созданного инструмента для анализа модели. Отчет состоит из пяти экспериментов, демонстрирующих работу инструмента на различных по качеству моделях. Модели 1-3 приведены для линейной регрессии, 4-5  — для логистической.

Модель №1

Неизвестная зависимость: y(x) = x - 10 \sin(x) + \exp(x / 100).

Для построения модели использовалось 100 объектов независимо равномерно распределительных на отрезке [0, 100]. В качестве шума использовались независимые случайные величины из распределения N(0, \; 0,1). В качестве признаков использовались x, \; \sin(x), \;\exp(x / 100). Параметры модели подбирались с помощью метода наименьших квадратов.

image:statModelAnalisys01.png

Отчет, построенный программой:

отчет №1.

Модель №2

Неизвестная зависимость: y(x) = x - 10 \sin(x) + \exp(x / 100).

Для построения модели использовалось 100 объектов независимо равномерно распределительных на отрезке [0, 100]. В качестве шума использовались независимые случайные величины из распределения N(0, \; 0,1). В качестве признаков использовались x, \;\exp(x / 100). Параметры модели подбирались с помощью метода наименьших квадратов.

image:statModelAnalisys02.png

Отчет, построенный программой:

отчет №2.

Модель №3

Неизвестная зависимость: y(x) = x - 10 \sin(x) + \exp(x / 100).

Для построения модели использовалось 100 объектов независимо равномерно распределительных на отрезке [0, 100]. В качестве шума использовались независимые случайные величины из распределения N(0, \; x). В качестве признаков использовались y(x) = x - 10 \sin(x) + \exp(x / 100). Параметры модели подбирались с помощью метода наименьших квадратов.

Модель №4

Неизвестная зависимость: y(x) = I(x > 0), . где I(A)  — индикаторная функция множества A .

Для построения модели использовалось 20 объектов из равномерной сетки. Значение в одной из обучающих точек сильно зашумлено. В качестве признаков использовались константа, x .

image:statModelAnalisys04.png

Отчет, построенный программой:

отчет №4.

Модель №5

Неизвестная зависимость: y(x) = I(x > 0), . где I(A)  — индикаторная функция множества A .

Для построения модели использовалось 20 объектов из равномерной сетки. Значение в одной из обучающих точек сильно зашумлено. В качестве признаков использовались константа, x и шумовой признак (порожден стандартным нормальным распределением).

image:statModelAnalisys05.png

Отчет, построенный программой:

отчет №5.

Исходный код и полный текст работы

Функция, строящая отчет, и примеры.

Смотри также

Литература

  1. Bishop, C. Pattern Recognition And Machine Learning. Springer. 2006.
  2. Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006.
  3. Лагутин М. Б. Наглядная математическая статистика. В двух томах. — М.: П-центр, 2003.
  4. Hosmer W. D. , Lemeshow S. Applied logistic regression - New York: John Wiley & Sons, 2000.


Данная статья была создана в рамках учебного задания.
Студент: Юрий Янович
Преподаватель: В.В. Стрижов
Срок: 28 мая 2009


В настоящее время задание завершено и проверено. Данная страница может свободно правиться другими участниками проекта MachineLearning.ru.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://poligon.machinelearning.ru/wiki/index.php?title=%D0%A1%D1%82%D0%B0%D1%82%D0%B8%D1%81%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%BE%D1%82%D1%87%D0%B5%D1%82_%D0%BF%D1%80%D0%B8_%D1%81%D0%BE%D0%B7%D0%B4%D0%B0%D0%BD%D0%B8%D0%B8_%D0%BC%D0%BE%D0%B4%D0%B5%D0%BB%D0%B5%D0%B9»
Личные инструменты