Аппроксимация Лапласа (пример)

Материал из MachineLearning.

Текущая версия

Аппроксимация Лапласа - способ оценки параметров нормального распределения при аппроксимации заданной плотности вероятности.

Постановка задачи

Задана выборка — множество значений свободных переменных и множество соответствующих им значений зависимой переменной. Необходимо для выбранной регрессионной модели :

3-1 показать зависимость среднеквадратичной ошибки от значений параметров модели: ;

3-2 построить график и сделать аппроксимацию Лапласа для зависимости ;

3-3 найти расстояния между полученными зависимостями, используя расстояние Кульбака - Лейблера.

Описание алгоритма

При восстановлении регрессии рассматривалась следующая гипотеза порождения данных:

, где

В таком случае, при фиксированной модели f плотность вероятности появления данных равняется^[1]:

, где

- это функция регрессионных невязок, т.е. ;

- нормировачный коэффициент.

3-1. В заданной модели f, используя метод наименьших квадратов, находим оптимальное значение вектора параметров . Далее, фиксируем все параметры выбранной регрессионной модели (для определенности зададим им оптимальные значения) кроме одного (пусть этот незафиксированный параметр будет ). После чего, варьируя значение , строим искомую зависимость и график . Таким образом построена зависимость от одного параметра . Аналогично действуя, строится зависимость от большего количества параметров.

3-2. При аппроксимации Лапласа, полученную в пункте 3-1 функцию приближаем функцией многомерного нормального распределения . Воспользуемся нелинейной регрессионной моделью:

Другими словами, зная из пункта 3-1 значение (т.е. множество пар , где - вектор параметров i-го сэмпла), надо получить корреляционную матрицу .

Вначале, представляем элементы матрицы в виде вектора параметров. Далее, используя метод Ньютона-Гаусса,находим оптимальный вектора параметров (минимум суммы остаточных квадратов). Затем, делаем обратный переход от вектора параметров к матрице и получаем искомую корреляционную матрицу .

3-3. Расстояние Кульбака - Лейблера между двумя распределениями p(z) и q(z) равняется:

Вычислительный эксперимент

Обозначим плотность распределения SSE как , а его аппроксимация лапласа .

Во время вычислительного эксперимента SSE принимало достаточно большие значения (порядка ). Как следствие, p(y) принимало значения порядка 1, и аппроксимация Лапласа была некорректной. Поэтому, аппроксимация Лапласа применялась не к самому распределению p(y), а к ln(p(y)) (т.е. к -SSE c точностью до коэффициента).

Пример 1

Задуманная функция . Рассматривается линейная регрессионная модель с двумя параметрами: . и - оптимальное значение параметров (при которых SSE минимально).

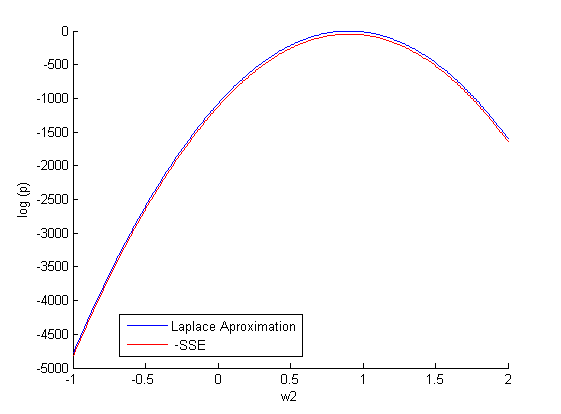
Фиксируем один параметр и задаем различные значение (500 случайных значений на отрезке [-1;2]). Строим зависимость:

.

Повторим эксперимент, только теперь варьируем сразу оба параметра и :

Рис. 1. Зависимость от и

Рис. 2. Зависимость от и . Ось log(p) направлена вверх

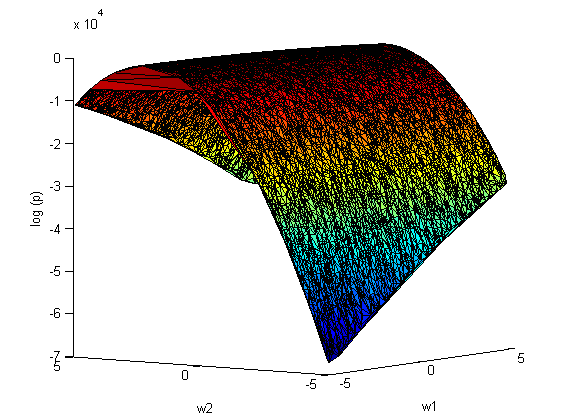
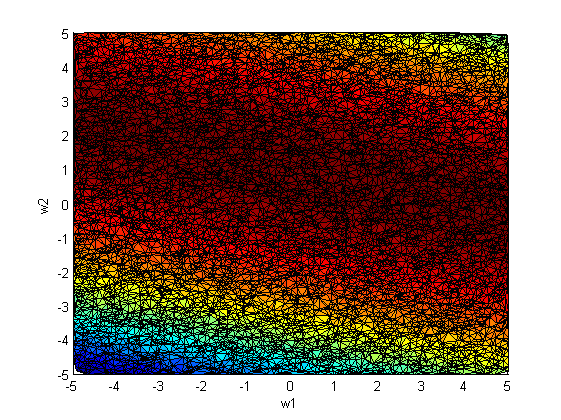
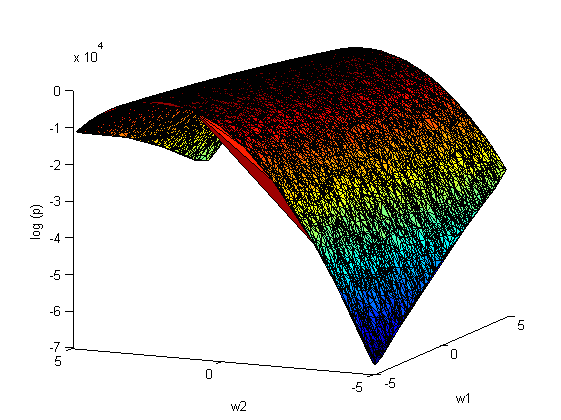
аппроксимация Лапласа:

Laplace approximation

ковариационная матрица FIXIT: матрица не является положительно определенной! По критерию Сильвестра элементы не диагонали должны быть положительны

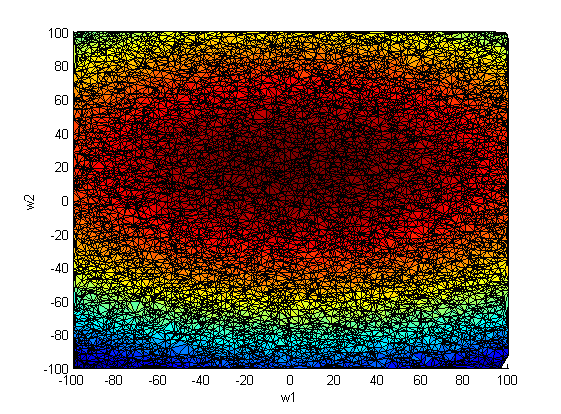
На рис.2 наблюдается зависимость между коэффициентами и . Следовательно, ковариационная матрица не будет диагональной.

Пример 2

Задуманная функция , где - белый гауссовский шум. Рассматривается следующая регрессионная модель: линейная комбинация функций и .

.

и - оптимальное значение параметров (при которых SSE минимально).

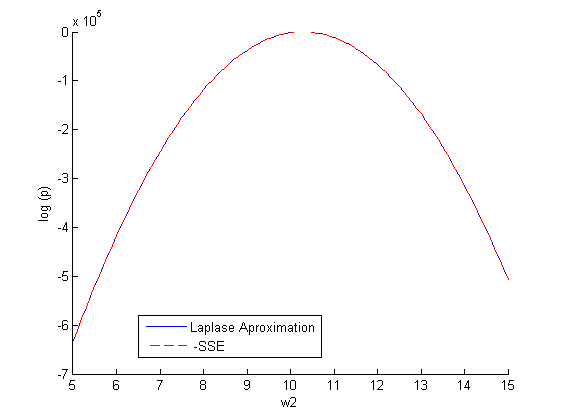
Фиксируем один параметр и задаем различные значение (10000 случайных значений на отрезке [5;15]). Строим зависимость:

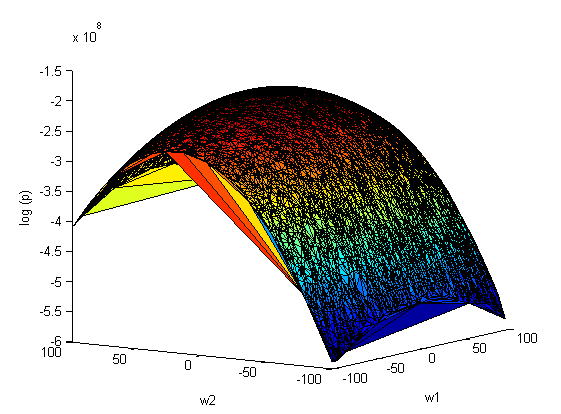
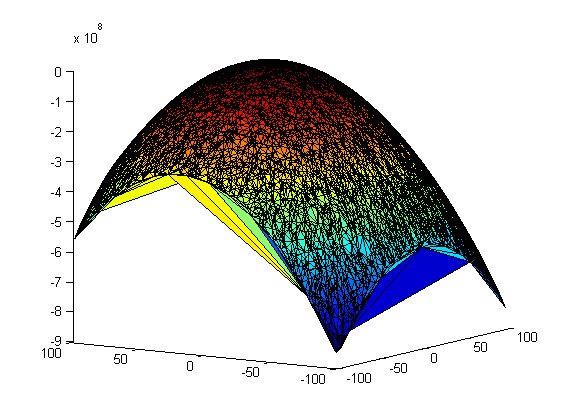
Повторим эксперимент, только теперь варьируем сразу оба параметра и (10000 случайных значений на отрезке [-100;100]):

Рис. 1. Зависимость от и

Рис. 2. Зависимость от и . Ось log(p) направлена вверх

аппроксимация Лапласа:

Laplace Approximation

Laplace Approximation. Ось log(p) направлена вверх

ковариационная матрица

Пример 3

Задуманная функция , где - белый гауссовский шум. Рассматривается существенно нелинейная регрессионная модель с двумя параметрами: .

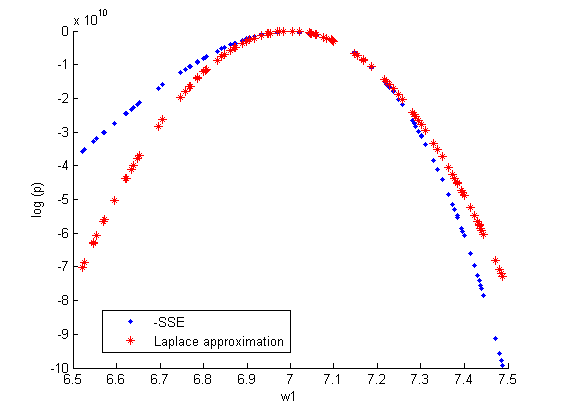
Фиксируем один параметр и задаем различные значение (10000 случайных значений на отрезке [6.5;7.5]). Строим зависимость:

.

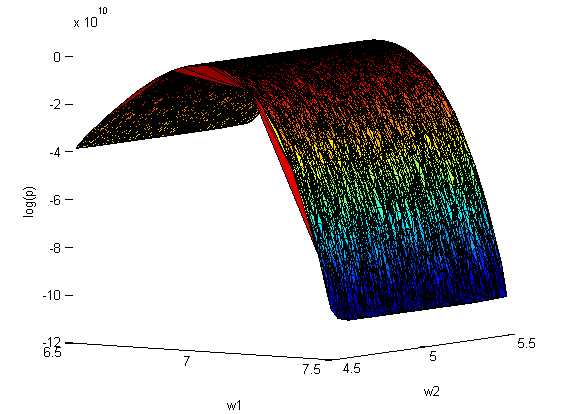
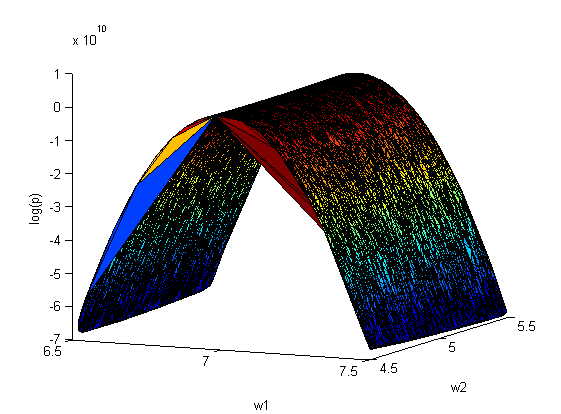
Повторим эксперимент, только теперь варьируем сразу оба параметра и (10000 случайных значений на отрезках [4.5;5.5] и [6.5;7.5] соответственно):

Зависимость от и

аппроксимация Лапласа:

Laplace Approximation

ковариационная матрица

Смотри также

• Аппроксимация Лапласа
• Сэмплирование
• Сэмплирование на вики
• Скачать код MATLAB можно здесь

Литература

• Bishop, C. Pattern Recognition And Machine Learning. Springer. 2006.

Примечания

Данная статья была создана в рамках учебного задания. Студент: Евгений Зайцев Преподаватель: В.В.Стрижов Срок: 24 декабря 2010 В настоящее время задание завершено и проверено. Данная страница может свободно правиться другими участниками проекта MachineLearning.ru. См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.