Участник:Gukov/Песочница
Материал из MachineLearning.
(→Рекомендации программисту) |
(→Введение) |
||
| Строка 1: | Строка 1: | ||
== Введение == | == Введение == | ||
| - | === | + | === Метод Ньютона-Рафсона === |
| + | {{main|Метод касательных (Ньютона-Рафсона)}} | ||
| - | + | Пусть имеется некоторая функция <tex>F(x)</tex> и необходимо найти такие значения аргумента <tex>x</tex>, для которых | |
| - | {{ eqno | 1}} | + | {{eqno|1}} |
| - | :<tex> | + | :<tex>F(x)=0</tex> |
| - | + | Перепишем {{eqref|1}} в виде | |
| - | <tex> | + | {{eqno|1.1}} |
| - | f(x) | + | :<tex>x = f(x)</tex> |
| - | </tex> | + | |
| - | {{ eqno | 2}} | + | и запишем <tex>n+1</tex>-ое приближения корня {{eqref|1.1}}, при этом делая поправку <tex>\alpha</tex> к очередному значению <tex>x_n</tex> |
| - | :<tex> | + | {{eqno|2}} |
| + | :<tex>x_{n+1} = x_n + \alpha \Delta x_n,</tex> | ||
| + | где <tex>\Delta x_n = f(x_n) - x_n,</tex> и положим <tex>\alpha = \frac{1}{1-f'(x_n)}</tex>. | ||
| - | + | Тогда {{eqref|2}} перепишется в виде | |
| - | + | {{eqno|3}} | |
| + | :<tex>x_{n+1} = \frac{f(x_n) - x_n f'(x_n)}{1 - f'(x_n)}</tex> | ||
| - | :<tex> | + | Нетрудно видеть, что {{eqref|3}} эквивалентно простому [[Метод последовательных приближений|методу последовательных приближений]] |
| + | :<tex>x_{n+1} = g(x_n),</tex> | ||
| + | где <tex>g(x) = \frac{f(x) - x f'(x)}{1 - f'(x)}</tex>. | ||
| - | + | Вспомним также, что если <tex>|g'(x)| < 1</tex>, то метод сходится. Имеем | |
| - | + | :<tex>g'(x) = \frac{f''(x)[f(x) - x]}{[1 - f'(x)]^2}.</tex> | |
| - | + | Но так как справедливо соотношение {{eqref|1.1}}, то для <tex>x,</tex> достаточно близких к решению {{eqref|1.1}}, выражение в скобках в числителе дроби становится малым. Поэтому итерационный метод, описываемый формулой {{eqref|3}} сходится, если | |
| + | * 1. Начальное приближение <tex>x_0</tex> выбрано достаточно близко к решению <tex>x = f(x)</tex>. | ||
| + | * 2. Производная <tex>f''(x)</tex> не становится слишком большой. | ||
| + | * 3. Производная <tex>f'(x)</tex> не слишком близка к 1. | ||
| - | + | Это и есть метод Ньютона-Рафсона. Обычно его записывают в виде | |
| + | {{eqno|4}} | ||
| + | :<tex>x_{n+1} = x_{n} - \frac{F(x_n)}{F'(x_n)}</tex>, | ||
| + | |||
| + | где <tex>F(x) = f(x) - x = 0</tex> | ||
| + | |||
| + | Таким образом, мы вернулись к уравнению в форме {{eqref|1}}, и условия сходимости принимают следующий вид | ||
| + | * 1. Начальное приближение <tex>x_0</tex> выбрано достаточно близко к корню уравнения <tex>F(x) = 0</tex>. | ||
| + | * 2. Производная <tex>F''(x)</tex> не становится очень большой. | ||
| + | * 3. Производная <tex>F'(x)</tex> не слишком близка к 0. | ||
| + | |||
| + | === Случай почти равных корней === | ||
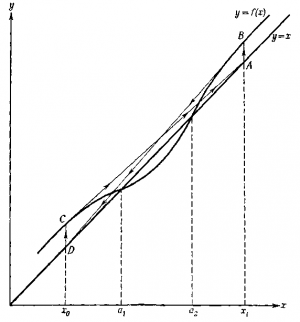
| + | Условие 3 сходимости метода Ньютона-Рафсона означает, что никакие два корня не находятся слишком близко один к другому. Соответствующая ситуация представлена на рисунке 1. [[Изображение:macon.png|thumb|300px]] | ||
== Изложение метода == | == Изложение метода == | ||
Версия 16:20, 18 ноября 2008
Содержание |
Введение
Метод Ньютона-Рафсона
Пусть имеется некоторая функция и необходимо найти такие значения аргумента
, для которых
Перепишем (1) в виде
и запишем -ое приближения корня (1.1), при этом делая поправку
к очередному значению
где и положим
.
Тогда (2) перепишется в виде
Нетрудно видеть, что (3) эквивалентно простому методу последовательных приближений
где .
Вспомним также, что если , то метод сходится. Имеем
Но так как справедливо соотношение (1.1), то для достаточно близких к решению (1.1), выражение в скобках в числителе дроби становится малым. Поэтому итерационный метод, описываемый формулой (3) сходится, если
- 1. Начальное приближение
выбрано достаточно близко к решению
.
- 2. Производная
не становится слишком большой.
- 3. Производная
не слишком близка к 1.
Это и есть метод Ньютона-Рафсона. Обычно его записывают в виде
,
где
Таким образом, мы вернулись к уравнению в форме (1), и условия сходимости принимают следующий вид
- 1. Начальное приближение
выбрано достаточно близко к корню уравнения
.
- 2. Производная
не становится очень большой.
- 3. Производная
не слишком близка к 0.
Случай почти равных корней
Условие 3 сходимости метода Ньютона-Рафсона означает, что никакие два корня не находятся слишком близко один к другому. Соответствующая ситуация представлена на рисунке 1.Изложение метода
Экстраполяция Ричардсона
Предположим, что для вычисления интеграла (1) отрезок разбит на
равных отрезков длины
и на каждом частичном отрезке применяется одна и та жа квадратурная формула. Тогда исходный интеграл
заменяется некоторой квадратурной суммой
, причем возникающая погрешность зависит от шага сетки
.
Для некоторых квадратурных формул удается получить разложение погрешности
по степеням
. Предположим,
что для данной квадратурной суммы
существует разложение:
,
где и коэффициенты
не зависят от
.
При этом величины
предполагаются известными.
Теперь предположим:
Чтобы избавиться от степени , составляющей ошибку (ибо среди всех слагаемых, составляющих ошибку, слагамое при
является наибольшим) вычислим величину
. Имеем:
Отсюда
то есть имеем более точное приближение к интегралу .
Таким образом, рекуррентную формулу можно записать в виде:
Заметим, что - величина, на которую мы делим размер шага при каждом новом вычислении
. Разумно положить
, т.к. большие значения
могут вызвать резкое увеличение количества вычислений.
Для наглядности представим процесс экстраполирования следующей таблицей:
Метод Рунге
Пусть существует асимптотическое разложение вида:
,
где - достаточно гладкая функция, а
.
Проведем расчеты на двух равномерных сетках с шагами и
соответственно и найдем выражения
и
,
. Потребуем,
чтобы погрешность для их линейной комбинации:
была величиной более высокого порядка по сравнению с и
. Если для
имеет место формула вида
,
то для
получим
Выберем параметр \sigma из условия :
.
Имеем
,
,
причем . Так, если
, то
. Таким образом, проведя вычисления на двух сетках
с шагами
и
, мы повысили порядок точности на
(на
) для
.
Процесс Эйткена
Метод расчета на нескольких сетках применяется для повышения порядка точности даже в том случае, когда неизвестен порядок главного члена погрешности. Предположим, чт для погрешности имеет место представление
,
,
так что
Проведем вычисления на трех сетках: ,
,
(
). Определим
. При этом пренебрегаем членом
. Образуем отношение
и найдем
.
Зная приближенное значение , можно методом методом Рунге повысить порядок точности. Для этого образуем комбинацию
и выберем
так, чтобы
, то есть
.
Тогда для погрешности
получаем
.
Числовой пример
Найдем с помощью квадратурной формулы трапеций приближенное значение интеграла, применив экстраполяцию Ричардсона (данный метод называется методом Ромберга):
В нижеследующей таблице представлены результаты работы программы:
| r | Исходная формула | Экстраполированная формула | Точное значение | Погрешность вычислений | Погрешность формулы |
|---|---|---|---|---|---|
| 2 | 3.98277278 | 4.04665506 | 4.04718956 | 0.0005345 | 0.00275556 |
| 4 | 4.03068449 | 4.04714980 | 4.04718956 | 0.00003976 | 0.00017222 |
| 8 | 4.04303347 | 4.04718692 | 4.04718956 | 0.00000264 | 0.00001076 |
| 16 | 4.04614856 | 4.04718939 | 4.04718956 | 0.00000017 | 0.00000067 |
| 32 | 4.04692918 | 4.04718955 | 4.04718956 | 0.00000001 | 0.00000004 |
| 64 | 4.04712446 | 4.04718956 | 4.04718956 | 0 | 0 |
| 20384 | 4.04718956 |
Здесь - коэффициент измельчения шага
. Исходная величина шага
.
На иллюстрации черная сплошная линия - исходная формула, красная пунктирная - экстраполированная.
Как мы видим, разница между экстраполированными и неэкстраполированными результатами значительна. Уже при величине шага в мы можем найти значение интеграла с точностью
, тогда как в исходной формуле нам для достижения такой точности пришлось бы задать величину шага
.
Рекомендации программисту
Программируя экстраполяцию Ричардсона следует предпочесть итерацию рекурсии. Также реализуя многократное экстраполирование итеративно, нам не нужно хранить всю таблицу значений - достаточно иметь в распоряжении два последних столбца.
Заключение
Мы получили более точные результаты при меньшем количестве вычислений функции, чем в исходном методе. Избавившись от степени, составляющей ошибку, мы пришли к результату, который в противном случае был бы недостижим без значительного уменьшения размера шага. Таким образом, мы преобразовали весьма посредственный алгоритм вычисления интегралов в довольно эффективный.
Список литературы
- А.А.Самарский, А.В.Гулин. Численные методы М.: Наука, 1989.
- Fundamental Methods of Numerical Extrapolation With Applications, mit.edu