Нейронная сеть Кохонена
Материал из MachineLearning.
м |
(→Геометрическая интерпретация) |
||
| Строка 28: | Строка 28: | ||
=== Геометрическая интерпретация === | === Геометрическая интерпретация === | ||
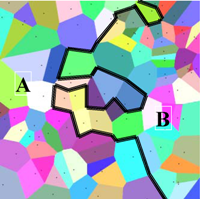
| - | [[Image:Coloured_Voronoi_2D. | + | [[Image:Coloured_Voronoi_2D.png|right|thumb|222px|Разбиение плоскости на многоугольники Вороного-Дирихле для случайно выбранных точек (каждая точка указана в своём многоугольнике).]] |
Большое распространение получили слои Кохонена, построенные следующим образом: каждому (<tex>j</tex>му) нейрону сопоставляется точка <tex>W_j = (w_{j1},...w_{jm})</tex> в <tex>m</tex>-мерном пространстве (пространстве сигналов). Для входного вектора <tex>x=(x_1,... x_m)</tex> вычисляется его расстояния <tex>\rho_j(x)</tex> до точек <tex>W_j</tex> и «ближайший получает всё» — тот нейрон, для которого это расстояние минимально, выдаёт единицу, остальные — нули. Следует заметить, что для сравнения расстояний достаточно вычислять линейную функцию сигнала: | Большое распространение получили слои Кохонена, построенные следующим образом: каждому (<tex>j</tex>му) нейрону сопоставляется точка <tex>W_j = (w_{j1},...w_{jm})</tex> в <tex>m</tex>-мерном пространстве (пространстве сигналов). Для входного вектора <tex>x=(x_1,... x_m)</tex> вычисляется его расстояния <tex>\rho_j(x)</tex> до точек <tex>W_j</tex> и «ближайший получает всё» — тот нейрон, для которого это расстояние минимально, выдаёт единицу, остальные — нули. Следует заметить, что для сравнения расстояний достаточно вычислять линейную функцию сигнала: | ||
: <tex>\rho_j(x)^2=\|x-W_j\|^2=\|W_j\|^2-2\sum_{i=1}^m w_{ji}x_i + \|x\|^2.</tex> | : <tex>\rho_j(x)^2=\|x-W_j\|^2=\|W_j\|^2-2\sum_{i=1}^m w_{ji}x_i + \|x\|^2.</tex> | ||
Версия 22:09, 9 сентября 2008
Нейронные сети Кохонена (Kohonen neural network) — класс нейронных сетей, основным элементом которых является слой Кохонена. Слой Кохонена состоит из адаптивных линейных сумматоров («линейных формальных нейронов»). Как правило, выходные сигналы слоя Кохонена обрабатываются по правилу «победитель забирает всё»: наибольший сигнал превращается в единичный, остальные обращаются в ноль.
По способам настройки входных весов сумматоров и по решаемым задачам различают много разновидностей сетей Кохонена.[1] Наиболее известные из них:
- Сети векторного квантования сигналов[1], тесно связанные с простейшим базовым алгоритмом кластеризации (метод динамических ядер или K-средних, то есть K-means)
- Самоорганизующиеся карты Кохонена (Self-Organising Maps, SOM)[1]
- Сети векторного квантования, обучаемые с учителем (Learning Vector Quantization)[1]
Содержание |
Слой Кохонена
Базовая версия
Слой Кохонена состоит из некоторого количества параллельно действующих линейных элементов. Все они имеют одинаковое число входов
и получают на свои входы один и тот же вектор входных сигналов
. На выходе
го линейного элемента получаем сигнал
где — весовой коэффициент
го входа
го нейрона,
— пороговой коэффициент.
После прохождения слоя линейных элементов сигналы посылаются на обработку по правилу «победитель забирает всё»: среди выходных сигналов ищется максимальный; его номер
. Окончательно, на выходе сигнал с номером
равен единице, остальные — нулю. Если максимум одновременно достигается для нескольких
, то либо принимают все соответствующие сигналы равными единице, либо только первый в списке (по соглашению). «Нейроны Кохонена можно воспринимать как набор электрических лампочек, так что для любого входного вектора загорается одна из них.»[1]
Геометрическая интерпретация
Большое распространение получили слои Кохонена, построенные следующим образом: каждому (му) нейрону сопоставляется точка
в
-мерном пространстве (пространстве сигналов). Для входного вектора
вычисляется его расстояния
до точек
и «ближайший получает всё» — тот нейрон, для которого это расстояние минимально, выдаёт единицу, остальные — нули. Следует заметить, что для сравнения расстояний достаточно вычислять линейную функцию сигнала:
Последнее слагаемое одинаково для всех нейронов, поэтому для нахождения ближайшей точки оно не нужно. Задача сводится к поиску номера наибольшего из значений линейных функций:
Таким образом, координаты точки совпадают с весами линейного нейрона слоя Кохонена (при этом значение порогового коэффициента
).
Если заданы точки , то
-мерное пространство разбивается на соответствующие многогранники Вороного-Дирихле
: многогранник
состоит из точек, которые ближе к
, чем к другим
(
).[1]
Сети векторного квантования
Задача векторного квантования с кодовыми векторами
для заданной совокупности входных векторов
ставится как задача минимизации искажения при кодировании, то есть при замещении каждого вектора из
соответствующим кодовым вектором. В базовом варианте сетей Кохонена используется метод наименьших квадратов и искажение
вычисляется по формуле
где состоит из тех точек
, которые ближе к
, чем к другим
(
). Другими словами,
состоит из тех точек
, которые кодируются кодовым вектором
.
Если совокупность задана и хранится в памяти, то стандартным выбором в обучении соответствующей сети Кохонена является метод K-средних. Это метод расщепления:
- при данном выборе кодовых векторов (они же весовые векторы сети)
минимизацией
находим множества
— они состоит из тех точек
, которые ближе к
, чем к другим
;
- при данном разбиении
на множества
минимизацией
находим оптимальные позиции кодовых векторов
— для оценки по методу наименьших квадратов это просто средние арифметические:
где — число элементов в
.
Далее итерируем. Этот метод расщепления сходится за конечное число шагов и даёт локальный минимум искажения.
Если же, например, совокупность заранее не задана, или по каким-либо причинам не хранится в памяти, то широко используется онлайн метод. Векторы входных сигналов
обрабатываются по одному, для каждого из них находится ближайший кодовый вектор («победитель», который «забирает всё»)
. После этого данный кодовый вектор пересчитывается по формуле
где — шаг обучения. Остальные кодовые векторы на этом шаге не изменяются.
Для обеспечения стабильности используется онлайн метод с затухающей скоростью обучения: если — количество шагов обучения, то полагают
. Функцию
выбирают таким образом, чтобы
монотонно при
и чтобы ряд
расходился, например,
.
Векторное квантование является намного более общей операцией, чем кластеризация, поскольку кластеры должны быть разделены между собой, тогда как совокупности для разных кодовых векторов
не обязательно представляют собой раздельные кластеры. С другой стороны, при наличии разделяющихся кластеров векторное квантование может находить их и по-разному кодировать.
Самоорганизующиеся карты Кохонена
Идея и алгоритм обучения
Задача векторного квантования состоит, по своему существу, в наилучшей аппроксимации всей совокупности векторов данных кодовыми векторами
. Самоорганизующиеся карты Кохонена также аппроксимируют данные, однако при наличии дополнительной структуры в совокупности кодовых векторов (англ. codebook). Предполагается, что априори задана некоторая симметричная таблица «мер соседства» (или «мер близости») узлов: для каждой пары
(
) определено число
(
) при этом диагональные элементы таблицы близости равны единице (
).
Векторы входных сигналов обрабатываются по одному, для каждого из них находится ближайший кодовый вектор («победитель», который «забирает всё»)
. После этого все кодовые векторы
, для которых
, пересчитываются по формуле
где — шаг обучения. Соседи кодового вектора — победителя (по априорно заданной таблице близости) сдвигаются в ту же сторону, что и этот вектор, пропорционально мере близости.
Чаще всего, таблица кодовых векторов представляется в виде фрагмента квадратной решётки на плоскости, а мера близости определяется, исходя из евклидового расстояния на плоскости.
Самоорганизующиеся карты Кохонена служат, в первую очередь, для визуализации и первоначального («разведывательного») анализа данных.[1] Каждая точка данных отображается соответствующим кодовым вектором из решётки. Так получают представление данных на плоскости («карту данных»). На этой карте возможно отображение многих слоёв: количество данных, попадающих в узлы (то есть «плотность данных»), различные функции данных и так далее. При отображении этих слоёв полезен аппарат географических информационных систем (ГИС). В ГИС подложкой для изображения информационных слоев служит географическая карта. Карта данных является подложкой для произвольного по своей природе набора данных. Она служит заменой географической карте там, где ее просто не существует. Принципиальное отличие в следующем: на географической карте соседние объекты обладают близкими географическими координатами, на карте данных близкие объекты обладают близкими свойствами. С помощью карты данных можно визуализировать данные, одновременно нанося на подложку сопровождающую информацию (подписи, аннотации, атрибуты, информационные раскраски).[1] Карта служит также информационной моделью данных. С её помощью можно заполнять пробелы в данных. Эта способность используется, например, для решения задач прогнозирования.
Самоорганизующиеся карты и главные многообразия
Идея самоорганизующихся карт очень привлекательна и породила массу обобщений, однако, строго говоря, мы не знаем, что мы строим: карта — это результат работы алгоритма и не имеет отдельного («объектного») определения. Есть, однако, близкая теоретическая идея — главные многообразия (principal manifolds).[1] Эти многообразия обобщают линейные главные компоненты. Они были введены как линии или поверхности, проходящие через «середину» распределения данных, с помощью условия самосогласованности: каждая точка на главном многообразии
является условным математическим ожиданием тех векторов
, которые проектируются на
(при условии
, где
— оператор проектирования окрестности
на
),
Самоорганизующиеся карты могут рассматриваться как аппроксимации главных многообразий и популярны в этом качестве[1].
Упругие карты
Метод аппроксимации многомерных данных, основанный на минимизации «энергии упругой деформации» карты, погружённой в пространство данных, был предложен А. Н. Горбанём в 1996 году, и впоследствии развит им совместно с А. Ю. Зиновьевым, А. А. Россиевым и А. А. Питенко.[1] Метод основан на аналогии между главным многообразием и эластичной мембраной и упругой пластиной. В этом смысле он является развитием классической идеи сплайна (хотя упругие карты и не являются многомерными сплайнами).
Пусть задана совокупность входных векторов . Так же, как и сети векторного квантования и самоорганизующиеся карты, упругая карта представлена как совокупность кодовых векторов (узлов)
в пространстве сигналов. Множество данных
разделено на классы
, состоящие из тех точек
, которые ближе к
, чем к другим
(
). Искажение кодирования
может трактоваться как суммарная энергия пружин единичной жёсткости, связывающих векторы данных с соответствующими кодовыми векторами.
На множестве узлов задана дополнительная структура: некоторые пары связаны «упругими связями», а некоторые тройки объединены в «рёбра жёсткости». Обозначим множество пар, связанных упругими связями, через , а множество троек, составляющих рёбра жёсткости, через
. Например, в квадратной решётке ближайшие узлы (как по вертикали, так и погоризонтали) связываются упругими связями, а ребра жёсткости образуются вертикальными и горизонтальными тройками ближайших узлов. Энергия деформации карты состоит из двух слагаемых:
- энергия растяжения
- энергия изгиба
где — соответствующие модули упругости.
Задача построения упругой карты состоит в минимизации функционала
Если разбиение совокупности входных векторов на классы
фиксировано, то минимизация
— линейная задача с разреженной симметричной матрицей коэффициентов. Поэтому, как и для сетей векторного квантования, применяется метод расщепления: фиксируем
— ищем
— для данных
ищем
— для данных
ищем
— …
Алгоритм сходится к (локальному) минимуму
.
Метод упругих карт позволяет решать все задачи, которые решают самоорганизующиеся карты Кохонена, однако обладает большей регулярностью и предсказуемостью. При увеличении модуля изгиба упругие карты приближаются к линейным главным компонентам. При уменьшении обоих модулей упругости они превращаются в Кохоненовские сети векторного квантования. В настоящее время упругие карты интенсивно используются для анализа многомерных данных в биоинформатике.[1] Соответствующее программное обеспечение опубликовано и свободно доступно на сайте Института Кюри (Париж).[1][1]
Сети векторного квантования, обучаемые с учителем
Решается задача классификации. Число классов может быть любым. Изложим алгоритм для двух классов, и
. Исходно для обучения системы поступают данные, класс которых известен. Задача: найти для класса
некоторое количество
кодовых векторов
, а для класса
некоторое (возможно другое) количество
кодовых векторов
таким образом, чтобы итоговая сеть Кохонена с
кодовыми векторами
,
(объединяем оба семейства) осуществляла классификацию по следующему решающему правилу:
- если для вектора входных сигналов
ближайший кодовый вектор («победитель», который в слое Кохонена «забирает всё») принадлежит семейству
, то
принадлежит классу
; если же ближайший к
кодовый вектор принадлежит семейству
, то
принадлежит классу
.
С каждым кодовым вектором объединённого семейства связан многогранник Вороного-Дирихле. Обозначим эти многогранники
,
соответственно. Класс
в пространстве сигналов, согласно решающему правилу, соответствует объединению
, а класс
соответствует объединению
. Геометрия таких объединений многогранников может быть весьма сложной (см. Рис с примером возможного разбиения на классы).
Правила обучения сети онлайн строится на основе базового правила обучения сети векторного квантования. Пусть на вход системы подаётся вектор сигналов , класс которого известен. Если он классифицируется системой правильно, то соответствующий
кодовый вектор
слегка сдвигается в сторону вектора сигнала («поощрение»)
Если же классифицируется неправильно, то соответствующий
кодовый вектор
слегка сдвигается в противоположную сторону от сигнала («наказание»)
где — шаг обучения. Для обеспечения стабильности используется онлайн метод с затухающей скоростью обучения. Возможно также использование разных шагов для «поощрения» правильного решения и для «наказания» неправильного
Это — простейшая (базовая) версия метода[1]. Существует множество других модификаций.