Статистический анализ данных (курс лекций, К.В.Воронцов)/2013

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
м (→Оценки)
м (→Оценки)
Строка 51: Строка 51:
* Студенты, не получившие баллы за рецензии, могут набрать их, выкладывая в Matlab File Exchange реализации отсутствующих методов, описанных в курсе, или создавая на machinelearning.ru отсутствующие статьи о методах, описанных в курсе.
* Студенты, не получившие баллы за рецензии, могут набрать их, выкладывая в Matlab File Exchange реализации отсутствующих методов, описанных в курсе, или создавая на machinelearning.ru отсутствующие статьи о методах, описанных в курсе.
* Первая пересдача — 28.01. Дедлайн выполнения заданий к ней — '''23:59 11.01'''. Если первое задание было выполнено, переделывать его не нужно. Рецензирование не производится, но баллы за написание статей получить можно.
* Первая пересдача — 28.01. Дедлайн выполнения заданий к ней — '''23:59 11.01'''. Если первое задание было выполнено, переделывать его не нужно. Рецензирование не производится, но баллы за написание статей получить можно.
-
* Вторая пересдача — 11.02. Дедлайн выполнения заданий к ней — '''23:59 28.01'''. Если первое задание было выполнено, переделывать его не нужно. Рецензирование не производится, но баллы за написание статей получить можно.
+
* Вторая пересдача — 11.02. Дедлайн выполнения заданий к ней — '''23:59 28.01'''.
= Задание 1. Исследование свойств одномерных статистических критериев на модельных данных =
= Задание 1. Исследование свойств одномерных статистических критериев на модельных данных =

Версия 12:27, 28 января 2014

Содержание

Оценки

Студент #1 (1 балл) #2 (2 балла) Рецензирование #2 (1 балл) #3 (2 балла) Рецензирование #3 (1 балл) Другое (2 балла) Сумма (7 баллов) Максимальный итоговый балл Экзамен
Березин Алексей 1 2 1 (Нижибицкий) 2 1 (Куракин) 7 5 5
Борисов Михаил 1 0.5 0.4 2 3.9 3 3
Гавриков Михаил 1 2 1 (Потапенко) 2 (Лобачева) 1 7 5 5
Зак Евгений 0.8 2 0.9 (Фонарев) 2 5.7 4 4
Исмагилов Тимур 0 н/д
Кондрашкин Дмитрий 0.9 1.9 1 (Березин) 2 1 (Нижибицкий) 6.8 5 5
Куракин Александр 1 1.6 2 1 (Гавриков) 1 6.6 5 5
Лобачева Екатерина 1 1.8 1 (Остапец) 1.4 1 (Зак) 0.1 6.3 5 5
Любимцева Мария 1 1.8 2 2 6.8 5 5
Малышева Екатерина 1 2 2 2 7 5 5
Меркулова Татьяна 1 1 н/д
Морозова Дарья 0.6 1.6 1.1 3.5 3 3
Нижибицкий Евгений 1 2 (Кондрашкин) 2 1 (Потапенко) 1 7 5 5
Новиков Максим 1 1 н/д
Огнева Дарья 1 0 2 2 5 4 4
Остапец Андрей 1 2 1 (Гавриков) 2 1 (Березин) 7 5 5
Потапенко Анна 1 2 1 (Лобачева) 1.9 1 (Остапец) 6.9 5 5
Ромов Петр 0.9 0.9 н/д
Фонарев Александр 1 1.2 1 (Кондрашкин) 2 5.2 4 4
Шаймарданов Ильдар 1 1 н/д
  • Итоговая оценка определяется по формуле \min\left(5/7*Homework, Exam\right), где Homework — сумма баллов за домашние работы, Exam — оценка на устном экзамене. Округление делается по стандартным правилам.
  • Штраф за просрочку сдачи заданий начисляется из расчета 0.1 балла за сутки.
  • Задание считается сданным на момент получения проверяющим письма с отчётом (и кодом, если это указано в задании), при условии отсутствия необходимости внесения дополнений и исправлений.
  • Для допуска к экзамену необходимо сдать как минимум два задания, обязательно включая первое.
  • Балл за рецензирование можно получить только при условии сдачи соответствующего задания.
  • Студенты, не получившие баллы за рецензии, могут набрать их, выкладывая в Matlab File Exchange реализации отсутствующих методов, описанных в курсе, или создавая на machinelearning.ru отсутствующие статьи о методах, описанных в курсе.
  • Первая пересдача — 28.01. Дедлайн выполнения заданий к ней — 23:59 11.01. Если первое задание было выполнено, переделывать его не нужно. Рецензирование не производится, но баллы за написание статей получить можно.
  • Вторая пересдача — 11.02. Дедлайн выполнения заданий к ней — 23:59 28.01.

Задание 1. Исследование свойств одномерных статистических критериев на модельных данных

Необходимо провести исследование одного или нескольких классических критериев проверки статистических гипотез. Интерес представляет поведение достигаемого уровня значимости (p-value) как функции размера выборок и параметров распределения. В соответствии с индивидуальными параметрами задания необходимо указанным способом сгенерировать одну или несколько выборок из заданного распределения, выполнить проверку гипотезы при помощи соответствующего критерия, а затем многократно повторить эту процедуру для различных значений параметров. По результатам расчётов необходимо построить требуемые в задании графики, среди которых могут быть следующие:

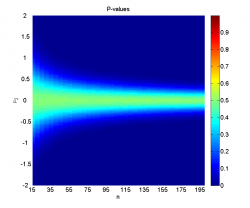
  1. график зависимости достигаемого уровня значимости от значений параметров при однократном проведении эксперимента;
  2. график зависимости достигаемого уровня значимости одного или двух критериев от значений параметров, усреднённого по большому количеству повторений эксперимента (например, по 1000 повторений);
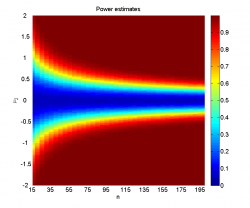
  3. график с эмпирическими оценками мощности одного или двух критериев для разных значений параметров.

В качестве оценки мощности принимается доля отвержений нулевой гипотезы среди всех проверок. То есть, если эксперимент повторялся k раз для каждого набора значений параметров, и в m из k случаев гипотеза была отвергнута на некотором фиксированном уровне значимости \alpha (примем \alpha=0.05), оценкой мощности будет отношение m/k.

Необходимо сдать: выполненный в Tex или Microsoft Word отчёт с описанием алгоритма, построенными графиками и выводами (объяснение полученных результатов моделирования, границы применимости критерия и т.д.), а также код на R, Матлабе или Питоне, при запуске которого на экран выводятся графики, соответствующие имеющимся в отчёте.

Задание принимается до 23:59 19.10.

Пример задания

Исследуем чувствительность классического двухвыборочного критерия Стьюдента для проверки гипотезы однородности против альтернативы сдвига при зашумлении выборок наблюдениями, взятыми из равномерного распределения.

X_1^n, \;\; X_{1i} \sim 0.9\cdot N(\mu_1,1)+ 0.1\cdot U\left[-5+\mu_1,5+\mu_1\right] — выборка длины n из смеси стандартного нормального N(\mu_1,1) и равномерного U\left[-5+\mu_1,5+\mu_1\right] распределений с весами 0.9 и 0.1 соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит 0.9, то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного).

X_2^n, \;\; X_{2i} \sim 0.9\cdot N(\mu_2,1)+ 0.1\cdot U\left[-5+\mu_2,5+\mu_2\right] — аналогичная выборка.

H_0\,:\; \mu_1=\mu_2, \;\; H_1\,:\; \mu_1\neq\mu_2.

\mu_1=0, \;\; \mu_2=-2\,:\,0.01\,:\,2, \;\; n=15\,:\,5\,:\,200.

При каждом значении \mu_2 выборки для разных значений n генерируются независимо.

Значения достигаемого уровня значимости при однократной генерации выборок.

Значения достигаемого уровня значимости, усрёднённые по 3000 экспериментам.

Значения эмпирических оценок мощности критерия при проведении 3000 экспериментов (\alpha=0.05).

Заметим, что однократная генерация выборок даёт достаточно нестабильные результаты, не позволяя точно оценить границы области, где нулевая гипотеза отклоняется, поэтому и необходимо усреднение по большому числу экспериментов.

Видно, что при достаточно большой разнице между средними и большом размере выборок наличие шума не мешает уверенно отклонять гипотезу однородности. Когда, наоборот, разница между средними невелика (меньше 0.2-0.5 в зависимости от размера выборок), мощность близка к нулю, а среднее значение достигаемого уровня значимости колеблется около 0.5, что логично, так как его распределение при справедливости нулевой гипотезы равномерно на [0,1].

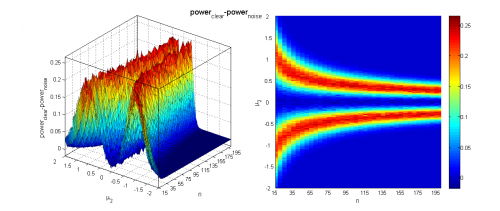
Чтобы оценить вклад зашумления выборок, оценим при всех значениях параметра мощность критерия и средний достигаемый уровень значимости на аналогичных выборках без шума и сравним результаты.

Разность средних достигаемых уровней значимости на выборках без шума и с шумом.

Разность эмпирических оценок мощности на выборках без шума и с шумом.

Видно, что наличие шума всё меньше влияет на работу критерия с ростом объёма выборок и разницы между их средними. Тем не менее, в некоторых областях изменения параметров потеря мощности из-за 10% зашумления может составлять до 20%, а средний достигаемый уровень значимости может быть выше на 0.1.

Отметим, что приведённые количественные выводы справедливы только для шума рассматриваемой структуры.

Задания

Анализ поведения схожих критериев

Требуется исследовать поведение указанной пары статистических критериев, подходящих для решения одной и той же задачи, сравнить мощность и достигаемые уровни значимости и сделать выводы о границах применимости критериев. Необходимо для каждого из критериев построить графики зависимости достигаемых уровней значимости и оценок мощностей от параметров, и показать, в каких областях изменения параметров предпочтительнее использовать тот или иной критерий. Для получения более гладких графиков рекомендуется применять оба критерия к одним и тем же выборкам, а не генерировать их отдельно для каждого критерия.

  • X^n, \;\; X_i\sim Ber(p);
    H_0\,:\, p=\frac{1}{2}, \;\; H_1\,:\, p\neq\frac{1}{2};
    p=0.01\,:\,0.01\,:\,0.99, \;\; n=5\,:\,1\,:\,50.
Гавриков: сравнить Z-критерий и точный критерий для доли.
Потапенко: сравнить критерии, основанные на доверительных интервалах Вальда и Уилсона (нулевая гипотеза отвергается на уровне значимости 5%, если 95% доверительный интервал для параметра не содержит \frac{1}{2}).
  • X^n, \;\; X_i\sim N(\mu,\sigma);
    H_0\,: среднее значение X равно нулю, H_1\,: среднее значение X не равно нулю;
    \mu=-2\,:\,0.01\,:\,2, \;\; \sigma=1, \;\; n=5\,:\,1\,:\,50.
Нижибицкий: сравнить одновыборочные T- и Z-критерии.
Зак: сравнить критерий знаковых рангов Уилкоксона и одновыборочный перестановочный критерий с суммой элементов в качестве статистики.
  • X_1^{n}, \;\; X_{1i} \sim N(\mu_1, \sigma_1^2),\;\;X_2^{n}, \;\; X_{2i} \sim N(\mu_2, \sigma_2^2);
    H_0\,: средние выборок равны, \;H_1\,: средние выборок не равны;
    \mu_1=0, \;\; \sigma_1=1.
Остапец: \mu_2=-2\,:\,0.02\,:\,2, \;\; \sigma_2 = 0.5\,:\,0.01\,:\,2, \;\; n=30. Сравнить критерий Стьюдента для неизвестных равных дисперсий и двухвыборочный перестановочный критерий, основанный на статистике критерия Стьюдента для неизвестных равных дисперсий.
Морозова: \mu_2=-2\,:\,0.02\,:\,2, \;\; \sigma_2 = 1, \;\; n=5\,:\,1\,:\,50. Сравнить критерий Аспина-Уэлша и двухвыборочный перестановочный критерий с разностью средних в качестве статистики.
Шаймарданов: \mu_2=-2\,:\,0.02\,:\,2, \;\; \sigma_2 = 1, \;\; n=5\,:\,1\,:\,50. Сравнить критерий Уилкоксона-Манна-Уитни и критерий знаков.
  • X_1^n, \;\; X_{1i} \sim 0.5\cdot N(0,1)+ 0.5\cdot U\left[-a,a\right], \;\; X_2^n, \;\; X_{2i} \sim 0.5\cdot N(0,\sigma^2)+ 0.5\cdot U\left[-a,a\right] — выборки длины n из смеси нормального и равномерного U\left[-a,a\right] распределений с равными весами (при генерации выборки используется случайный датчик — если его значение не превосходит 0.5, то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного).
    H_0\,: дисперсии двух выборок равны, \;H_1\,: дисперсии двух выборок не равны;
    \sigma=0.1\,:\,0.05\,:\,4.
Кондрашкин: a=3, \;\; n=10\,:\,5\,:\,100. Сравнить критерий Зигеля-Тьюки и критерий Брауна-Форсайта.
Борисов: a=0.5\,:\,0.1\,:\,5, \;\; n=50. Сравнить критерий Брауна-Форсайта и критерий Фишера.
Огнева: a=5, \;\; n=5\,:\,1\,:\,50. Сравнить WM-критерий и перестановочный критерий, основанный на статистике Али.
  • X^n, \;\; X_i \sim p\cdot N(0,1)+ \left(1-p\right)\cdot U\left[-a,a\right] — выборка длины n из смеси стандартного нормального N(0,1) и равномерного U\left[-a,a\right] распределений с весами p и 1-p соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит p, то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного).
    H_0\,:\; X_i \sim N, \;\;\; H_1\,:\; H_0 неверна;
    n=10\,:\,5\,:\,100.
Фонарев: a=1, \;\; p=0\,:\,0.02\,:\,1. Сравнить критерий Шапиро-Уилка и критерий Колмогорова-Смирнова.
Лобачева: a=2, \;\; p=0\,:\,0.02\,:\,1. Сравнить критерий омега-квадрат и критерий Жарка-Бера.
Исмагилов: a=0.5\,:\,0.1\,:\,5, \;\; p=0.25. Сравнить критерий Колмогорова-Смирнова и критерий хи-квадрат.

Анализ устойчивости критериев к нарушению предположений

Требуется исследовать поведение указанного критерия в условиях нарушения лежащих в его основе предположений. Оценить мощность и достигаемый уровень значимости критерия при различных значениях параметров, сделать выводы об устойчивости

X^n, \;\; X_i \sim p\cdot N(\mu,1)+ \left(1-p\right)\cdot U\left[-a+\mu,a+\mu\right] — выборка длины n из смеси нормального N(\mu,1) и равномерного U\left[-a+\mu,a+\mu\right] распределений с весами p и 1-p соответственно (при генерации каждой выборки используется случайный датчик — если его значение не превосходит p, то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного).
H_0\,:\; \mu=0, \;\; H_1\,:\; \mu\neq0.

Березин: \mu=-2\,:\,0.01\,:\,2, \;\; p=0.8, \;\; a=1, \;\; n=15\,:\,5\,:\,200.
Малышева: \mu=1, \;\; p=0\,:\,0.01\,:\,1, \;\; a=2, \;\; n=15\,:\,5\,:\,200.
Ромов: \mu=-2\,:\,0.01\,:\,2, \;\; p=0\,:\,0.01\,:\,1, \;\; a=1, \;\; n=150.
Новиков: \mu=0.5, \;\; p=0\,:\,0.01\,:\,1, \;\; a=0.1\,:\,0.1\,:\,5, \;\; n=100.
  • Критерий Фишера для проверки равенства дисперсий, нарушение предположения о нормальности.

X_1^n, \;\; X_{1i} \sim p_1\cdot N(0,\sigma_1^2)+ \left(1-p_1\right)\cdot U\left[-a,a\right] — выборка длины n из смеси нормального N(0,\sigma_1^2) и равномерного U[-a,a] распределений с весами p_1 и 1-p_1 соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит p_1, то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного),
X_2^n,\;\; X_{2i} \sim p_2\cdot N(0,\sigma_2^2)+ \left(1-p_2\right)\cdot U\left[-a,a\right] — аналогичная выборка,
H_0\,: дисперсии двух выборок равны, \;H_1\,: дисперсии двух выборок не равны;
\sigma_1=2, \;\; \sigma_2=0.1\,:\,0.05\,:\,4.

Куракин: p_1=p_2=0.8, \;\; a=2, \;\; n=15\,:\,5\,:\,200.
Любимцева: p_1=p_2=0\,:\,0.01\,:\,1, \;\; a=3, \;\; n=100.

Задания 2 и 3. Анализ реальных данных

Ниже приведены описания анализируемых данных и постановки задач. При проведении анализа можно пользоваться любыми доступными программными средствами. Необходимо предоставить подробный письменный отчёт по проведённому исследованию, содержащий визуализацию исходных данных, описания и выводы каждого этапа анализа — используемые методы, обоснование их применимости, промежуточные результаты вычислений, графики. Особое внимание необходимо обращать на полноту применения методов. Помимо выводов, касающихся математических особенностей решения, необходимо включить в отчёт заключения, сформулированные в терминах предметной области, которые могли бы быть понятны гипотетическому заказчику-нематематику.

Задание 2

Отчёт каждого студента рецензируется назначенным одногруппником. Задачей рецензента является проверка корректности выбора метода решения, полноты его применения и понятности изложения. Рецензент получает баллы, если рецензируемая им работа была принята с первого раза, при условии, что его собственная работа также сдана.

Предварительные версии отчётов принимаются до 23:59 23.11, финальные, по результатам работы с рецензентом — до 23:59 30.11.

Интеллект и размер головного мозга

Исследование проводилось среди студентов психологического факультета крупного университета. Все испытуемые должны были быть правшами, а также не иметь повреждений мозга, эпилепсии, алкоголизма и сердечных заболеваний. Участники предварительного этапа эксперимента прошли несколько IQ-тестов, после чего для дальнейшего участия было отобрано 20 мужчин и 20 женщин, имевших коэффициент интеллекта либо ниже 103, либо выше 130 баллов. Для каждого из отобранных при помощи магнитно-резонансной томографии были получены 18 снимков срезов головного мозга, и общее количество пикселей на всех 18 снимках было принято в качестве меры объёма мозга. Помимо этого, были собраны данные о росте и массе тела испытуемых.

Лобачева: проанализировать, какие из факторов значимо влияют на объём головного мозга. Проверить, по какой из двух групп факторов можно предсказывать объём головного мозга с большей уверенностью – по результатам тестов интеллекта, или по полу, росту и весу.

Стоимость подержанных автомобилей

Имеются данные о стоимости 804 подержанных автомобилей и их характеристиках: известны пробег, производитель, модель, вид модели, тип кузова, число цилиндров, объём двигателя, число дверей, а также наличие или отсутствие круиз контроля, продвинутой звуковой системы и кожаной обивки сидений.

Фонарев: построить модель стоимости автомобиля по данному набору признаков.

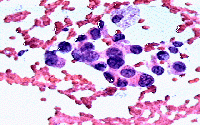
Клетки опухолей груди

Гистохимия пунктата злокачественной опухоли.
Гистохимия пунктата злокачественной опухоли.

357 испытуемым с доброкачественными и 212 со злокачественными опухолями груди была сделана тонкоигольная аспирационная пункция с гистологическим исследованием пунктата. По полученным изображениям определялись следующие признаки опухолевых клеток: радиус, однородность текстуры, периметр, площадь, гладкость, компактность, степень вогнутости, доля вогнутых участков контура, симметричность, фрактальная размерность. Для каждого изображения были рассчитаны среднее значение каждого из этих признаков, стандартное отклонение и среднее по трём клеткам с максимальным значением признака.

Ромов: оценить вероятность того, что опухоль злокачественная, по набору рассчитанных по изображению признаков. Построить функции, дающие точечную оценку и границы 95% доверительного интервала. Подобрать порог на вероятность для классификации.

Пожертвования на благотворительность

Благотворительная организация разослала 4268 писем с предложением сделать пожертвование и получила отклик с пожертвованиями от 1707 адресатов. Для каждого адресата известны: индикатор ответа на предыдущее письмо, число недель, прошедших с момента предыдущего пожертвования, размеры текущего, предыдущего и среднего по всем предыдущим пожертвованиям в голландских гульденах, число писем, отправляемых адресату в год, доля писем, в ответ на которые приходят пожертвования.

Потапенко: построить функцию, оценивающую вероятность получения пожертвования от адресата по историческим данным.

Концентрация озона

Имеются данные измерений состояния атмосферы, произведённых в Нью-Йорке в течение 111 подряд идущих дней. Измерены температура воздуха, скорость ветра, уровень солнечной радиации и концентрация озона.

Березин: построить функцию, по имеющимся признакам оценивающую наиболее вероятное значение концентрации озона и доверительный интервал для него.

Эффективность тромболитической терапии

Собраны данные по 206 пациентам второго кардиологического отделения московской городской клинической больницы №25. Имеются результаты 14 анализов, а также 8 дополнительных признаков, описывающих пациента (пол, возраст, курение, наличие диабета и т. д.)

Зак: построить функцию, оценивающую вероятность выздоровления пациента в результате тромболитической терапии по приведённым 22 признакам.
Огнева: построить функцию, оценивающую вероятность возникновения осложнений у пациента в результате тромболитической терапии по приведённым 22 признакам.

Генетически модифицированные мыши с синдромом Дауна

Эмбрионы мышей с внедрённой копией участка 21-й хромосомы человека (слева) и без (справа).
Эмбрионы мышей с внедрённой копией участка 21-й хромосомы человека (слева) и без (справа).

Синдром Дауна — геномная патология, характеризующаяся наличием дополнительной копии генетического материала по 21-й хромосоме. В целях исследования болезни Дауна была создана популяция мышей с внедрённой копией одного из участков 21-й хромосомы человека. Первому поколению мышей внедрялся один из четырёх участков, затем они скрещивались с немодифицированными мышами, и внедрённый участок мог передаваться потомкам. Все они оказались слепыми, поэтому невозможно было провести прямую проверку уровня их интеллекта. Для 500 особей известны: наименование внедрённого участка хромосомы (A=141G6; B=152F7; C=230E8; D=285E6), номер линии мышей (мыши, произошедшие от одной и той же трансгенной особи, относятся к одной линии), пол особи, вес, возраст, в котором он был измерен, номер клетки, в которой жила особь, а также индикатор содержания в её ДНК человеческого материала.

Гавриков: люди, страдающие болезнью Дауна, более склонны к ожирению; справедливо ли это для генетически модифицированных мышей? Исследовать различия с учётом всех остальных факторов.

Продолжительность жизни и активность размножения самцов дрозофилы

Для изучения влияния активности размножения самцов дрозофилы на продолжительность их жизни был организован следующий эксперимент. По 25 самцов в пяти группах содержались в одинаковых условиях, за исключением одного отличия: в первой группе к каждому самцу ежедневно подсаживалась готовая к размножению самка, во второй — восемь готовых к размножению самок, в третьей и четвёртой — соответственно, одна и восемь беременных самок, не готовых к размножению, наконец, к самцам четвёртой группы не подсаживали никого. Для каждого самца измерена продолжительность жизни, длина грудной клетки и доля времени, проводимого во сне.

Кондрашкин: построить функцию, предсказывающую продолжительность жизни самца дрозофилы в зависимости от условий его содержания, дать интерпретацию вклада признаков.

Счета за электроэнергию

Имеются помесячные данные о тратах на электроэнергию одного фиксированного домохозяйства на среднем западе США. За каждый месяц 1991-2000 годов приведены затраты на электроэнергию в долларах. Для объяснения колебаний размера счёта приведены следующие переменные: среднемесячная температура по данным последних тридцати лет, погодные индексы CDD и HDD (CDD — Cooling Degree Day — количество градусов, на которые средняя дневная температура больше 65°F, взятое суммой за все дни месяца; HDD — Heating Degree Day — аналогично, суммарное количество градусов, на которое средняя дневная температура меньше 65°F), число проживающих в доме членов семьи, индикатор установки нового счётчика, индикаторы установки двух новых тепловых насосов, объём потребления электроэнергии в киловатт-часах.

Борисов: построить функцию, предсказывающую затраты на электроэнергию по температуре, погодным индексам и числу проживающих в доме.

Состав бетона

Для 103 образцов раствора бетона известно содержание в кубическом метре семи основных компонент, для каждого образца измерены также осадка, растекание и прочность на сжатие.

Куракин: построить функцию, оценивающую растекание бетона по его составу.
Малышева: построить функцию, оценивающую прочность бетона на сжатие по всем имеющимся характеристикам, оценить вклад растекания и осадки.

Внешний вид и привлекательность самок мечехвостов

Мечехвосты (Limulus polyphemus).
Мечехвосты (Limulus polyphemus).

Изучалось влияние внешних характеристик самок морских ракообразных мечехвостов на их привлекательность для самцов. Выборка состоит из данных о наблюдениях над 173 особями и содержит закодированные данные о размере самок, их весе, цвете, состоянии панциря, а также о количестве спутников.

Нижибицкий: построить функцию, по внешним параметрам самки предсказывающую, будет ли у неё хотя бы один спутник; интерпретировать вклад каждого фактора.

Массовая доля жира в организме

Массовая доля жира, важная характеристика здоровья, рассчитывается через плотность тела, измеряемую при помощи взвешивания в воде. Для 252 мужчин проведены такие расчёты. Имеются также данные антропометрии (возраст, рост, вес, обхват грудной клетки и т. д.)

Морозова: построить функцию, оценивающую индекс ожирения без использования данных взвешивания.

Вкус португальского вина

Для 1599 образцов красного и 4898 белого португальского вина известны оценки (от 0 до 10), выставленные дегустаторами при слепом тестировании, а также значения одиннадцати биохимических показателей, полученных при лабораторном анализе.

Остапец: построить модель экспертной оценки красного вина по биохимическим характеристикам, оценить влияние содержания алкоголя на экспертную оценку.
Меркулова: построить функцию, оценивающую вероятность того, что вино, для которого известны биохимические характеристики и экспертная оценка, является красным, и доверительный интервал для неё. Оценить влияние экспертной оценки на эту вероятность.

Преступность и демографические характеристики

Данные собраны из переписи населения США 1990 года, отчёта ФБР о преступности за 1995 год и опроса сотрудников полиции LEMAS за 1990 год. По 2215 округам имеется статистика преступлений и 125 демографических показателей.

Любимцева: построить функцию, оценивающую число поджогов на сто тысяч населения по демографическим показателям, дать интерпретацию модели.

Задание 3

В отчёте должны содержаться:

  • визуальный анализ данных, оценка наличия выбросов и необходимости преобразований, анализ наличия тренда и сезонности;
  • построение моделей ряда (EST, ARIMA), обоснование выбора моделей и настройки их параметров, проверка предположений моделей (гипотезы об остатках);
  • оценка качества прогнозов моделей, выбор наилучшей модели;
  • построение прогноза на требуемый период и предсказательного интервала для него;
  • интерпретация полученных результатов в терминах исходной задачи.

Отчёт каждого студента рецензируется назначенным одногруппником. Задачей рецензента является проверка корректности выбора метода решения, полноты его применения и понятности изложения. Вместе с финальной версией отчёта рецензируемый присылает список замечаний рецензента к этой версии, если они имеются. В случае, к работе нет существенных замечаний, отличных от замечаний рецензента, рецензент получает балл. Дальнейшая доработка отчёта происходит без участия рецензента.

Предварительные версии отчётов принимаются до 23:59 14.12, финальные, по результатам работы с рецензентом — до 23:59 21.12.

Посещаемость сервисов Яндекса

Яндекс измеряет месячную аудиторию сервисов, по наиболее старым из них есть статистика за последние 5-6 лет.

Ромов: предсказать месячную аудиторию сервиса "Яндекс.Маркет" на все месяцы 2014 года.
Морозова: предсказать месячную аудиторию сервиса "Мой круг" на все месяцы 2014 года.

Объём стока реки Бойсе

Имеются данные по среднемесячному объёму стока реки Бойсе в районе города Твин Спрингс за каждый месяц с января 1960 по декабрь 2008 года.

Меркулова: предсказать среднемесячный объём стока реки на каждый месяц 2013 года.

Индекс реальных инвестиций в основной капитал

Сотрудниками ГУ-ВШЭ по данным Федеральной службы государственной статистики рассчитан индекс реальных инвестиций в основной капитал, приведённый относительно января 1994 года. Имеются данные на каждый месяц с января 1994 по сентябрь 2013 года.

Березин: построить прогноз для значения индекса на каждый месяц 2014 года.

Число убийств и самоубийств в Австралии

Измерено среднегодовое число убийств и самоубийств на 100000 населения при помощи огнестрельного оружия и с использованием всех остальных средств в Австралии с 1905 по 2004 годы (имеются пропуски).

Огнева: смоделировать среднегодовое число убийств, оценить уровни для 2005-2013 годов.
Нижибицкий: смоделировать долю среднегодового числа самоубийств, совершаемых при помощи огнестрельного оружия, среди всех самоубийств. В 1996-1997 годах в Австралии было изменено законодательство в отношении разрешения на хранение и использование огнестрельного оружия, в ходе программы по разоружению было изъято 600000 единиц оружия (при численности населения в 20000000 человек). Какой эффект это оказало на исследуемый признак?

Средняя номинальная заработная плата в России

На каждый месяц с января 1993 года рассчитан уровень средней номинальной заработной платы в рублях. Среднемесячная номинальная заработная плата исчисляется исходя из фонда заработной платы работников, деленного на среднесписочную численность работников. В фонд заработной платы включаются начисленные суммы в денежной и натуральной формах за отработанное время и выполненную работу, неотработанное, но оплаченное время (например, ежегодные отпуска), стимулирующие доплаты и надбавки, премии и единовременные поощрения, компенсационные выплаты, связанные с режимом работы и условиями труда.

Кондрашкин: построить прогноз для уровня средней номинальной заработной платы на каждый месяц до конца 2014 года.

Число автомобилей, производимых в Великобритании

С первого квартала 1977 по первый квартал 2005 года имеются данные о количестве автомобилей, произведённых в Великобритании, в тысячах штук.

Гавриков: построить прогноз на каждый квартал 2014-2015 года, оценить точность прогноза.

Продажи сувениров

Известны ежемесячные объёмы продаж сувениров в магазине на пляжном курорте в Квинсленде, Австралия. Данные приведены за семь лет, первый месяц — январь, пропусков нет.

Малышева: построить предсказание объёмов продаж на следующие двенадцать месяцев.

Смертность от сердечно-сосудистых заболеваний

Имеются данные по средней дневной смертности от сердечно-сосудистых заболеваний в округе Лос-Анджелес в 1970-1979 годах. Собраны данные по пятисот восьми (идущим подряд) неделям, за каждую из этих недель известна также средняя температура воздуха и мера его загрязнённости.

Лобачёва: считая для последних 50 недель показатель смертности неизвестным, построить его оценку с учётом температуры и загрязнённости воздуха.

Свободные цены на товарном рынке

Конференция ООН по торговле и развитию (ЮНКТАД) собирает ежемесячные данные по свободным ценам на товарном рынке основных продуктов. Имеются данные с января 1960 года по настоящий момент.

Зак: спрогнозировать стоимость алюминия на Лондонской бирже металлов на каждый месяц до конца 2014 года.
Куракин: спрогнозировать стоимость бананов при импорте из Центральной Америки в США на каждый месяц до конца 2014 года.
Любимцева: спрогнозировать стоимость необработанного табака при импорте в США на каждый месяц до конца 2014 года.

Уровень безработицы

Статистическая служба Европейского союза собирает данные по среднемесячному уровню безработицы в тысячах людей с 1983 года.

Фонарев: построить прогноз числа безработных во Франции на каждый месяц 2014 года.
Борисов: построить прогноз числа безработных в Италии на каждый месяц 2014 года.

Смертность в ДТП

Известно число смертей и тяжких телесных повреждений, полученных в результате ДТП в Великобритании за каждый месяц с января 1969 по декабрь 1984.

Остапец: в феврале 1983 был принят закон об обязательном использовании ремней безопасности. Как он повлиял на число серьёзно пострадавших в ДТП в наблюдаемый период? По имеющимся данным оценить его эффект за пять лет с момента принятия.

Длина суток

IERS Earth Orientation Centre располагает данными о среднегодовой длительности суток (она варьируется из-за крупных геологических событий). Для каждого года 1623 по 2005 дано отклонение от идеальной продолжительности суток в миллисекундах.

Потапенко: оценить величину для каждого года с 2006 по 2020.

Счета за электроэнергию

Имеются помесячные данные о тратах на электроэнергию одного фиксированного домохозяйства на среднем западе США. За каждый месяц 1991-2000 годов приведены затраты на электроэнергию в долларах. Для объяснения колебаний размера счёта приведены следующие переменные: среднемесячная температура по данным последних тридцати лет, погодные индексы CDD и HDD (CDD — Cooling Degree Day — количество градусов, на которые средняя дневная температура больше 65°F, взятое суммой за все дни месяца; HDD — Heating Degree Day — аналогично, суммарное количество градусов, на которое средняя дневная температура меньше 65°F), число проживающих в доме членов семьи, индикатор установки нового счётчика, индикаторы установки двух новых тепловых насосов, объём потребления электроэнергии в киловатт-часах.

Ссылки

Источник — «http://poligon.machinelearning.ru/wiki/index.php?title=%D0%A1%D1%82%D0%B0%D1%82%D0%B8%D1%81%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7_%D0%B4%D0%B0%D0%BD%D0%BD%D1%8B%D1%85_%28%D0%BA%D1%83%D1%80%D1%81_%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D0%B9%2C_%D0%9A.%D0%92.%D0%92%D0%BE%D1%80%D0%BE%D0%BD%D1%86%D0%BE%D0%B2%29/2013»