Прогнозирование объемов продаж новых товаров (отчет)
Материал из MachineLearning.
(→Отчет о полученных результатах) |
(→Описание системы) |
||
| (32 промежуточные версии не показаны) | |||
| Строка 71: | Строка 71: | ||
</center> | </center> | ||
| - | Где Quant(<tex>y_{i} | x_{i}</tex>) обозначает условную квантиль <tex>y_{i}</tex> на векторе регрессора <tex>x_{i}</tex>. | + | Где Quant(<tex>y_{i} | x_{i}</tex>) обозначает условную квантиль <tex>y_{i}</tex> на векторе регрессора <tex>x_{i}</tex>. |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| + | Аналог линейной модели для Q-ого квантиля определяется таким же образом. То есть <tex>\hat b</tex> , оценка для b в соотношении (1) — называемом Q-ой квантильной регрессией — решает задачу | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
<center> | <center> | ||
| - | <tex> \min_{b} (\sum_{i:y_{i}>=b}Q|y_{i}-b|+ \sum_{i:y_{i}<b}(1-Q)|y_{i}-b| ) | + | <tex> \min_{b}</tex> (1/n)<tex>(\sum_{i:y_{i}>=x'_{i}b}Q|y_{i}-x'_{i}b|+ \sum_{i:y_{i}<x'_{i}b}(1-Q)|y_{i}-x'_{i}b| )=\min_{b}</tex> (1/n)<tex>\sum_{i=1}^{n}r(u_{i}) (2) </tex> |
</center> | </center> | ||
| - | + | где r(λ)= (Q − I(λ < 0))λ — контрольная функция (check function),a I(.)-обычная индикаторная функция. | |
| - | + | ||
| - | < | + | |
| - | + | ||
| - | |||
| + | Важным частным случаем модели квантильной регрессии является медианная регрессия (Q=1/2) или знаковый статистический метод. Рассмотрим его первым. Знаковый метод исходит из предположения, что случайные ошибки могут быть положительными или отрицательными с равными вероятностями. Следовательно, линия регрессии будет проходить так, чтобы с каждой стороны от нее было равное количество наблюдений. | ||
| + | Q = 0.25. По определению квантили, вероятность того, что ошибки меньше нуля будет равна 25%. Следовательно, линия регрессии будет проходить ниже линии медианной регрессии | ||
| + | |||
| + | x - переменная времени в нашем случае, | ||
| + | |||
| + | <tex>\hat{Y}</tex> = ax+b - предполагаемые значения оценок продаж | ||
| + | |||
| + | Y - реальные значения продаж | ||
| + | |||
| + | Минимизация функционала: | ||
<center> | <center> | ||
| - | <tex> \min_{b} | + | <tex> \min_{(a, b)} (\sum_{\hat{Y} - Y >= 0 }Q|\hat{Y} - Y|+ \sum_{\hat{Y} - Y < 0 }(1-Q)|\hat{Y} - Y| ) </tex> |
</center> | </center> | ||
| - | + | <center> | |
| + | По полученным значениям коэффициентов а и b проводим прямую прогноз. | ||
| - | |||
'''Эвристические алгоритмы''' | '''Эвристические алгоритмы''' | ||
</center> | </center> | ||
| Строка 121: | Строка 116: | ||
<center><tex>y=log(x)</tex></center> | <center><tex>y=log(x)</tex></center> | ||
| - | После прогноза сравнивается его ошибка на последующей неделе у | + | После прогноза сравнивается его ошибка на последующей неделе у базового алгоритма и эвристического. Если ошибка получилось меньше на эвристическом, то для дальнейшего прогноза будет использоваться он, и базовый в противном случае. |
=== Варианты или модификации === | === Варианты или модификации === | ||
| Строка 128: | Строка 123: | ||
== Описание системы == | == Описание системы == | ||
| - | * Описание системы: [http://mlalgorithms.svn.sourceforge.net/ | + | * Описание системы: [http://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Group674/Litvinov2009NewGoods/Docs/Systemdocs.doc] |
| - | * Ссылка на файлы системы: [ | + | * Ссылка на файлы системы: [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Group674/Litvinov2009NewGoods/] |
== Отчет о полученных результатах == | == Отчет о полученных результатах == | ||
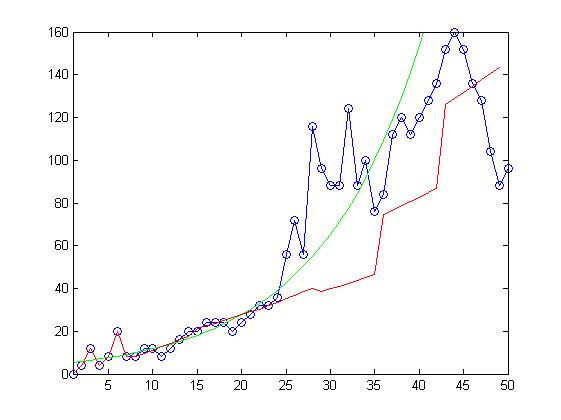
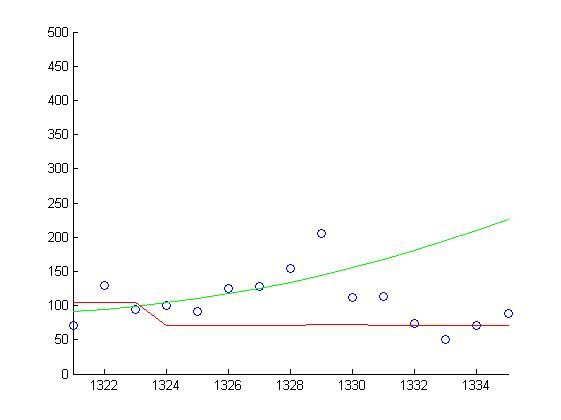
| - | < | + | <center>'''Пример работы квантильной регрессии на модельных данных'''</center> |
| + | |||
| + | [[Изображение:examp1.jpg|800px]] | ||
| + | |||
| + | модельные данные(синяя линия) - случайные величины, распределенные по нормальному закону | ||
| + | чёрная - teta = 0.75, красная teta = 0.25, зелёная - 0.5 | ||
| + | |||
| + | <center>'''Приведём сначала варианты настройки базового алгоритма на различных парметрах'''</center> | ||
Параметр stp подбирался в зависимости от параметра rr (сумма модулей отклонения прогноза от реальных данных за месяц) | Параметр stp подбирался в зависимости от параметра rr (сумма модулей отклонения прогноза от реальных данных за месяц) | ||
| Строка 193: | Строка 195: | ||
[[Изображение:teta5.jpg|650px]] | [[Изображение:teta5.jpg|650px]] | ||
| + | |||
| + | |||
| + | <center>'''Пример работы эвристических алгоритмов'''</center> | ||
| + | |||
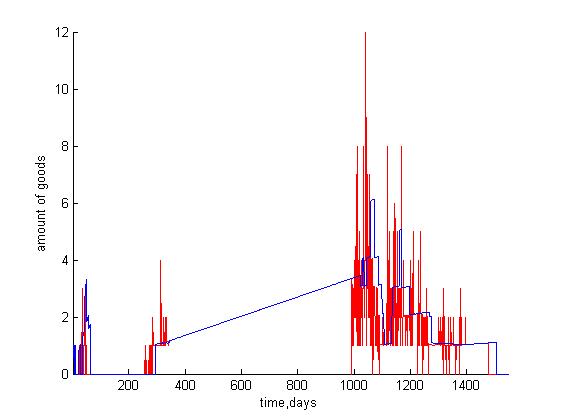
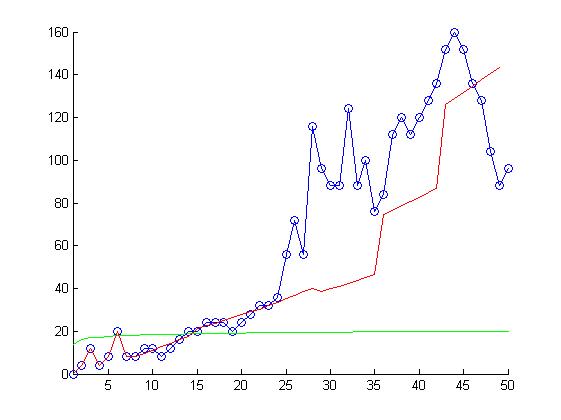
| + | Прогноз, полученный с помощью экспоненты. | ||
| + | |||
| + | Красная линия - базовый алгоритм, зелёная - эвристический. | ||
| + | ошибка базового алгоритма ~600, экспоненты ~400 | ||
| + | |||
| + | |||
| + | |||
| + | [[Изображение:exp2.jpg|650px]] | ||
| + | |||
| + | |||
| + | |||
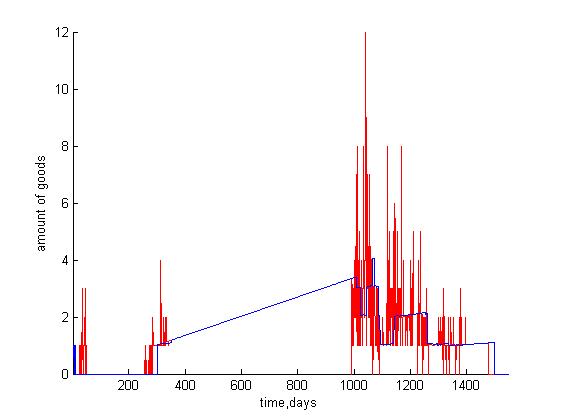
| + | ошибка базового алгоритма ~400, экспоненты ~200 | ||
| + | |||
| + | [[Изображение:exp.jpg|650px]] | ||
| + | |||
| + | Прогноз, полученный с помощью логарифма. | ||
| + | |||
| + | Красная линия - базовый алгоритм, зелёная - эвристический. | ||
| + | ошибка базового алгоритма ~600, логарифмом ~1600 | ||
| + | |||
| + | [[Изображение:log1.jpg|650px]] | ||
| + | |||
| + | ошибка базового алгоритма ~400, логарифмом ~300 | ||
| + | |||
| + | [[Изображение:log.jpg|650px]] | ||
| + | |||
| + | Прогноз, полученный с помощью параболы. | ||
| + | |||
| + | Красная линия - базовый алгоритм, зелёная - эвристический. | ||
| + | ошибка базового алгоритма ~600, параболы ~800 | ||
| + | |||
| + | [[Изображение:parab1.jpg|650px]] | ||
| + | |||
| + | ошибка базового алгоритма ~400, параболы ~700 | ||
| + | |||
| + | [[Изображение:parab.jpg|650px]] | ||
== Список литературы == | == Список литературы == | ||
| Строка 203: | Строка 245: | ||
3)К. В. Воронцов, Лекции по логическим алгоритмам классификации | 3)К. В. Воронцов, Лекции по логическим алгоритмам классификации | ||
| - | {{ | + | {{ЗаданиеВыполнено|Литвинов Игорь|В.В. Стрижов|15 декабря 2009|Litvinov|Strijov}} |
| + | [[Категория:Практика и вычислительные эксперименты]] | ||
__NOTOC__ | __NOTOC__ | ||
Текущая версия
Введение в проект
Описание проекта
Цель проекта
Цель проекта - прогнозирование еженедельных продаж новых товаров.
Обоснование проекта
Результаты проекта могут быть использованы для планирования объёмов продаж новых товаров.
Описание данных
Дано: товарный классификатор (иерархия товарных групп); региональный классификатор (иерархия магазинов и регионов); товародвижения (продажи, поставки, остатки и пр., праздники и промо-акции).
Критерии качества
Продажи прогнозируется по каждому товару раздельно. Прогнозирование объёмов продаж на неделю основывается на предыстории продаж за фиксированное число дней. Это число дней регулируется переменной stp (количество шагов - количество дней, на которых основывается прогноз) в базовом алгоритме(квантильная регрессия). Критерием качества служит сумма модулей отклонения прогноза от реальной величины покупок по дням.
Требования к проекту
Сумма модулей отклонения в базовом алгоритме проекта должна быль меньше, чем для скользящего среднего за 30 дней. Эвристические алгоритмы будут применяться в прогнозировании, если только ошибка на них будет меньше, чем ошибка на базовом алгоритме за 1 неделю.
Выполнимость проекта
Прогнозирование объёмов продаж новых товаров производится в будние дни (время праздников и промо-акций в проекте не рассматривается).
Используемые методы
Базовый алгоритм
Прогнозирование производится методом квантильной регрессии для различных квантилей Θ (0.25; 0.4; 0.5; 0.6; 0.75). При прогнозировании можно менять параметр stp.
Также используются эвристические алгоритмы прогнозирование продаж экспонентой, параболой и логарифмом.
Постановка задачи
На основе данных продаж за фиксированное число дней (параметр stp) прогнозируются продажи новых товаров на 7 дней вперёд с наибольшей вероятностью (Θ=0.5) и вероятностями 25%, 40%. Будем использовать функционал качества
где y, соответственно известное значение и прогноз.
- временной ряд для каждого из товаров,
- значение продаж для каждого такого ряда.
Описание алгоритмов
В проекте использовался метод квантильной регрессии и эвристические алгоритмы.
Обзор литературы
Для прогнозирования объёмов продаж новых товаров в литературе описываются различные методы. Метод квантильной регрессии впервые применён в [1], прогнозирование с помощью которого наиболее точно и позволяет прогнозировать c разными вероятностями [2]. Квантильная регрессия с параметром 0.5 является линейной, которая рассматриватся в [3].
Базовые предположения
Предполагается, что наилучший прогноз будет получен с помощью квантильной регрессии с параметром Θ=0.5. Прогноз требуется не более чем на 7 дней.
Математическое описание
Общая модель квантильной регрессии
Пусть , i=1,...,n - некоторые переменные, где
- K×1 вектор независимых переменных в уравнении регрессии. Допускается, что
≤τ |
)=
(τ-
b|
), i=1,...,n.
Это соотношение — в другой формулировке — может быть переписано как
,
(1)
Где Quant() обозначает условную квантиль
на векторе регрессора
.
Аналог линейной модели для Q-ого квантиля определяется таким же образом. То есть , оценка для b в соотношении (1) — называемом Q-ой квантильной регрессией — решает задачу
(1/n)
(1/n)
где r(λ)= (Q − I(λ < 0))λ — контрольная функция (check function),a I(.)-обычная индикаторная функция.
Важным частным случаем модели квантильной регрессии является медианная регрессия (Q=1/2) или знаковый статистический метод. Рассмотрим его первым. Знаковый метод исходит из предположения, что случайные ошибки могут быть положительными или отрицательными с равными вероятностями. Следовательно, линия регрессии будет проходить так, чтобы с каждой стороны от нее было равное количество наблюдений.
Q = 0.25. По определению квантили, вероятность того, что ошибки меньше нуля будет равна 25%. Следовательно, линия регрессии будет проходить ниже линии медианной регрессии
x - переменная времени в нашем случае,
= ax+b - предполагаемые значения оценок продаж
Y - реальные значения продаж
Минимизация функционала:
По полученным значениям коэффициентов а и b проводим прямую прогноз.
Эвристические алгоритмы
Будем полагать, что товар новый в течении 5 недель. По 1 неделе(7 точкам) будем прогнозировать продажи на последующее время, предполагая, что продажи новых товаров будут расти по экспоненте
параболе
или логарифму
После прогноза сравнивается его ошибка на последующей неделе у базового алгоритма и эвристического. Если ошибка получилось меньше на эвристическом, то для дальнейшего прогноза будет использоваться он, и базовый в противном случае.
Варианты или модификации
Варианты алгоритма зависят от параметров stp и Q. Значения параметров выбираются по результатам экспериментов. В качестве функций для прогнозирования объёмов продаж новых товаров могут использоваться любые растущие функции(в проекте рассматривались только экспонента, логарифм,квадратная парабола)
Описание системы
Отчет о полученных результатах
модельные данные(синяя линия) - случайные величины, распределенные по нормальному закону чёрная - teta = 0.75, красная teta = 0.25, зелёная - 0.5
Параметр stp подбирался в зависимости от параметра rr (сумма модулей отклонения прогноза от реальных данных за месяц)
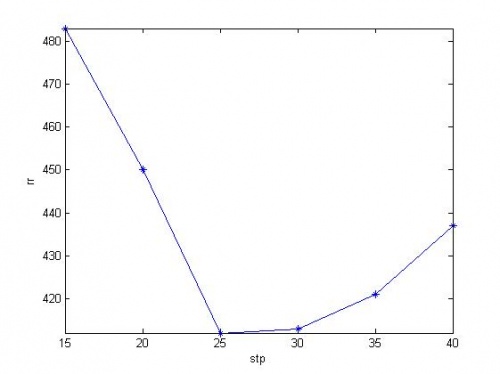
Для наименьшего rr выбирается значение stp= 25, которое используется в дальнейшем для расчётов в качестве оптимального.
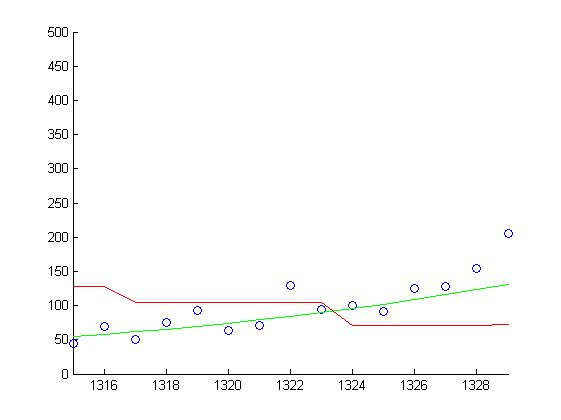
Проанализируем зависимость ошибок алгоритма для разного параметра квантильной регрессии teta. Прогнозирование ведётся по одному товару, в качестве примера рассмотрен товар с индексом 1 в таблице данных.
1) Параметр teta=0.5,
stp = 25
Значения ошибок rs =418.4907 rr =412.4245
где rs - сумма модулей отклонения средней за месяц величины от реальных данных

2) Параметр teta=0.25,
stp = 25
Значения ошибок rs =418.4907 rr =532.9533
3) Параметр teta=0.75,
stp = 25
Значения ошибок rs =418.4907 rr =391.8512
4) Параметр teta=0.6,
stp = 25
Значения ошибок rs =418.4907 rr =382.4836
5) Параметр teta=0.4,
stp = 25
Значения ошибок rs =418.4907 rr =457.0586
Прогноз, полученный с помощью экспоненты.
Красная линия - базовый алгоритм, зелёная - эвристический. ошибка базового алгоритма ~600, экспоненты ~400
ошибка базового алгоритма ~400, экспоненты ~200
Прогноз, полученный с помощью логарифма.
Красная линия - базовый алгоритм, зелёная - эвристический. ошибка базового алгоритма ~600, логарифмом ~1600
ошибка базового алгоритма ~400, логарифмом ~300
Прогноз, полученный с помощью параболы.
Красная линия - базовый алгоритм, зелёная - эвристический. ошибка базового алгоритма ~600, параболы ~800
ошибка базового алгоритма ~400, параболы ~700
Список литературы
1) Koenker and G. Bassett, Jr. "Regression Quantiles," Econometrica, Vol.46 No1 (January, 1978)
2)Постникова Е. (2000) Квантильная регрессия. НГУ.
3)К. В. Воронцов, Лекции по логическим алгоритмам классификации
| | Данная статья была создана в рамках учебного задания.
См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |