Метод k взвешенных ближайших соседей (пример)
Материал из MachineLearning.
(→Смотри также) |
(→Исходный код) |
||
| (22 промежуточные версии не показаны) | |||
| Строка 28: | Строка 28: | ||
=== Алгоритм отыскания оптимальных параметров === | === Алгоритм отыскания оптимальных параметров === | ||
Оптимальные значения параметров <tex>K</tex> и <tex>q</tex> определяют по критерию скользящего контроля с исключением объектов по одному: | Оптимальные значения параметров <tex>K</tex> и <tex>q</tex> определяют по критерию скользящего контроля с исключением объектов по одному: | ||
| - | <tex>(k^{*};q^{*}) = \arg{ } \ | + | <tex>(k^{*};q^{*}) = \arg{ } \min_{k,q}\ LOO(k;q;X^\ell\),</tex> где |
| - | <tex>LOO(k;q;X^\ell\)= \sum_{i=1}^l\[y_i = a(x_i;X^l/x_i;k;q)]. </tex> | + | <tex>LOO(k;q;X^\ell\)= \sum_{i=1}^l\[y_i = a(x_i;X^l/x_i;k;q)] </tex> в случае равной значимости ошибок и <tex>LOO(k;q;X^\ell\)= \sum_{i=1}^l err(y_i, a(x_i;X^l/x_i;k;q)) </tex>, если ошибки не равнозначны. Здесь <tex>err(i,j)</tex> - матрица, <tex>(i,j)</tex> элементом которой является величина ошибки при классификации объекта <tex>i</tex>ого класса как объект <tex>j</tex>ого класса. |
| + | === Алгоритм отбора признаков === | ||
| + | Если признаков слишком много, а расстояние вычисляется как сумма отклонений по отдельным признакам, то возникает проблема проклятия размерности. Суммы большого числа отклонений с большой вероятностью имеют очень близкие значения (согласно закону больших чисел). Получается, что в пространстве высокой размерности все объекты примерно одинаково далеки друг от друга; выбор k ближайших соседей становится практически произвольным. | ||
| + | |||
| + | Проблема решается путём отбора относительно небольшого числа информативных признаков (features selection). | ||
| + | |||
| + | В работе использован алгоритм жадного добавления признаков Add. | ||
| + | |||
| + | В алгоритме Add строится набор информативных призаков. Работа начинается с пустого множества. На каждом шаге <tex>i</tex> добавяется новый признак, который при использовании с ранее выбранными минимизирует внешний критерий при числе признаков равном <tex>i</tex> (в данной работе внешний критерий - это <tex>LOO(k;q;X^\ell\)</tex> ). Если в течении <tex>d</tex> шагов значение внешнего критерия не | ||
| + | доставляло минимум внешнему критерию или добавлены все признаки, то алгоритм прекращает работу. | ||
== Некоторые достоинства и недостатки алгоритма <tex>K</tex> взвешенных ближайших соседей как метрического алгоритма == | == Некоторые достоинства и недостатки алгоритма <tex>K</tex> взвешенных ближайших соседей как метрического алгоритма == | ||
| Строка 150: | Строка 159: | ||
На графике по осям отложены величины признаков объектов, различные классы показаны крестиками различных цветов, а результат классификации показан кружочками соотвествующих цветов. Алгоритм допустил 10% ошибок при обучении и 9% ошибок на контрольной выборке. | На графике по осям отложены величины признаков объектов, различные классы показаны крестиками различных цветов, а результат классификации показан кружочками соотвествующих цветов. Алгоритм допустил 10% ошибок при обучении и 9% ошибок на контрольной выборке. | ||
| - | === Пример на реальных данных: ирисы === | + | === Пример на реальных данных 1: ирисы === |
| - | Проведем проверку алгоритма на классической задаче: [http://archive.ics.uci.edu/ml/datasets/Iris Ирисы Фишера] | + | Проведем проверку алгоритма на классической задаче: [http://archive.ics.uci.edu/ml/datasets/Iris Ирисы Фишера]. |
Объектами являются три типа ирисов: [http://ru.wikipedia.org/wiki/%D0%98%D1%80%D0%B8%D1%81_%D1%89%D0%B5%D1%82%D0%B8%D0%BD%D0%B8%D1%81%D1%82%D1%8B%D0%B9 setosa], [http://en.wikipedia.org/wiki/Iris_versicolor versicolor], virginica | Объектами являются три типа ирисов: [http://ru.wikipedia.org/wiki/%D0%98%D1%80%D0%B8%D1%81_%D1%89%D0%B5%D1%82%D0%B8%D0%BD%D0%B8%D1%81%D1%82%D1%8B%D0%B9 setosa], [http://en.wikipedia.org/wiki/Iris_versicolor versicolor], virginica | ||
| Строка 191: | Строка 200: | ||
Z =FeaturesStand(Z); | Z =FeaturesStand(Z); | ||
XL = Z(1:n, :); | XL = Z(1:n, :); | ||
| - | + | Xtemp = Z(n+1:n+p, :); | |
%% choosing parametrs | %% choosing parametrs | ||
PP = ParAdjust(XL, YL); | PP = ParAdjust(XL, YL); | ||
| Строка 197: | Строка 206: | ||
PP.YL = YL; | PP.YL = YL; | ||
%% classification | %% classification | ||
| - | Y = WeightKNN( | + | Y = WeightKNN(Xtemp, PP); |
%% plotting resulting classification | %% plotting resulting classification | ||
| Строка 214: | Строка 223: | ||
На графике различные классы показаны крестиками различных цветов, а результат классификации показан кружочками соотвествующих цветов. Алгоритм хорошо классифицировал ирисы, допустив 4% ошибок. | На графике различные классы показаны крестиками различных цветов, а результат классификации показан кружочками соотвествующих цветов. Алгоритм хорошо классифицировал ирисы, допустив 4% ошибок. | ||
| - | == | + | === Пример на реальных данных 2: данные по кредитованию одним из немецких банков === |
| - | + | Проведем проверку алгоритма на задаче из репозитория UCI: [http://archive.ics.uci.edu/ml/datasets/Statlog+%28German+Credit+Data%29 Statlog (German Credit Data) Data Set ]. Объектами являются анкеты людей, желавших получить кредит в банке. Изначально анкеты содержали 20 пунктов, таких как состояние банковсого счета заемщика, информация о его кредитной истории, цель займа, величина займа, возраст заемщика, время с момента трудоустройства на текущее место работы и другие. Но так как некоторые из них не были числовыми, а многие алгоритмы (в том числе рассматриваемый в данной статье) работают только с числовыми признаками, то из 20 разнородных признаков было составлено 24 числовых. Ответы - «хорошим» или «плохим» заемщиком оказался человек, получивший кредит. | |
| + | По условию задачи, распознать «плохого» заемщика как «хорошего» в 5 раз хуже, чем «хорошего» как «плохого». | ||
| + | При обучении использован алгоритм отбора признаков Add. | ||
| + | В выборке представлена 1000 объектов. В качестве обучающей выборки выбраны первые 690 объектов, в качестве контроля 310 оставшихся. | ||
| + | <source lang="matlab"> | ||
| + | %% Example 'german credits' | ||
| + | % Example with real data | ||
| + | %% data preparation | ||
| + | %% load data | ||
| + | load 'germanDataNumeric.txt'; | ||
| + | S = germanDataNumeric; | ||
| + | PP.XL = S(1:690,1:24); | ||
| + | % if votes are equal, it is better to classify as 2nd class. Make new marks | ||
| + | %of classes | ||
| + | PP.YL = 3-S(1:690,25); | ||
| + | % and change cost matrix | ||
| + | PP.errCost = [0 5; 1 0]; | ||
| + | % initialization of d parametr | ||
| + | PP.d = 24; | ||
| + | %% run add algorithm | ||
| + | [features, jBest] = Add(PP); | ||
| + | %% run ParAdjust with selected features | ||
| + | % initialization of PP, X | ||
| + | PP = []; | ||
| + | PP.XL = zeros(690,jBest); | ||
| + | PP.XL= S(1:690,features(1:jBest)); | ||
| + | X= S(691:1000,features(1:jBest)); | ||
| + | PP.YL = 3-S(1:690,25); | ||
| + | PP.errCost = [0 5; 1 0]; | ||
| + | % run FeaturesStand | ||
| + | [p, m] = size(X); | ||
| + | [n, m] = size(PP.XL); | ||
| + | Z = [PP.XL; X]; | ||
| + | Z =FeaturesStand(Z); | ||
| + | PP.XL = Z(1:n, :); | ||
| + | X = Z(n+1:n+p, :); | ||
| + | % run ParAdjust | ||
| + | PP = ParAdjustMod(PP.XL, PP.YL, PP) | ||
| + | %% run WeightKNN | ||
| + | Y = WeightKNN(X, PP); | ||
| + | YTrue = 3- S(691:1000,25); | ||
| + | %% count weighted errors and errors | ||
| + | ErrW =0; | ||
| + | for i = [1:310] | ||
| + | ErrW = ErrW+ PP.errCost(YTrue(i), Y(i)); | ||
| + | end | ||
| + | Err = sum(Y~=YTrue); | ||
| + | </source> | ||
| + | |||
| + | [[Изображение:WKNN_German.png|500px]] | ||
| + | |||
| + | На графике построена зависимость величины взвешенных ошибок при обучении от числа используемых признаков. | ||
| + | Алгоритмом Add было отобрано 5 признаков(номера 1, 15, 14, 3, 19). Названия признаков: 1 - текущее состояние банковского счета, 15 - жилье (собственное, снимаете или бесплатно предоставляется), 14 - other installment plans (bank, stores or none), 3 - сведения о ранее выдававшихся кредитах и 19 - один из девяти признаков, полученных в резульате обаботки семи пунктов анкеты (пп 4, 8, 10, 15, 17). | ||
| + | |||
| + | Средней ценой ошибки назовем величину <tex> AE= (\sum_{i=1}^m err(y_i, a(x_i)) )/m </tex>, где, как и ранее, <tex>err(i,j)</tex> - матрица, <tex>(i,j)</tex> элементом которой является величина ошибки при классификации объекта <tex>i</tex>ого класса как объект <tex>j</tex>ого класса. | ||
| + | |||
| + | При обучении средняя цена ошибок алгоритма составила 0.52 и 0.83 на контроле. Так как алгоритм допустил значительно больше ошибок на обучении, чем на контроле, то уместно говорить о [[переобучение|переобучении]]. | ||
| + | |||
| + | Отметим также то, что средняя цена ошибок алгоритма k взвешенных ближайших соседей, запущенный без отбора признаков, составила 0.77 при обучении и 0.68 на контроле. | ||
| + | |||
| + | Таким образом, алгоритм отбора признаков существенно снизил число с 24 до 5, понизив качество классификации. | ||
| + | |||
| + | Приведем результаты работы разных алгоритмов на данной выборке: | ||
| + | {| class="wikitable" style="text-align: center;" | ||
| + | |- bgcolor="#cccccc" | ||
| + | ! width=20 % |Название алгоритма | ||
| + | ! width=15 % |Стоимость ошибкок при обучении | ||
| + | ! width=15 % |Стоимость ошибкок на контроле | ||
| + | |||
| + | |- | ||
| + | | Discrim || 0.509 || 0.535 | ||
| + | |- | ||
| + | | Quadisc || 0.431 || 0.619 | ||
| + | |- | ||
| + | | Logdisc || 0.499 || 0.538 | ||
| + | |- | ||
| + | | SMART || 0.389 || 0.601 | ||
| + | |- | ||
| + | | ALLOC80 || 0.597 || 0.584 | ||
| + | |- | ||
| + | | k-NN || 0.000 ||0.694 | ||
| + | |- | ||
| + | |k-NN,k=17, eucl,std || - || 0.411 | ||
| + | |- | ||
| + | | CASTLE || 0.582 || 0.583 | ||
| + | |- | ||
| + | | CART || 0.581 || 0.613 | ||
| + | |- | ||
| + | | IndCART || 0.069 || 0.761 | ||
| + | |- | ||
| + | | NewID || 0.000 || 0.925 | ||
| + | |- | ||
| + | | AC2 || 0.000 || 0.878 | ||
| + | |- | ||
| + | | Baytree || 0.126 || 0.778 | ||
| + | |- | ||
| + | | NaiveBay || 0.600 ||0.703 | ||
| + | |- | ||
| + | | CN2 || 0.000 ||0.856 | ||
| + | |- | ||
| + | | C4.5 || 0.640 || 0.985 | ||
| + | |- | ||
| + | | ITrule || * || 0.879 | ||
| + | |- | ||
| + | | Cal5 || 0.600 || 0.603 | ||
| + | |- | ||
| + | | Kohonen || 0.689 || 1.160 | ||
| + | |- | ||
| + | | DIPOL92 || 0.574 ||0.599 | ||
| + | |- | ||
| + | | Backprop || 0.446 || 0.772 | ||
| + | |- | ||
| + | | RBF || 0.848 || 0.971 | ||
| + | |- | ||
| + | | LVQ || 0.229 || 0.963 | ||
| + | |- | ||
| + | | WKNN, std || 0.770 || 0.732 | ||
| + | |- | ||
| + | | WKNN, std, Add || 0.516 || 0.839 | ||
| + | |- | ||
| + | |} | ||
| + | Последние две строки таблицы - результат работы алгоритма, рассматриваемого в данной статье( WKNN, std - без отбора признаков, WKNN, std, Add - с отбором). Данные для построения таблицы взяты с http://www.is.umk.pl/projects/datasets-stat.html . | ||
| + | |||
| + | == Исходный код == | ||
| + | Скачать листинги алгоритмов можно здесь | ||
| + | [http://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Group674/Yanovich2009WeightedKNN/]. | ||
== Смотри также == | == Смотри также == | ||
| Строка 222: | Строка 356: | ||
* [[Метрический классификатор]] | * [[Метрический классификатор]] | ||
* [[Метод ближайших соседей]] | * [[Метод ближайших соседей]] | ||
| + | * [[Переобучение]] | ||
* [[Скользящий контроль]] | * [[Скользящий контроль]] | ||
* [[Численные методы обучения по прецедентам (практика, В.В. Стрижов)]] | * [[Численные методы обучения по прецедентам (практика, В.В. Стрижов)]] | ||
| Строка 228: | Строка 363: | ||
* К. В. Воронцов, Лекции по метрическим алгоритмам классификации | * К. В. Воронцов, Лекции по метрическим алгоритмам классификации | ||
* Bishop C. - Pattern Recognition and Machine Learning (Springer, 2006) | * Bishop C. - Pattern Recognition and Machine Learning (Springer, 2006) | ||
| + | * [http://www.inference.phy.cam.ac.uk/mackay/itila/ The on-line textbook: Information Theory, Inference, and Learning Algorithms], by [[David J.C. MacKay]]. | ||
| + | * Abidin, T. and Perrizo, W. SMART-TV: A Fast and Scalable Nearest Neighbor Based Classifier for Data Mining. Proceedings of ACM SAC-06, Dijon, France, April 23-27, 2006. ACM Press, New York, NY, pp.536-540 | ||
| + | * Wang, H. and Bell, D. Extended k-Nearest Neighbours Based on Evidence Theory. The Computer Journal, Vol. 47 (6) Nov. 2004, pp. 662-672. | ||
| + | * Yu, K. and Ji, L. Karyotyping of Comparative Genomic Hybridization Human Metaphases Using Kernel Nearest-Neighbor Algorithm, Cytometry 2002. | ||
| + | * UCI Machine Learning Repository, available on line at the University of California,Irvine http://www.ics.uci.edu/~mlearn/MLSum mary.html | ||
| - | {{ | + | {{ЗаданиеВыполнено|Янович Юрий|В.В. Стрижов|28 мая 2009|Yanovich|Strijov}} |
| - | + | [[Категория:Метрические алгоритмы классификации]] | |
| + | [[Категория:Практика и вычислительные эксперименты]] | ||
Текущая версия
|
взвешенных ближайших соседей - это метрический алгоритм классификации, основанный на оценивании сходства объектов. Классифицируемый объект относится к тому классу, которому принадлежат ближайшие к нему объекты обучающей выборки.
Постановка задачи
Пусть - множество объектов;
- множество допустимых ответов. Задана обучающая выборка
. Задано множество объектов
.
Требуется найти множество ответов для объектов
.
Алгоритм  взвешенных ближайших соседей
взвешенных ближайших соседей
На множестве объектов задается евклидова функция расстояния
Для произвольного объекта расположим
объекты обучающей выборки
в порядке возрастания расстояний до
:
где через обозначается
тот объект обучающей выборки, который является
-м соседом объекта
.
Аналогичное обозначение введём и для ответа на
-м соседе:
.
Таким образом, произвольный объект порождает свою перенумерацию выборки.
В наиболее общем виде алгоритм ближайших соседей есть
где — заданная весовая функция,
которая оценивает степень важности
-го соседа для классификации объекта
. Так, при
при
алгоритм соответствует медоду
ближайших соседей.
Но в задаче с несколькими возможными ответами максимальная сумма голосов может достигаться на нескольких классах одновременно.
Неоднозначность можно устранить, если в качестве весовой функции взять нелинейную последовательность, например геометрическую прогрессию: в рассматриваемом примере
что соответствует методу
экспоненциально взвешенных ближайших соседей, причем предполагается
.
Алгоритм отыскания оптимальных параметров
Оптимальные значения параметров и
определяют по критерию скользящего контроля с исключением объектов по одному:
где
в случае равной значимости ошибок и
, если ошибки не равнозначны. Здесь
- матрица,
элементом которой является величина ошибки при классификации объекта
ого класса как объект
ого класса.
Алгоритм отбора признаков
Если признаков слишком много, а расстояние вычисляется как сумма отклонений по отдельным признакам, то возникает проблема проклятия размерности. Суммы большого числа отклонений с большой вероятностью имеют очень близкие значения (согласно закону больших чисел). Получается, что в пространстве высокой размерности все объекты примерно одинаково далеки друг от друга; выбор k ближайших соседей становится практически произвольным.
Проблема решается путём отбора относительно небольшого числа информативных признаков (features selection).
В работе использован алгоритм жадного добавления признаков Add.
В алгоритме Add строится набор информативных призаков. Работа начинается с пустого множества. На каждом шаге добавяется новый признак, который при использовании с ранее выбранными минимизирует внешний критерий при числе признаков равном
(в данной работе внешний критерий - это
). Если в течении
шагов значение внешнего критерия не
доставляло минимум внешнему критерию или добавлены все признаки, то алгоритм прекращает работу.
Некоторые достоинства и недостатки алгоритма  взвешенных ближайших соседей как метрического алгоритма
взвешенных ближайших соседей как метрического алгоритма
Достоинства
- Простота реализации.
- Классификацию, проведенную данным алгоритмом, легко интерпретировать путём предъявления пользователю нескольких ближайших объектов.
Недостатки
- Неэффективный расходу памяти и чрезмерное усложнение решающего правила вследствии необходимости хранения обучающей выборки целиком.
- Поиск ближайшего соседа предполагает сравнение классифицируемого объекта со всеми объектами выборки, что требует линейного по длине выборки числа операций.
Вычислительный эксперимент
Показана работа алгоритма в серии задач, основанных как на реальных, так и на модельных данных.
Пример 1
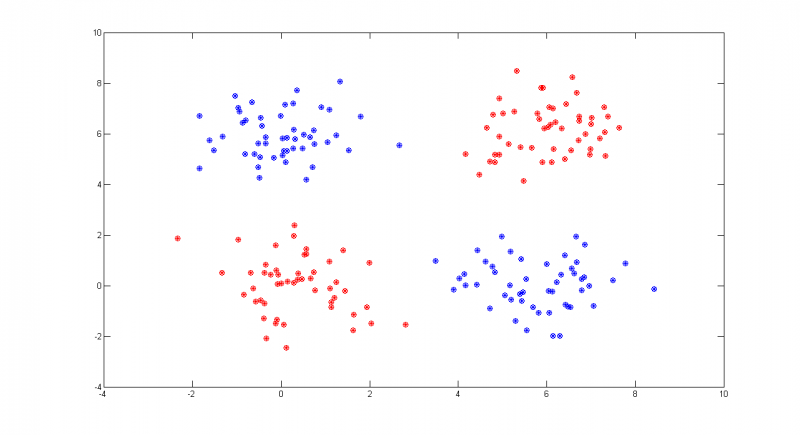
Рассмотрим пример на модельных данных. Выборка состоит из четырех классов, которые являются гауссовскими рапределением с диагональными матрицами ковариации. Классы легко разделимы.
%% Example 1 % Example, which is simply classifed by WeightedKNN. It seems like XOR % problem. %% generate training sample % generate 2 groups of normal classes. Each group consistes of 2 simple % normal classes XL1 = [GetNormClass(50,[0,0],[1,1]); GetNormClass(50,[6,6],[1,1])]; XL2 = [GetNormClass(50,[6,0],[1,1]); GetNormClass(50,[0,6],[1,1])]; XL = [XL1; XL2]; YL = [repmat(1,100,1);repmat(2,100,1)]; %% generate control data with the same distribution X1 = [GetNormClass(50,[0,0],[1,1]); GetNormClass(50,[6,6],[1,1])]; X2 = [GetNormClass(50,[6,0],[1,1]); GetNormClass(50,[0,6],[1,1])]; X = [X1; X2]; Y = [repmat(1,100,1);repmat(2,100,1)]; %% get classification %% choosing parametrs PP = ParAdjust(XL, YL); PP.XL = XL; PP.YL = YL; %% classification Y = WeightKNN(X, PP); %% results visuaisation %% plotting real classes of objects plot(X1(:,1),X1(:,2),'*r'); hold on plot(X2(:,1),X2(:,2),'*b'); %% plotting classification results plot(X(Y == 1,1),X(Y == 1,2),'or'); plot(X(Y == 2,1),X(Y == 2,2),'ob'); hold off
На графике по осям отложены величины признаков объектов, различные классы показаны крестиками различных цветов, а результат классификации показан кружочками соотвествующих цветов. Алгоритм не допустил при классификации ни одной ошибки.
Пример 2
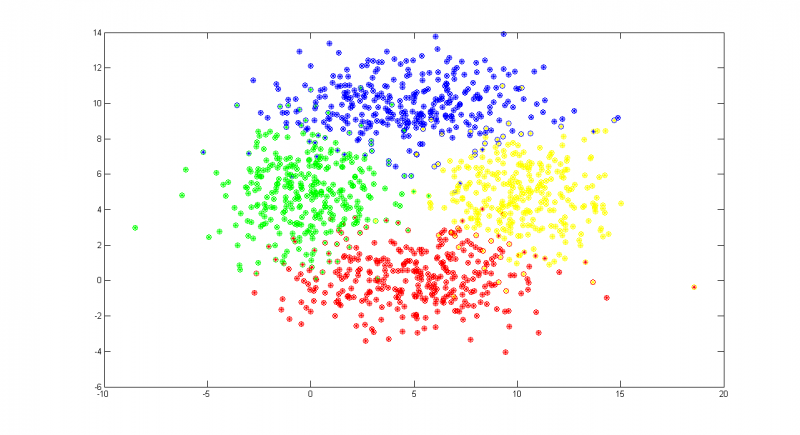
В качестве второго примера возьмем четыре плохо разделимых класса. Классы обладают большой дисперсией. Можно наблюдать области, в которых элементы различны классов проникают в чужие классы.
%% Example 2 % Classes cross each other in this example. Algorithm makes misstakes in % classification. %% generate training sample % generating 4 sample normal classes XL1 = GetNormClass(100,[5,0],[10,2]); XL2 = GetNormClass(100,[5,10],[10,2]); XL3 = GetNormClass(100,[0,5],[4,4]); XL4 = GetNormClass(100,[10,5],[4,4]); XL = [XL1; XL2; XL3; XL4]; YL = [repmat(1,100,1);repmat(2,100,1);repmat(3,100,1);repmat(4,100,1)]; %% generate control data with the same distribution X1 = GetNormClass(100,[5,0],[10,2]); X2 = GetNormClass(100,[5,10],[10,2]); X3 = GetNormClass(100,[0,5],[4,4]); X4 = GetNormClass(100,[10,5],[4,4]); X = [X1; X2; X3; X4]; % X is going to be changed in getting classification. X0 is needed to plot data. X0 = X; %% getting classification %% features standardization [p, m] = size(X); [n, m] = size(XL); Z = [XL; X]; Z =FeaturesStand(Z); XL = Z(1:n, :); X = Z(n+1:n+p, :); %% choosing parametrs PP = ParAdjust(XL, YL); PP.XL = XL; PP.YL = YL; %% classification Y = WeightKNN(X, PP); %% results visuaisation %% plotting real classes of objects plot(X1(:,1),X1(:,2),'*r'); hold on plot(X2(:,1),X2(:,2),'*b'); plot(X3(:,1),X3(:,2),'*g'); plot(X4(:,1),X4(:,2),'*y'); %% plotting classification results plot(X0(Y == 1,1),X0(Y == 1,2),'or'); plot(X0(Y == 2,1),X0(Y == 2,2),'ob'); plot(X0(Y == 3,1),X0(Y == 3,2),'og'); plot(X0(Y == 4,1),X0(Y == 4,2),'oy'); %% count errors errors = sum([Y(1:100) == 1; Y(101:200) == 2; Y(201:300) == 3; Y(301:400) == 4]) hold off
На графике по осям отложены величины признаков объектов, различные классы показаны крестиками различных цветов, а результат классификации показан кружочками соотвествующих цветов. Алгоритм допустил 10% ошибок при обучении и 9% ошибок на контрольной выборке.
Пример на реальных данных 1: ирисы
Проведем проверку алгоритма на классической задаче: Ирисы Фишера. Объектами являются три типа ирисов: setosa, versicolor, virginica
У каждого объекта есть четыре признака: длина лепестка, ширина лепестка, длина чашелистика, ширина чашелистика. Для удобства визуализации результатов будем использовать первые два признака. В качестве обучающей и контрольной выборок выбрано по 25 представителей каждого из типов ирисов.
%% Example 'iris' % Example with real data %% data preparation %% load data load 'iris.txt'; S = iris; %% eliminating first two attributes S(:,1:2) = []; %% divide data into training part and pert to classify XL = S([1:25,51:75,101:125],:); X = S([26:50,76:100,126:150],:); %% creating class labels YL = [ones([25,1]);2*ones([25,1]);3*ones([25,1])]; Y = [ones([25,1]);2*ones([25,1]);3*ones([25,1])]; %% plotting real classes of objects plot(X(Y == 1,1),X(Y == 1,2),'*r'); hold on plot(X(Y == 2,1),X(Y == 2,2),'*b'); plot(X(Y == 3,1),X(Y == 3,2),'*g'); %% getting classification %% features standardization [p, m] = size(X); [n, m] = size(XL); Z = [XL; X]; Z =FeaturesStand(Z); XL = Z(1:n, :); Xtemp = Z(n+1:n+p, :); %% choosing parametrs PP = ParAdjust(XL, YL); PP.XL = XL; PP.YL = YL; %% classification Y = WeightKNN(Xtemp, PP); %% plotting resulting classification plot(X(Y == 1,1),X(Y == 1,2),'or'); plot(X(Y == 2,1),X(Y == 2,2),'ob'); plot(X(Y == 3,1),X(Y == 3,2),'og'); title('Irises classification') xlabel('petal width, cm'); ylabel('petal length, cm'); legend('Iris Setosa','Iris Versicolour','Iris Virginica','Location','NorthWest'); hold off;
На графике различные классы показаны крестиками различных цветов, а результат классификации показан кружочками соотвествующих цветов. Алгоритм хорошо классифицировал ирисы, допустив 4% ошибок.
Пример на реальных данных 2: данные по кредитованию одним из немецких банков
Проведем проверку алгоритма на задаче из репозитория UCI: Statlog (German Credit Data) Data Set . Объектами являются анкеты людей, желавших получить кредит в банке. Изначально анкеты содержали 20 пунктов, таких как состояние банковсого счета заемщика, информация о его кредитной истории, цель займа, величина займа, возраст заемщика, время с момента трудоустройства на текущее место работы и другие. Но так как некоторые из них не были числовыми, а многие алгоритмы (в том числе рассматриваемый в данной статье) работают только с числовыми признаками, то из 20 разнородных признаков было составлено 24 числовых. Ответы - «хорошим» или «плохим» заемщиком оказался человек, получивший кредит. По условию задачи, распознать «плохого» заемщика как «хорошего» в 5 раз хуже, чем «хорошего» как «плохого». При обучении использован алгоритм отбора признаков Add. В выборке представлена 1000 объектов. В качестве обучающей выборки выбраны первые 690 объектов, в качестве контроля 310 оставшихся.
%% Example 'german credits' % Example with real data %% data preparation %% load data load 'germanDataNumeric.txt'; S = germanDataNumeric; PP.XL = S(1:690,1:24); % if votes are equal, it is better to classify as 2nd class. Make new marks %of classes PP.YL = 3-S(1:690,25); % and change cost matrix PP.errCost = [0 5; 1 0]; % initialization of d parametr PP.d = 24; %% run add algorithm [features, jBest] = Add(PP); %% run ParAdjust with selected features % initialization of PP, X PP = []; PP.XL = zeros(690,jBest); PP.XL= S(1:690,features(1:jBest)); X= S(691:1000,features(1:jBest)); PP.YL = 3-S(1:690,25); PP.errCost = [0 5; 1 0]; % run FeaturesStand [p, m] = size(X); [n, m] = size(PP.XL); Z = [PP.XL; X]; Z =FeaturesStand(Z); PP.XL = Z(1:n, :); X = Z(n+1:n+p, :); % run ParAdjust PP = ParAdjustMod(PP.XL, PP.YL, PP) %% run WeightKNN Y = WeightKNN(X, PP); YTrue = 3- S(691:1000,25); %% count weighted errors and errors ErrW =0; for i = [1:310] ErrW = ErrW+ PP.errCost(YTrue(i), Y(i)); end Err = sum(Y~=YTrue);
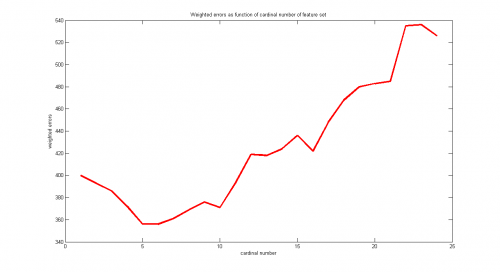
На графике построена зависимость величины взвешенных ошибок при обучении от числа используемых признаков. Алгоритмом Add было отобрано 5 признаков(номера 1, 15, 14, 3, 19). Названия признаков: 1 - текущее состояние банковского счета, 15 - жилье (собственное, снимаете или бесплатно предоставляется), 14 - other installment plans (bank, stores or none), 3 - сведения о ранее выдававшихся кредитах и 19 - один из девяти признаков, полученных в резульате обаботки семи пунктов анкеты (пп 4, 8, 10, 15, 17).
Средней ценой ошибки назовем величину , где, как и ранее,
- матрица,
элементом которой является величина ошибки при классификации объекта
ого класса как объект
ого класса.
При обучении средняя цена ошибок алгоритма составила 0.52 и 0.83 на контроле. Так как алгоритм допустил значительно больше ошибок на обучении, чем на контроле, то уместно говорить о переобучении.
Отметим также то, что средняя цена ошибок алгоритма k взвешенных ближайших соседей, запущенный без отбора признаков, составила 0.77 при обучении и 0.68 на контроле.
Таким образом, алгоритм отбора признаков существенно снизил число с 24 до 5, понизив качество классификации.
Приведем результаты работы разных алгоритмов на данной выборке:
| Название алгоритма | Стоимость ошибкок при обучении | Стоимость ошибкок на контроле |
|---|---|---|
| Discrim | 0.509 | 0.535 |
| Quadisc | 0.431 | 0.619 |
| Logdisc | 0.499 | 0.538 |
| SMART | 0.389 | 0.601 |
| ALLOC80 | 0.597 | 0.584 |
| k-NN | 0.000 | 0.694 |
| k-NN,k=17, eucl,std | - | 0.411 |
| CASTLE | 0.582 | 0.583 |
| CART | 0.581 | 0.613 |
| IndCART | 0.069 | 0.761 |
| NewID | 0.000 | 0.925 |
| AC2 | 0.000 | 0.878 |
| Baytree | 0.126 | 0.778 |
| NaiveBay | 0.600 | 0.703 |
| CN2 | 0.000 | 0.856 |
| C4.5 | 0.640 | 0.985 |
| ITrule | * | 0.879 |
| Cal5 | 0.600 | 0.603 |
| Kohonen | 0.689 | 1.160 |
| DIPOL92 | 0.574 | 0.599 |
| Backprop | 0.446 | 0.772 |
| RBF | 0.848 | 0.971 |
| LVQ | 0.229 | 0.963 |
| WKNN, std | 0.770 | 0.732 |
| WKNN, std, Add | 0.516 | 0.839 |
Последние две строки таблицы - результат работы алгоритма, рассматриваемого в данной статье( WKNN, std - без отбора признаков, WKNN, std, Add - с отбором). Данные для построения таблицы взяты с http://www.is.umk.pl/projects/datasets-stat.html .
Исходный код
Скачать листинги алгоритмов можно здесь [1].
Смотри также
- Классификация
- Метрический классификатор
- Метод ближайших соседей
- Переобучение
- Скользящий контроль
- Численные методы обучения по прецедентам (практика, В.В. Стрижов)
Литература
- К. В. Воронцов, Лекции по метрическим алгоритмам классификации
- Bishop C. - Pattern Recognition and Machine Learning (Springer, 2006)
- The on-line textbook: Information Theory, Inference, and Learning Algorithms, by David J.C. MacKay.
- Abidin, T. and Perrizo, W. SMART-TV: A Fast and Scalable Nearest Neighbor Based Classifier for Data Mining. Proceedings of ACM SAC-06, Dijon, France, April 23-27, 2006. ACM Press, New York, NY, pp.536-540
- Wang, H. and Bell, D. Extended k-Nearest Neighbours Based on Evidence Theory. The Computer Journal, Vol. 47 (6) Nov. 2004, pp. 662-672.
- Yu, K. and Ji, L. Karyotyping of Comparative Genomic Hybridization Human Metaphases Using Kernel Nearest-Neighbor Algorithm, Cytometry 2002.
- UCI Machine Learning Repository, available on line at the University of California,Irvine http://www.ics.uci.edu/~mlearn/MLSum mary.html
| | Данная статья была создана в рамках учебного задания.
См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |