Анализ мультиколлинеарности (пример)

Материал из MachineLearning.

(Различия между версиями)

Текущая версия

Мультиколлинеарность — тесная корреляционная взаимосвязь между отбираемыми для анализа факторами, совместно воздействующими на общий результат, которая затрудняет оценивание регрессионных параметров.

Содержание

1 Постановка задачи
2 Описание алгоритма
- 2.1 Фактор инфляции дисперсии (VIF)
- 2.2 Методика Belsley, Kuh, и Welsch (BKW)
  - 2.2.1 Алгоритм BKW
3 Вычислительный эксперимент
4 Исходный код
5 Смотри также
6 Литература

Постановка задачи

Задана выборка $D = \{ y_i,\mathbf{x}_i\}_{i=1}^n$ признаков и зависимой переменной. Рассматривается линейная регрессионная модель вида:

$y_i=\sum_{j=1}^m b_j x_{ij} + \varepsilon_i, i=1,\dots,n$ Предполагается, что вектор регрессионных невязок имеет нулевое математическое ожидание и дисперсию $\sigma^2$ . Требуется создать инструмент исследования мультиколлинеарности признаков (методики VIF, Belsley) и проверить его работу на модельных данных.

Описание алгоритма

Фактор инфляции дисперсии (VIF)

Методика Belsley, Kuh, и Welsch (BKW)

Диагностика коллинеарности BKW основана на двух элементах, относящихся к $n \times p$ матрице данных $X$ использующейся в линейной регрессии $y = X \beta + \epsilon$ : индексы обусловленности(the scaled condition indexes) и дисперсионные доли(the variance-decomposition proportions). Оба этих диагностических элемента могут быть получены из сингулярного разложения (SVD) матрицы $X$ : $X=UD{V^{T}}$ , где ${U}^{T}U={V}^{T}V={I}_{p}$ и $D$ - диагональная с неотрицательными элементами ${\mu}_{1},...,{\mu}_{p}$ называющимися сингулярными числами $X$ . Индексы обусловленности это:
${\eta}_{k}\equiv\frac{{\mu}_{max}}{{\mu}_{k}}$ , $k=1,...,p$
${\eta}_{k} \geq 0$ для всех $k$ . Наибольший из индексов обусловленности это число обусловленности матрицы $X$ . Большое значение ${\eta}_{k}$ указывает на зависимость близкую к линейной между признаками и чем больше ${\eta}_{k}$ тем сильнее зависимость. Дисперсионные доли находятся из того факта, что используя SVD ковариационная матрица метода наименьших квадратов $b=(X^{T}X)^{-1}X^{T}y$ может записана как:

(3)

$V(b)={\sigma}^{2}(X^{T}X)^{-1} = {\sigma}^{2}V D^{-2} V^{T}$
где ${\sigma}^{2}$ это дисперсия возмущения $\varepsilon$ . Таким образом дисперсия $k$ -го регрессионного коэффициента ${b}_{k}$ это $k$ -й диагональный элемент (3):

(4)

$\mbox{var}({b}_{k})={\sigma}^{2} \sum_{j} {\frac{{\upsilon}^{2}_{kj}}{{\mu}^{2}_{j}}}$
где ${\mu}_{j}$ - сингулярные значения $X$ и $V\equiv({\upsilon}_{ij})$ . Определим $k, j$ -е дисперсионное соотношение как долю дисперсии $k$ -го регрессионного коэффициента связанная с $j$ -м компонентом его разложения (4). Доля считается как:
${\phi}_{kj}\equiv\frac{{\upsilon}^{2}_{kj}}{{\mu}^{2}_{j}}$ , ${\phi}_{k}\equiv\sum^{p}_{j=1} {\phi}_{kj}$ , $k=1,...,p$
Дисперсионное соотношение:
${\pi}_{jk}\equiv\frac{{\phi}_{kj}}{{\phi}_{k}}$ , $k,j=1,...,p$
Данные удобно представить в виде таблицы:

Condition index	$var({b}_{1})$	$var({b}_{2})$	$...$	$var({b}_{p})$
${\eta}_{1}$	${\pi}_{11}$	${\pi}_{12}$	...	${\pi}_{1p}$
${\eta}_{2}$	${\pi}_{11}$	...	...	${\pi}_{2p}$
.	.	.		.
.	.	.		.
.	.	.		.
${\eta}_{p}$	${\pi}_{p1}$	${\pi}_{11}$	...	${\pi}_{pp}$

Перед использованием BKW необходимо отмасштабировать матрицу $X$ . Стандартно применяется приведение столбцов к одинаковой длинне(норму). Будем рассматривать отмасштабированные индексы обусловленности $\stackrel{\sim}{{\eta}_{i}}(X)$ :
$X=[{X}_{1}\cdot\cdot\cdot{X}_{p}]<tex><br/> <tex>{s}_{i}\equiv{({X}^{T}_{i}{X}_{i})}^{-1/2}$
$S\equiv \mbox{diag}({s}_{1},...,{s}_{p})$
$\stackrel{\sim}{\eta}\equiv {\eta}_{i}(XS)$ , $i=1,...,p$

Алгоритм BKW

1. Стандартизация столбцов матрицы.
2. Вычисление индексов обусловленности и дисперсионных долей.
3. Определение количества зависимостей.
Превышение индексом обусловленности выбраного заранее порога означает наличие зависимости между признаками. Относительная сила зависимости определяется положение значения индекса обусловленности в прогресии 1, 3, 10, 30, 100, 300, 1000 итд.
4. Определение признаков участвующих в зависимости. 2 случая :
1) Только один достаточно большой индекс обусловленности - тогда возможно определение участвующих в зависимости признаков из дисперсионных долей: признак считается вовлеченным если его дисперсионная доля связанная с этим индексом превышает выбранный порог ${\pi}^{*}$ (обычно 0.25).
2) Есть несколько больших индексов обусловленности. В этом случае вовлеченность признака в зависимость определяется по сумме его дисперсионных долей отвечающих большим значениям индекса обусловленности - когда сумма превышает порог ${\pi}^{*}$ признак участвует как минимум в одной линейной зависимости.

Вычислительный эксперимент

В эксперименте используются модельные данные, для которых вычисляется VIF и матрица Belsley в зависимоти от параметра определяющего степень коллинеарности между признаками. Зависимость VIF и индексов обусловленности показана на графиках. Остальная часть таблицы BKW раскрашивалась (от темно-синего для 0 к темно-красному для 1) и создавалось видео показывающее ее изменение при параметре от 0 до 1.

Пример 1

Используются два ортогональных признака $x_1$ , $y_2$ и третий признак $y_1$ зависящий от параметра $k$ . При $k=0$ все признаки ортогональны, при увеличении $k$ зависимый признак $y_1$ приближается к $x_1$ , вплоть до полной коллинеарности при $k=1$ . Зависимость VIF от параметра:

Как видно из графика VIF $x_1$ и $y_1$ растет вплоть до бесконечности при $k=1$ , VIF $y_2$ при этом не изменен и равен 1.
Зависимость индексов обусловленности ${\eta}_{i}$ от $k$ :

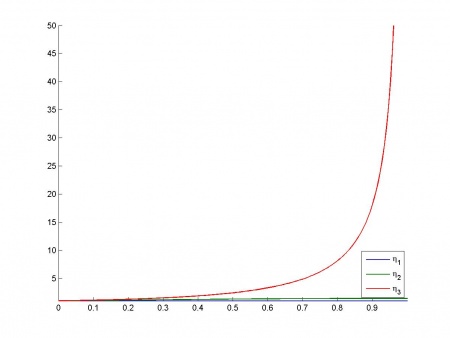
Таблица дисперсионных долей:

Видно что признаки $x_1$ и $y_1$ связаны усиляющейся зависимостью, и что других связей нет.

Пример 2

Используется неизменные признаки $x_1$ , $x_2$ и зависящие от параметра $k$ признаки $y_1$ , $y_2$ , $y_3$ . При $k=0$ все признаки ортогональны, при увеличении $k$ признаки $y_1$ , $y_2$ приближаются к $x_1$ , а $y_3$ - к $x_2$ вплоть до полной коллинеарности при $k=1$ .
Зависимость VIF от параметра:

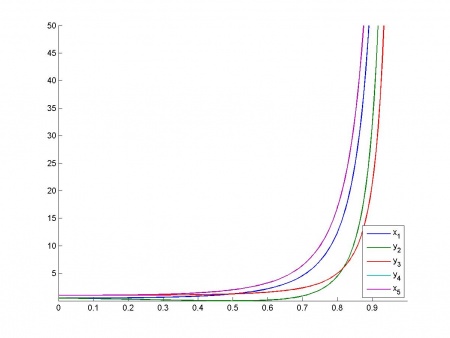
Зависимость индексов обусловленности ${\eta}_{i}$ от $k$ :

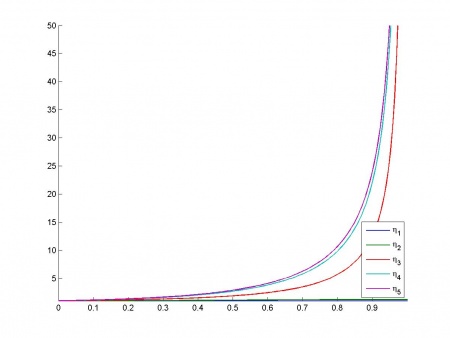
Таблица дисперсионных долей:

Наблюдается две основных зависимости - первая зависимость между признаками $x_1$ , $y_1$ , $y_2$ и вторая между признаками $x_2$ , $y_3$ .

Пример 3

Используются реальные данные. На них был проведен эксперимент по вычислению VIF и таблицы BKW.

#	VIF	#	VIF
1	1.21	7	3.82
2	1.31	8	7.43
3	1.69	9	3.46
4	1.51	10	1.47
5	19.27	11	1.97
6	16.37

У двух признаков значение фактора инфляции дисперсии больше 10, еще у одного больше 5. Такой результат — следствие их мультиколлинеарности относительно остальных признаков нашего набора.

Condition index	$var({b}_{1})$	$var({b}_{2})$	$var({b}_{3})$	$var({b}_{4})$	$var({b}_{5})$	$var({b}_{6})$	$var({b}_{7})$	$var({b}_{8})$	$var({b}_{9})$	$var({b}_{10})$	$var({b}_{11})$
1	0.0004	0.0006	0.0001	0.0001	0.0000	0.0000	0.0001	0.0001	0.0000	0.0000	0.0008
7.12	0.0031	0.0016	0.00016	0.0002	0.0001	0.0000	0.0251	0.0043	0.0000	0.0002	0.2885
9.03	0.0003	0.2262	0.0013	0.0007	0.0000	0.0010	0.0284	0.0154	0.0000	0.0001	0.1557
10.88	0.0149	0.3400	0.0003	0.0035	0.0022	0.01285	0.0007	0.0179	0.0000	0.0003	0.0380
14.14	0.9113	0.0819	0.0036	0.0003	0.0001	0.0001	0.0179	0.0001	0.0003	0.0004	0.0158
18.83	0.0233	0.2490	0.1015	0.0240	0.0032	0.0238	0.0240	0.0325	0.0105	0.0398	0.3721
26.77	0.0032	0.0063	0.6467	0.0012	0.0004	0.0268	0.0326	0.0897	0.0318	0.0296	0.0324
29.44	0.0316	0.0509	0.1138	0.9072	0.0000	0.0075	0.0504	0.0163	0.0073	0.0040	0.0128
34.04	0.0065	0.0026	0.0337	0.0310	0.0014	0.0211	0.0472	0.0863	0.0322	0.8635	0.0105
46.73	0.0043	0.0048	0.0009	0.0124	0.0460	0.0027	0.5990	0.7163	0.3045	0.0003	0.0468
101.67	0.0006	0.03557	0.0974	0.0190	0.9462	0.9036	0.1742	0.0207	0.613	0.0612	0.0261

Из таблицы видно что самому большому индексу обусловленности соответствует связь между 5, 6 и 9 признаками которым соответсвуют 19, 16 и 3 значения VIF. Также видна зависимость между 7 и 8 признаками - со значениями 3 и 7 VIF соответственно.

Исходный код

Cкачать листинги алгоритмов можно здесь [1]

Смотри также

Литература

Gianfranco Galmacci, Collinearity Detection in Linear Regression. Computational Economics 9:215-227, 1996.
D. A. Belsley, A Guide to Using the Collinearity Diagnostics. Computer Science in Economics and Management 4: 33-50, 1991.
Karen Callaghan and Jie Chen, Revisiting the Collinear Data Problem: An Assessment of Estimator 'Ill-Conditioning' in Linear Regression. Practical Assessment, Research & Evaluation, 2008, 13.

Данная статья была создана в рамках учебного задания.

Студент: Сунгуров Дмитрий

Преподаватель: В.В.Стрижов

Срок: 28 мая 2010

В настоящее время задание завершено и проверено. Данная страница может свободно правиться другими участниками проекта MachineLearning.ru.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://poligon.machinelearning.ru/wiki/index.php?title=%D0%90%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7_%D0%BC%D1%83%D0%BB%D1%8C%D1%82%D0%B8%D0%BA%D0%BE%D0%BB%D0%BB%D0%B8%D0%BD%D0%B5%D0%B0%D1%80%D0%BD%D0%BE%D1%81%D1%82%D0%B8_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»

Категории: Практика и вычислительные эксперименты | Линейная регрессия

@@ Строка 3: / Строка 3: @@
 Задана выборка <tex>D = \{ y_i,\mathbf{x}_i\}_{i=1}^n</tex> признаков и зависимой переменной. Рассматривается [[Линейная регрессия (пример)|линейная регрессионная модель]] вида:
-<tex>y_i=\sum_{j=1}^m w_j x_{ij} + \varepsilon_i, i=1,\dots,n</tex>
+<tex>y_i=\sum_{j=1}^m b_j x_{ij} + \varepsilon_i, i=1,\dots,n</tex>
 Предполагается, что вектор регрессионных невязок имеет нулевое математическое ожидание и дисперсию <tex>\sigma^2</tex>.
-Требуется создать инструмент исследования мультиколлинеарности признаков (методики VIF, Belsley) и исследовать устойчивость модели на зависимость параметров от дисперсии случайной переменной.
+Требуется создать инструмент исследования мультиколлинеарности признаков (методики VIF, Belsley) и проверить его работу на модельных данных.
 == Описание алгоритма ==
 === [[Фактор инфляции дисперсии|Фактор инфляции дисперсии (VIF)]] ===
-Дисперсия <tex>w_i</tex>:
-<tex>D\hat{w}_j=\frac{\sigma^2}{(n-1)D x_j}\frac{1}{1-R_j^2}.</tex>
+=== [[Метод Белсли|Методика Belsley, Kuh, и Welsch (BKW) ]]===
+Диагностика коллинеарности BKW основана на двух элементах, относящихся к <tex> n \times p</tex> матрице данных <tex>X </tex> использующейся в линейной регрессии <tex> y = X \beta + \epsilon</tex> : индексы обусловленности(the scaled condition indexes) и дисперсионные доли(the  variance-decomposition proportions). Оба этих диагностических элемента могут быть получены из сингулярного разложения (SVD) матрицы <tex>X</tex>: <tex> X=UD{V^{T}}</tex>, где <tex>{U}^{T}U={V}^{T}V={I}_{p}</tex> и <tex>D</tex> - диагональная с неотрицательными элементами <tex>{\mu}_{1},...,{\mu}_{p}</tex> называющимися сингулярными числами <tex>X</tex>. Индексы обусловленности это:<br />
-Первая дробь связана с дисперсией невязок и дисперсией векторов признаков. Вторая — фактор инфляции дисперсии, связанный с корреляцей данного признака с другими:
-<tex>VIF_j=\frac{1}{1-R_j^2},</tex>
-где <tex>R_j^2</tex> — [[коэффициент детерминации]] j-го признака относительно остальных:
-<tex>R_j^2 \equiv 1-{\sum_{i=1}^n (x_{ij} - \hat{x}_{ij})^2 \over \sum_{i=1}^n (x_{ij}-\bar{\mathbf{x}}_j)^2},\.</tex>
-Равенство единице фактора инфляции дисперсии говорит об ортогональности вектора значений признака остальным. Если значение <tex>VIF_j</tex> велико, то <tex>1-R^2_j</tex> — мало, то есть <tex>R_j^2</tex> близко к 1. Большие значения фактора инфляции дисперсии соответствуют почти линейной зависимости j-го столбца от остальных.
-=== [[Методика Belsley|Методика Belsley, Kuh, и Welsch (BKW) ]]===
-Диагностика Коллинеарности BKW основана на двух элементах, относящихся к <tex> n \times p</tex> матрице данных <tex>X </tex> использующейся в линейной регрессии <tex> y = X \beta + \varepsilon</tex> : индексы обусловленности(the scaled condition indexes) и дисперсионные доли(the  variance-decomposition proportions). Оба этих диагностических элемента могут быть получены из сингулярного разложения (SVD) матрицы <tex>X</tex>: <tex> X=UD{V^{T}}</tex>, где <tex>{U}^{T}U={V}^{T}V={I}_{p}</tex> и <tex>D</tex> - диагональная с неотрицательными элементами <tex>{\mu}_{1},...,{\mu}_{p}</tex> называющимися сингулярными числами <tex>X</tex>. Индексы обусловленности это:<br />
 <tex>{\eta}_{k}\equiv\frac{{\mu}_{max}}{{\mu}_{k}}</tex>, <tex>k=1,...,p</tex> <br />
-<tex>{\eta}_{k} \geq 0 </tex> для всех <tex>k</tex>. Большое значение <tex>{\eta}_{k}</tex> указывает на зависимость близкую к линейной между признаками и чем больше <tex>{\eta}_{k}</tex> тем сильнее зависимость. Дисперсионные доли находятся из того факта, что используя SVD ковариационная матрица метода наименьших квадратов <tex> b=(X^{T}X)^{-1}X^{T}y</tex> может записана как:<br /> <tex> V(b)={\sigma}^{2}(X^{T}X)^{-1} = {\sigma}^{2}V D^{-2} V^{T}</tex> (3)<br />
+<tex>{\eta}_{k} \geq 0 </tex> для всех <tex>k</tex>. Наибольший из индексов обусловленности это число обусловленности матрицы <tex>X</tex>. Большое значение <tex>{\eta}_{k}</tex> указывает на зависимость близкую к линейной между признаками и чем больше <tex>{\eta}_{k}</tex> тем сильнее зависимость. Дисперсионные доли находятся из того факта, что используя SVD ковариационная матрица метода наименьших квадратов <tex> b=(X^{T}X)^{-1}X^{T}y</tex> может записана как:<br />
-где <tex>{\sigma}^{2}</tex> это дисперсия возмущения <tex>\varepsilon</tex>. Таким образом дисперсия <tex>k</tex>-го регрессионного коэффициента <tex>{b}_{k}</tex> это <tex>k</tex>-й диогональный элемент (3): <br />
+{{eqno|3}}
+<tex> V(b)={\sigma}^{2}(X^{T}X)^{-1} = {\sigma}^{2}V D^{-2} V^{T}</tex><br />
-<tex>\mbox{var}({b}_{k})={\sigma}^{2}	\sum_{j} {\frac{{\upsilon}^{2}_{kj}}{{\mu}^{2}_{j}}}</tex>       (4)<br />
+где <tex>{\sigma}^{2}</tex> это дисперсия возмущения <tex>\varepsilon</tex>. Таким образом дисперсия <tex>k</tex>-го регрессионного коэффициента <tex>{b}_{k}</tex> это <tex>k</tex>-й диагональный элемент {{eqref|3}}: <br />
+{{eqno|4}}
+<tex>\mbox{var}({b}_{k})={\sigma}^{2}	\sum_{j} {\frac{{\upsilon}^{2}_{kj}}{{\mu}^{2}_{j}}}</tex><br/>
 где <tex>{\mu}_{j}</tex> - сингулярные значения <tex>X</tex> и <tex>V\equiv({\upsilon}_{ij})</tex>.
-Определим <tex>k, j</tex>-е дисперсионное соотношение как долю дисперсии <tex>k</tex>-го регрессионного коэффициента связанная с <tex>j</tex>-м компонентом его разложения (4). Доля считается как:<br/>
+Определим <tex>k, j</tex>-е дисперсионное соотношение как долю дисперсии <tex>k</tex>-го регрессионного коэффициента связанная с <tex>j</tex>-м компонентом его разложения {{eqref|4}}. Доля считается как:<br/>
 <tex>{\phi}_{kj}\equiv\frac{{\upsilon}^{2}_{kj}}{{\mu}^{2}_{j}}</tex>,
 <tex>{\phi}_{k}\equiv\sum^{p}_{j=1} {\phi}_{kj}</tex>, <tex>k=1,...,p</tex><br/>
@@ Строка 72: / Строка 62: @@
 == Вычислительный эксперимент ==
-Эксперимент проводится на модельных данных.
+В эксперименте используются модельные данные, для которых вычисляется VIF и матрица Belsley в зависимоти от параметра определяющего степень коллинеарности между признаками. Зависимость VIF и индексов обусловленности показана на графиках. Остальная часть таблицы BKW раскрашивалась (от темно-синего для 0 к темно-красному для 1) и создавалось видео показывающее ее изменение при параметре от 0 до 1.
+===Пример 1===
+Используются два ортогональных признака <tex>x_1</tex>, <tex>y_2</tex> и третий признак <tex>y_1</tex> зависящий от параметра <tex>k</tex>. При <tex>k=0</tex> все признаки ортогональны, при увеличении <tex>k</tex> зависимый признак <tex>y_1</tex> приближается к <tex>x_1</tex>, вплоть до полной коллинеарности при <tex>k=1</tex>.
+Зависимость VIF от параметра:<br/>
+[[Изображение:plot3vif.jpg|450px]]<br/>
+Как видно из графика VIF <tex>x_1</tex> и <tex>y_1</tex> растет вплоть до бесконечности при <tex>k=1</tex>, VIF <tex>y_2</tex> при этом не изменен и равен 1.<br/>
+Зависимость индексов обусловленности <tex>{\eta}_{i}</tex> от <tex>k</tex>:<br/>
+[[Изображение:plot3sci.jpg|450px]]<br/>
+Таблица дисперсионных долей:<br/>
+{|
+ |<videoflash type="youtube">zeugEKkLhnY</videoflash>
+ |}<br/>
+Видно что признаки <tex>x_1</tex> и <tex>y_1</tex> связаны усиляющейся зависимостью, и что других связей нет.
+===Пример 2===
+Используется неизменные признаки <tex>x_1</tex>, <tex>x_2</tex> и зависящие от параметра <tex>k</tex> признаки <tex>y_1</tex>,<tex>y_2</tex>,<tex>y_3</tex>. При <tex>k=0</tex> все признаки ортогональны, при увеличении <tex>k</tex> признаки <tex>y_1</tex>, <tex>y_2</tex> приближаются к <tex>x_1</tex>, а <tex>y_3</tex> - к <tex>x_2</tex> вплоть до полной коллинеарности при <tex>k=1</tex>.<br/>
+Зависимость VIF от параметра:<br/>
+[[Изображение:plot2vif.jpg|450px]]<br/>
+Зависимость индексов обусловленности <tex>{\eta}_{i}</tex> от <tex>k</tex>:<br/>
+[[Изображение:plot2sci.jpg|450px]]<br/>
+Таблица дисперсионных долей:<br/>
+{|
+ |<videoflash type="youtube">2rdv55kh6JU</videoflash>
+ |}<br/>
+Наблюдается две основных зависимости - первая зависимость между признаками <tex>x_1</tex>, <tex>y_1</tex>, <tex>y_2</tex> и вторая между признаками <tex>x_2</tex>, <tex>y_3</tex>.
+===Пример 3===
+Используются [http://www-stat.stanford.edu/~hastie/Papers/LARS/ реальные данные]. На них был проведен эксперимент по вычислению VIF и таблицы BKW.
+{| class="wikitable" style="text-align: center;"
+|- bgcolor="#ccccc"
+! width=30 % |#
+! width=40 % |VIF
+! width=30 % |#
+! width=40 % |VIF
+|-
+| '''1''' || 1.21 || '''7''' || 3.82
+|-
+| '''2''' || 1.31 || '''8''' || 7.43
+|-
+| '''3''' || 1.69 || '''9''' || 3.46
+|-
+| '''4''' || 1.51 || '''10''' || 1.47
+|-
+| '''5''' || 19.27 || '''11''' || 1.97
+|-
+| '''6''' || 16.37 || ''' ''' || ''' '''
+|-
+|}
+У двух признаков значение фактора инфляции дисперсии больше 10, еще у одного больше 5. Такой результат — следствие их мультиколлинеарности относительно остальных признаков нашего набора.
+{| class="wikitable" style="text-align: center;"
+|- bgcolor="#ccccc"
+! width=70 % |Condition index
+! width=50 % |<tex>var({b}_{1}) </tex>
+! width=50 % |<tex>var({b}_{2}) </tex>
+! width=50 % |<tex>var({b}_{3}) </tex>
+! width=50 % |<tex>var({b}_{4}) </tex>
+! width=50 % |<tex>var({b}_{5}) </tex>
+! width=50 % |<tex>var({b}_{6}) </tex>
+! width=50 % |<tex>var({b}_{7}) </tex>
+! width=50 % |<tex>var({b}_{8}) </tex>
+! width=50 % |<tex>var({b}_{9}) </tex>
+! width=50 % |<tex>var({b}_{10}) </tex>
+! width=50 % |<tex>var({b}_{11}) </tex>
+|-
+| 1 || 0.0004 || 0.0006 || 0.0001 || 0.0001 || 0.0000 || 0.0000 || 0.0001 || 0.0001 || 0.0000 || 0.0000 || 0.0008
+|-
+| 7.12 || 0.0031 || 0.0016 || 0.00016 || 0.0002 || 0.0001 || 0.0000 || 0.0251 || 0.0043 || 0.0000 || 0.0002 || 0.2885
+|-
+| 9.03 || 0.0003 || 0.2262 || 0.0013 || 0.0007 || 0.0000 || 0.0010 || 0.0284 || 0.0154 || 0.0000 || 0.0001 || 0.1557
+|-
+| 10.88 || 0.0149 || 0.3400 || 0.0003 || 0.0035 || 0.0022 || 0.01285 || 0.0007 || 0.0179 || 0.0000 || 0.0003 || 0.0380
+|-
+| 14.14 || 0.9113 || 0.0819 || 0.0036 || 0.0003 || 0.0001 || 0.0001 || 0.0179 || 0.0001 || 0.0003 || 0.0004 || 0.0158
+|-
+| 18.83 || 0.0233 || 0.2490 || 0.1015 || 0.0240 || 0.0032 || 0.0238 || 0.0240 || 0.0325 || 0.0105 || 0.0398 || 0.3721
+|-
+| 26.77 || 0.0032 || 0.0063 || 0.6467 || 0.0012 || 0.0004 || 0.0268 || 0.0326 || 0.0897 || 0.0318 || 0.0296 || 0.0324
+|-
+| 29.44 || 0.0316 || 0.0509 || 0.1138 || 0.9072 || 0.0000 || 0.0075 || 0.0504 || 0.0163 || 0.0073 || 0.0040 || 0.0128
+|-
+| 34.04 || 0.0065 || 0.0026 || 0.0337 || 0.0310 || 0.0014 || 0.0211 || 0.0472 || 0.0863 || 0.0322 || 0.8635 || 0.0105
+|-
+| '''46.73''' || 0.0043 || 0.0048 || 0.0009 || 0.0124 || 0.0460 || 0.0027 || '''0.5990''' || '''0.7163''' || 0.3045 || 0.0003 || 0.0468
+|-
+| '''101.67''' || 0.0006 || 0.03557 || 0.0974 || 0.0190 || '''0.9462''' || '''0.9036''' || 0.1742 || 0.0207 || '''0.613''' || 0.0612 || 0.0261
+|-
+|}
+Из таблицы видно что самому большому индексу обусловленности соответствует связь между 5, 6 и 9 признаками которым соответсвуют 19, 16 и 3 значения VIF. Также видна зависимость между 7 и 8 признаками - со значениями 3 и 7 VIF соответственно.
 == Исходный код ==
-*Cкачать листинги алгоритмов можно здесь [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/MCA//]
+*Cкачать листинги алгоритмов можно здесь [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Group774/Sungurov2010Multicollinearity/]
 == Смотри также ==
@@ Строка 83: / Строка 163: @@
 * [[Линейная регрессия (пример)]]
 * [[Сингулярное разложение]]
+* [[Метод Белсли]]
 == Литература ==
-* Gianfranco Galmacci, Collinearity Detection in Linear Regression. M: 1996 Kluwer Academic Publishers.
+* Gianfranco Galmacci, Collinearity Detection in Linear Regression. Computational Economics 9:215-227, 1996.
-* D. A. BELSLEY, A  Guide  to  Using  the  Collinearity  Diagnostics. M: 1991 Kluwer Academic  Publishers.
+* D. A. Belsley, A  Guide  to  Using  the  Collinearity  Diagnostics. Computer Science in Economics and Management 4: 33-50, 1991.
-* К. В. Воронцов, Лекции по линейным алгоритмам классификации и регрессии
+* Karen Callaghan and  Jie Chen, Revisiting the Collinear Data Problem: An Assessment of Estimator 'Ill-Conditioning' in Linear Regression. Practical Assessment, Research & Evaluation, 2008, 13.
+{{ЗаданиеВыполнено|Сунгуров Дмитрий|В.В.Стрижов|28 мая 2010|e1ekt|strijov}}
-{{Задание|Сунгуров Дмитрий|В.В.Стрижов|28 мая 2010}}
 [[Категория:Практика и вычислительные эксперименты]]
 [[Категория:Линейная регрессия]]