Участник:Riabenko/Песочница
Материал из MachineLearning.
м |
м |
||
| Строка 25: | Строка 25: | ||
Изображение:LSD_mu2.png|Точность оценки параметра <tex>\mu</tex> и ширина доверительного интервала для неё. | Изображение:LSD_mu2.png|Точность оценки параметра <tex>\mu</tex> и ширина доверительного интервала для неё. | ||
</gallery> | </gallery> | ||
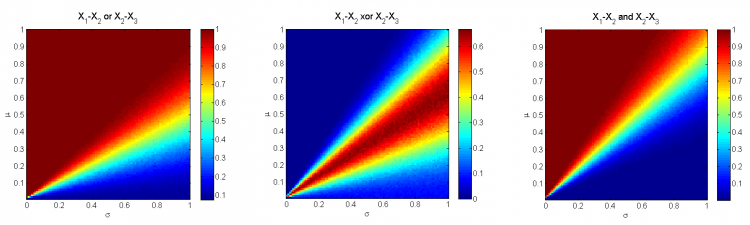
| - | Можно считать, что метод детектирует значимую на уровне <tex>\alpha=0.05</tex> разность между средними значениями выборок, если соответствующий 95% доверительный интервал для неё не содержит нуля. Рассмотрим для каждой пары значений параметров <tex>\mu, \sigma</tex> доли выборок, на которых разница в <tex>\mu</tex> между средними пар выборок <tex>X_1, X_2</tex> и <tex>X_2 | + | Можно считать, что метод детектирует значимую на уровне <tex>\alpha=0.05</tex> разность между средними значениями выборок, если соответствующий 95% доверительный интервал для неё не содержит нуля. Рассмотрим для каждой пары значений параметров <tex>\mu, \sigma</tex> доли выборок, на которых разница в <tex>\mu</tex> между средними пар выборок <tex>X_1, X_2</tex> и <tex>X_2, X_3</tex> была детектирована. |
| - | <gallery widths=" | + | <gallery widths="750px" heights="250px"> |
| - | Изображение:LSD_3.png| | + | Изображение:LSD_3.png|Доли выборок с детектитуемыми различиями между средними при различных значениях <tex>\mu</tex> и <tex>\sigma</tex>. |
</gallery> | </gallery> | ||
| - | + | Заметим, что при <tex>\mu<\sigma</tex> достаточно велик шанс детектировать различия между средними только одной из двух абсолютно равнозначных пар выборок – в конусе <tex>0.4\sigma\leq\mu\leq 0.9\sigma</tex> вероятность такого события составляет 0.4-0.6. | |
| + | |||
| + | Оценим долю выборок, на которых была детектирована разница между средними выборок <tex>X_1, X_3</tex>: | ||
<gallery widths="250px" heights="250px"> | <gallery widths="250px" heights="250px"> | ||
| + | Изображение:LSD_2mu.png/Мощность метода LSD при детекции различий между средними значениями выборок <tex>X_1, X_3</tex>. | ||
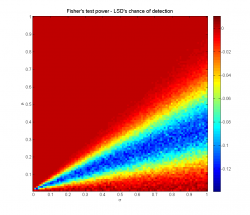
Изображение:Fpow-LSD3.png|Разность эмпирических оценок мощностей критерия Фишера и метода ЛСД для детекции различия между средними выборок <tex>X_1, X_3</tex>. | Изображение:Fpow-LSD3.png|Разность эмпирических оценок мощностей критерия Фишера и метода ЛСД для детекции различия между средними выборок <tex>X_1, X_3</tex>. | ||
</gallery> | </gallery> | ||
| + | Сравнивая последний график с построенными оценками мощности критерия Фишера, можно заметить, что метод ЛСД обладает большей чувствительностью к разнице между средними значениями выборок. Различия заметны в области <tex>\sigma/10\leq\mu\leq\sigma/2</tex>, где мощность критерия Фишера может быть ниже более, чем на 0.12: | ||
Версия 22:28, 29 октября 2012
Задание 2. Исследование свойств многомерного статистического метода на модельных данных
Пример
Исследуем чувствительность однофакторного дисперсионного анализа к расстояниям между выборками и дисперсиям выборок.
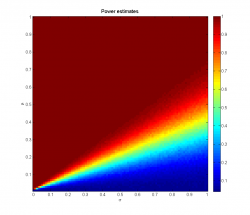
Посмотрим, как от расстояний между выборками и дисперсий зависят средний достигаемый уровень значимости и мощность используемого по умолчанию критерия Фишера:
Для каждой пары значений параметров мощность оценивается как доля выборок, на которых нулевая гипотеза о равенстве всех средних была отвергнута.
Зависимость выглядит естественно: мощность растёт при увеличении расстояний между выборками и уменьшении их дисперсий. Для данного размера выборок средний достигаемый уровень значимости не превосходит 0.05 для всех значений , мощность при этом не опускается ниже 0.7.
Для сгенерированных выборок проведём сравнение средних при помощи метода LSD. Для каждой пары средних метод даёт точечную оценку разности между ними и 95% доверительный интервал для этой разности. Так как
, для оценки параметра
можно использовать среднее между оценками
и
.
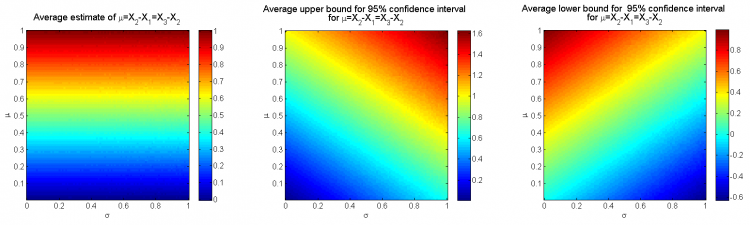
Рассмотрим усреднённые оценки и границы доверительных интервалов:
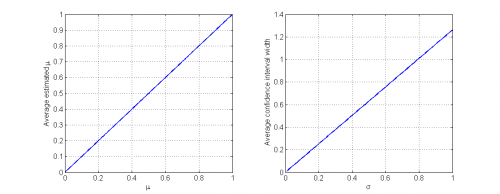
Заметим, что усреднённая точечная оценка расстояния между выборками является точной и не зависит от дисперсии выборок, а ширина доверительного интервала для
, напротив, зависит только от
:
Можно считать, что метод детектирует значимую на уровне разность между средними значениями выборок, если соответствующий 95% доверительный интервал для неё не содержит нуля. Рассмотрим для каждой пары значений параметров
доли выборок, на которых разница в
между средними пар выборок
и
была детектирована.
Заметим, что при достаточно велик шанс детектировать различия между средними только одной из двух абсолютно равнозначных пар выборок – в конусе
вероятность такого события составляет 0.4-0.6.
Оценим долю выборок, на которых была детектирована разница между средними выборок :
Сравнивая последний график с построенными оценками мощности критерия Фишера, можно заметить, что метод ЛСД обладает большей чувствительностью к разнице между средними значениями выборок. Различия заметны в области , где мощность критерия Фишера может быть ниже более, чем на 0.12: