Участник:Stsupkov
Материал из MachineLearning.
(→Заключение) |
(→Классификация рядов из контрольной выборки) |
||
| (2 промежуточные версии не показаны) | |||
| Строка 99: | Строка 99: | ||
== Заключение == | == Заключение == | ||
| - | В данной работе был построен классификатор для повышения точности прогнозирования временных рядов. Для тестирования классификатора были сгенерированы модельные данные разной природы с разной степенью зашумления. Определены удобные структуры данных и написаны функции, заполняющие их. Для определения тренда и сезонности был реализован алгоритм непараметрического выделения с учетом пропусков в данных и | + | В данной работе был построен классификатор для повышения точности прогнозирования временных рядов. Для тестирования классификатора были сгенерированы модельные данные разной природы с разной степенью зашумления. Определены удобные структуры данных и написаны функции, заполняющие их. Для определения тренда и сезонности был реализован алгоритм непараметрического выделения с учетом пропусков в данных и длины выборки, некратной периоду. |
Было изучено поведение многих адаптивные модели для краткосрочного прогнозирования, написаны реализации этих моделей. На модельных данных сравнивалось качество прогнозирования при разной степени зашумления, при данных, не соответствующих модели. | Было изучено поведение многих адаптивные модели для краткосрочного прогнозирования, написаны реализации этих моделей. На модельных данных сравнивалось качество прогнозирования при разной степени зашумления, при данных, не соответствующих модели. | ||
| Строка 115: | Строка 115: | ||
| + | <!-- комментарий, чтобы было удобнее редактировать | ||
| Строка 124: | Строка 125: | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | --> | ||
| + | |||
| + | = Уточнение признакового пространства и выбор семейства алгоритмов = | ||
| + | |||
| + | |||
| + | == Выделение дополнительных признаков == | ||
| + | Признаковое пространство пополнилось. Признаки были поделены на три группы: пропуски, тренд, сезонность. | ||
| + | |||
| + | === Пропуски === | ||
| + | Попытаемся посмотреть на пропуски в рядах с человеческой точки зрения. В глаза бросаются длинные серии отсутствующих данных и много небольших. В признаке "средняя длина пропусков" с разными весами учитываются большие пробелы в данных и точечные отсутствия прогнозов в какие-то дни. Посмотрим на связь между средней длиной и долей пропусков. | ||
| + | |||
| + | [[Изображение:Tsupkov_2_1_1.png]] | ||
| + | |||
| + | Из графиков следует, что у 17 ряда пропусков меньше других, но идут они одной большой группой (на графике - в конце ряда). Отсюда же у 8 ряда в сумме пропусков больше, но они больше разрежены по длине ряда: | ||
| + | |||
| + | {| | ||
| + | |[[Изображение:Tsupkov_2_1_2.png]] | ||
| + | |[[Изображение:Tsupkov_2_1_3.png]] | ||
| + | |} | ||
| + | |||
| + | Такой признак удобен тем, что ряд можно разбить на подряды и уже работать с ними. | ||
| + | |||
| + | === Тренд === | ||
| + | Для формирования признаков, описывающих поведение тренда, была предпринята попытка использовать статистику Манн-Кендалла. | ||
| + | |||
| + | Тест Манн-Кендалла работает не очень стабильно. Даже для одномерного случая статистика Манн-Кендалла далека от ожидаемого распределения. Статистика T асимптотически стремится к нормальному распределению с нулевым мат. ожиданием и известной большой дисперсией (дисперсия растет как куб от числа измерений), если в независимой выборке отсутствует тренд. Для экспериментов генерировался равномерный шум, и даже для достаточно больших временных рядов в распределении часто было сложно увидеть нормальное. | ||
| + | |||
| + | Проверим гипотезу о том, что T имеет нормальное распределение. Разделив вариационный ряд на ожидаемую дисперсию, предполагаем получить стандартное нормальное распределение. Проверим 0-гипотезу с помощью критерия Колмогорова-Смирнова. В большинстве случаев гипотеза нормальности отвергается даже при достаточно большом доверительном интервале, что говорит о том, что метод очень неустойчив. | ||
| + | |||
| + | В качестве признака берутся вероятности исходов из критерия Колмогорова и критерия хи-квадрат. Критерий хи-квадрат принимает гипотезу о нормальности чаще. | ||
| + | |||
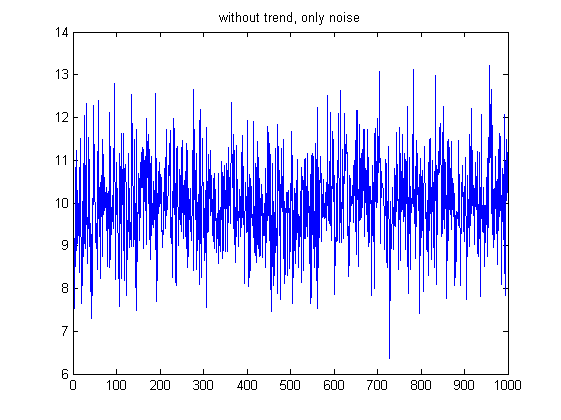
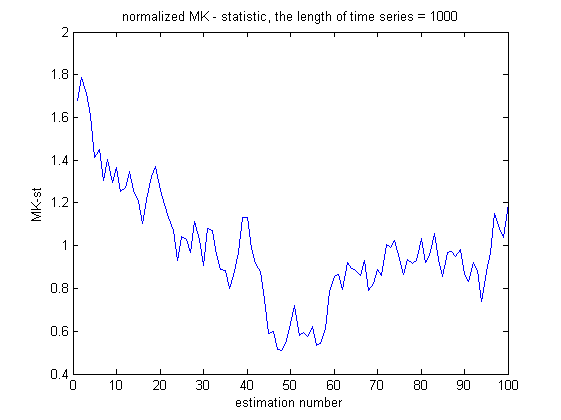
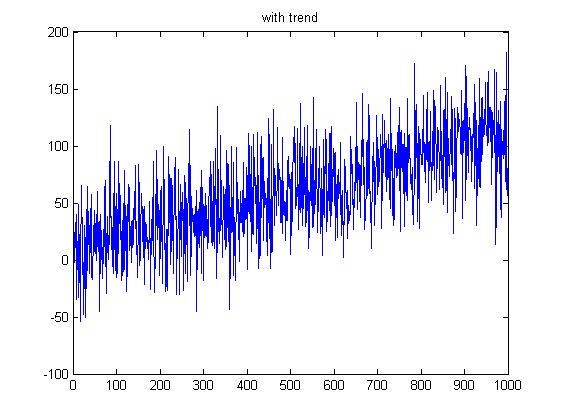
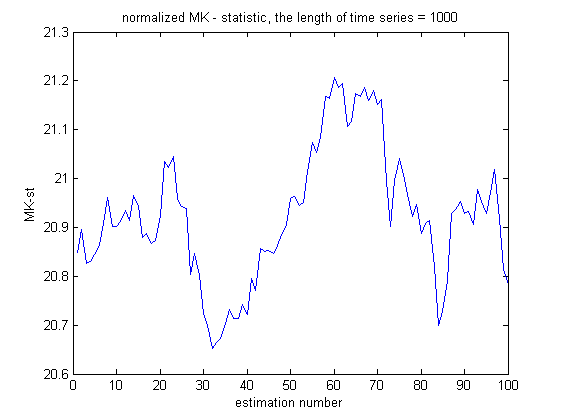
| + | На графиках - сравнение поведения статистики в случае наличия тренда и в случае просто шума. Для удобства вариационный ряд уже был поделен на стандартное отклонение (чтобы избежать огромных чисел на графиках). Видно, что если тренд есть, то статистика гораздо "дальше" от нормального распределения. | ||
| + | |||
| + | {| | ||
| + | |+ Поведение статистике на ряде без тренда | ||
| + | |[[Изображение:Tsupkov_2_2_1.png]] | ||
| + | |[[Изображение:Tsupkov_2_2_2.png]] | ||
| + | |} | ||
| + | |||
| + | {| | ||
| + | |+ Поведение статистики на ряде с трендом | ||
| + | |[[Изображение:Tsupkov_2_2_3.png]] | ||
| + | |[[Изображение:Tsupkov_2_2_4.png]] | ||
| + | |} | ||
| + | |||
| + | === Сезонность === | ||
| + | Попробуем сначала выделить тренд, убрав две сезонности - годовую и недельную - с помощью непараметрического выделения сезонности. | ||
| + | |||
| + | Предположим, что тренд линейный. Найдем тангенс угла наклона линейной регрессией. Пополним признаки ошибкой и тангенсом угла. | ||
| + | |||
| + | [[Изображение:Tsupkov_2_3_1.png]] | ||
| + | |||
| + | == Классификация рядов из контрольной выборки == | ||
| + | |||
| + | Классификация проводится с помощью SVM. SVM разбивает алгоритмы из контрольной выборки на несколько классов. Последовательно выделяются классы объектов, которые лучше всего выделяются i-ым алгоритмом. При таком подходе некоторые ряды остаются без классификации. Ниже приведена таблица классификации контрольной выборки (ряды*алгоритмы): | ||
| + | |||
| + | <code> | ||
| + | 0 0 34 0 0 | ||
| + | 0 0 0 0 36 | ||
| + | 0 0 0 0 0 | ||
| + | 0 0 0 0 36 | ||
| + | 0 0 0 0 36 | ||
| + | 0 0 0 0 36 | ||
| + | 18 0 0 35 0 | ||
| + | 18 27 34 35 0 | ||
| + | 0 0 0 0 0 | ||
| + | 0 0 0 0 36 | ||
| + | 0 0 0 0 0 | ||
| + | 0 0 0 0 0 | ||
| + | 0 0 0 0 36 | ||
| + | </code> | ||
| + | |||
| + | По строкам выбираются лучшие алгоритмы, оставшие классифицируются ближайшим соседом. Ожидается, что в алгоритмах, где SVM ничего не мог сказать, возможны грубые ошибки. В нашем примере это ряды с номерами 23, 42, 44, 48. Построим для них оптимальные прогнозы и прогнозы классификатора. В тех местах, где график предсказаний один, выбор классификатора совпал с оптимальным алгоритмом. Действительно, на 23 и на 44 ряде модель определилась совсем неправильно: | ||
| + | |||
| + | {| | ||
| + | |+ Примеры ситуаций, в которых ожидалась ошибка алгоритма | ||
| + | |[[Изображение:Tsupkov_2_4_1.png|700px]] | ||
| + | |[[Изображение:Tsupkov_2_4_2.png|700px]] | ||
| + | |} | ||
| + | |||
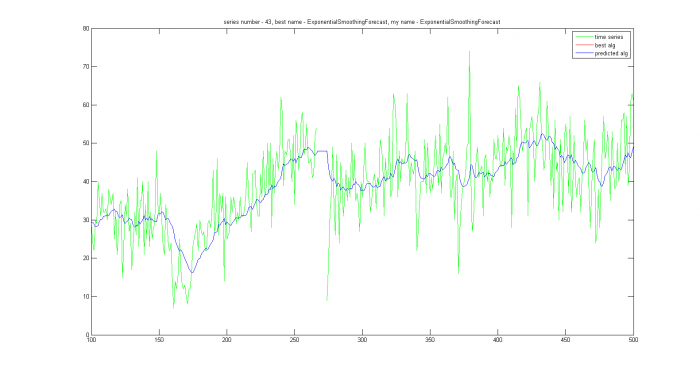
| + | На остальных рядах ожидалась правильная работа алгоритма. Все спрогнозированные ряды можно поделить на две группы: где модель была выбрана правильно, но алгоритм не оптимален и где верная и модель, и алгоритм. В заголовках графиков есть название лучшего и предсказываемого алгоритма. | ||
| + | |||
| + | {| | ||
| + | |+ Примеры ситуаций, в которых модель выбирается правильно, алгоритмы из модели - не оптимально | ||
| + | |[[Изображение:Tsupkov_2_4_3.png|700px]] | ||
| + | |[[Изображение:Tsupkov_2_4_4.png|700px]] | ||
| + | |} | ||
| + | |||
| + | {| | ||
| + | |+ Примеры ситуаций, в которых правильно выбрана и модель, и алгоритм | ||
| + | |[[Изображение:Tsupkov_2_4_5.png|700px]] | ||
| + | |[[Изображение:Tsupkov_2_4_6.png|700px]] | ||
| + | |} | ||
| + | |||
| + | == План дальнейшей работы == | ||
| + | * Необходимо пополнить признаковое пространство | ||
| + | * Расширить множество базовых алгоритмов | ||
| + | * Попробовать разбить исходный ряд на подряды, которые прогнозируются лучше | ||
[[Категория:Страницы участников]] | [[Категория:Страницы участников]] | ||
Текущая версия
Содержание |
Построение экспериментального стенда для исследования задачи классификации временных рядов с целью повышения качества прогнозирования
Введение
Временной ряд — это собранный в разные моменты времени статистический материал о значении каких-либо параметров. Временные ряды являются одиним из самых важных объектов в области машинного обучения. Прогнозирование временных рядов широко используется в самых разных областях человеческой деятельности.
Временной ряд содержит в себе достаточно много информации. Выявление структуры временного ряда необходимо для того, чтобы построить математическую модель того явления, которое описывается рядом. Прогноз временного ряда используется для эффективного принятия решений.
В этой работе проводятся исследования алгоритма, классифицирующего временные ряды на основе выделенных признаков, подбирающего наиболее адекватную модель для прогноза. Также приводятся результаты его работы на модельных данных и сравнение качества классификации с некоторыми другими моделями выбора наиболее подходящего алгоритма прогнозирования.
Постановка задачи
Главная цель исследования — повысить качество прогнозирования временных рядов. Имеется алгоритм или композиция алгоритмов для прогнозирования временных рядов. Ряды имеют экономическую природу, поэтому у них довольно много характерных особенностей: недельная, месячная и годовая сезонность, обычно выделяется тренд. Данные сильно зашумлены, и имеют много пропусков.
Очень часто встречается ситуация, что ряд в целом хорошо прогнозируется одним базовым алгоритмом, но данные бывают зашумлены настолько, что сложный алгоритм начинает давать неадекватные прогнозы, настраиваясь на шум и выбросы. Такие ситуации возникают не на всей выборке, а, как правило, только лишь на некотором небольшом участке ряда, поэтому интересно знать, будет ли базовая модель хорошо работать на одном небольшом участке и имеет ли смысл настраиваться на шум, вместо того чтобы попробовать применить более простую модель, иногда даже самую простую, такую как экспоненциальное сглаживание.
На вход классификатору подаются два множества: временные ряды в общем случае произвольной длины и алгоритмы прогнозирования. Рядов имеется порядка ста, алгоритмов порядка тридцати. На выходе классификатор определяет, какие модели лучше подходят для прогнозирования этих рядов, или дает отказ от классификации. Исследуемые объекты — временные ряды — случайно разбиваются на два множества: обучение и контроль. Для того чтобы сформировать на обучающей выборке вектор из правильных ответов, полным перебором ищется алгоритм из семейства на входе с наилучшим качеством прогнозирования. Но поступить таким же образом с конрольной выборкой нельзя, потому что время работы основного алгоритма прогнозирования, в который впоследствии будет интегрирован разрабатываемый модуль, будет неприемлемо большим. Для сокращения времени работы формируется признаковое пространство, на основе которого проводится классификация.
Актуальность
Любая задача прогнозирования начинается с выбора математической модели. Если данные не сильно зашумлены, то, скорее всего, удачно выбранная по обучающей выборке модель будет адекватно работать и на контрольной выборке. В условиях реальных задач это бывает далеко не всегда. Переобученный алгоритм может потерять как качество прогнозирования, так и скорость работы.
Актуальность исследуемой проблемы обусловлена тем, что ситуации, когда модель плохо применима или совсем неприменима, встречаются достаточно часто. С другой стороны, решить эту задачу, перебрав все алгоритмы, нельзя, если не увеличивать вычислительную мощность. Выбирая, корректируя алгоритм прогнозирования "на лету", происходит сильная экономия вычислительных ресурсов.
Кроме того, имея информацию о том, когда базовый алгоритм прогнозирования перестает корректно работать, мы получаем новые данные об исследуемом временном ряде. На их основе можно выделять новые признаки в пространстве временных рядов и классифицировать их.
Описание работы классификатора
Входные данные: временные ряды
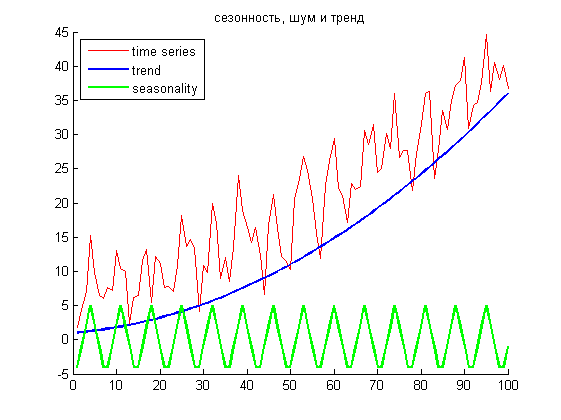
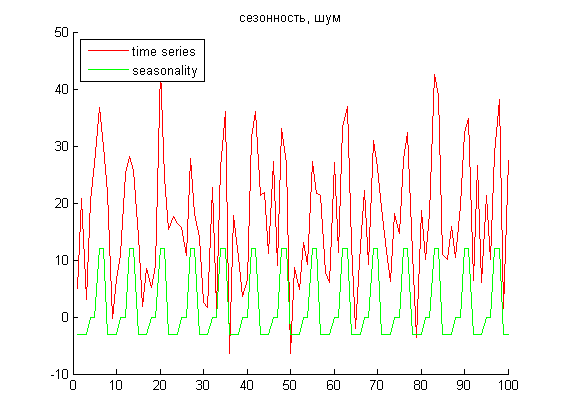
Модельные входные данные генерировались по нескольким моделям. По разным комбинациям наличия или отсутствия тренда или сезонности временные ряды можно разделить на четыре группы.
Пример временных рядов с недельной пилообразной сезонностью и полиномиальным трендом и без тренда, но с недельной сезонностью.
Таким образом, входные данные представляют собой матрицу, у которой количество строк равняется количеству временных рядов. На текущем этапе для удобства хранения и генерирования предполагается, что все ряды имеют одинаковую длину, но это не обязательно. Также пока будем предполагать, что данные без пропусков.
Входные данные: алгоритмы прогнозирования
Исследуемые алгоритмы загружаются в классификатор из отдельного файла, где они хранятся в виде массива структур. Для каждой модели прогнозирования, например, Тейла-Вейджа, экспоненциального среднего, Брауна, могут быть несколько алгоритмов классификации, различающихся только параметрами. Первичная информация об алгоритмах (имя, параметры, указатель на функцию и количество) хранится в структуре AlgList:
AlgList =
name: {'My_Exp' 'My_Exp' 'My_Holt'}
param: {[1x1 struct] [1x1 struct] [1x1 struct]}
hand: {[@(x,y)My_Exp(x,y)] [@(x,y)My_Exp(x,y)] [@(x,y)My_Holt(x,y)]}
amount: 3
Для каждого алгоритма и для каждого временного ряда строится матрица оценок качества прогнозирования алгоритмов на исходных временных рядах. Качество прогнозирования рассчитывается двумя способами: как средний модуль отклонения и как среднее квадратичное отклонение от истинного значения.
Обучение и классификация
Из рядов случайным образом формируется обучающая и контрольная выборка. Для обучающей выборки правильная метка — номер наиболее удачного алгоритма — рассчитывается по матрице оценок, для каждой строки ищется минимум ошибок относительно выбранного функционала качества:
[~, Classes.classif(train)] = min(Quality(train, :), [], 2);
По рядам формируется признаковое пространство: выборочная дисперсия, наличие тренда, сезонности, доля пропусков в данных. Методом взвешенного ближайшего соседа считается принадлежность к тому или иному классу.
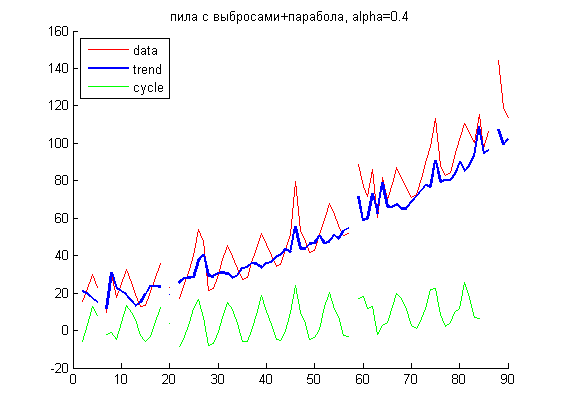
Сезонность выделялась непараметрически. Будем считать, что исходный ряд можно представить y(t) = x(t) + s(t), где x – тренд, а s – сезонность. Сезонность на каждом периоде характеризуется логичными допущениями, что значения на концах периода совпадают, а интеграл по периоду равен 0. Тогда если каким-то образом удастся выделить сезонность, тренд получится ее вычитанием из исходного ряда с возможным сглаживанием впоследствии. Пусть имеются измерения на каждом из периодов. Введем оценочную функцию, определенную на том же множестве, что и наш временной ряд. В каждой точке она равна экспоненциальному среднему из имеющихся значений ряда для аналогичных сдвигов относительно периода (так как в ряде могут быть пропуски, суммировать будем только то, что есть). Вторая производная этой функции совпадает со второй производной прогнозируемой сезонности, поэтому s(t) есть сумма введенной функции и еще двух слагаемых a+b*t, где a и b — константы. Найти их можно из определения сезонности, данного выше. Единственный параметр алгоритма — константа регуляризации, как и в экспоненциальном сглаживании показывает значимость измерений, лежащих в соседних слева и справа периодах.
Сравнительная оценка качества классификаторов
Для оценки качества полученного классификатора рассмотрим еще несколько моделей выбора алгоритма прогнозирования. Вернемся к исходной задаче: есть участок, где базовый алгоритм работает плохо, поэтому надо понять, имеет ли смысл настраивать параметры алгоритма точнее, или можно применить что-то более простое.
Самый простой путь решения — в спорных ситуациях использовать один и тот же универсальный алгоритм, например, экспоненциально среднее. Но во многих случаях его усовершенствования, такие как модель Хольта и прочие, будут работать гораздо лучше, что подтверждается экспериментами.
Другой путь решения — выбирать нужный алгоритм, сравнивая качество классификации с остальными алгоритмами. В реальности использовать такой алгоритм возможности нет, но для того, чтобы оценить, дает ли построенный классификтор какие-то приемущества перед одной фиксированной моделью, может быть полезен. Метки, которые раздает такой «идеальный» классификатор, получаются из уже найденной матрицы оценок взятием минимума по строкам. Также модель можно выбирать по скользящему контролю.
Последняя модель для сравнения — созданный классификатор.
Поскольку каждая из моделей может давать очень хорошие результаты на каком-то классе рядов и очень плохие на других, логично для каждой модели брать среднее по всем функциям потерь на контрольной выборке. Сейчас для подсчета объективной оценки средней ошибки сравниваемых моделей бралось среднее арифметическое, но в общем случае это может быть и более сложная конструкция.
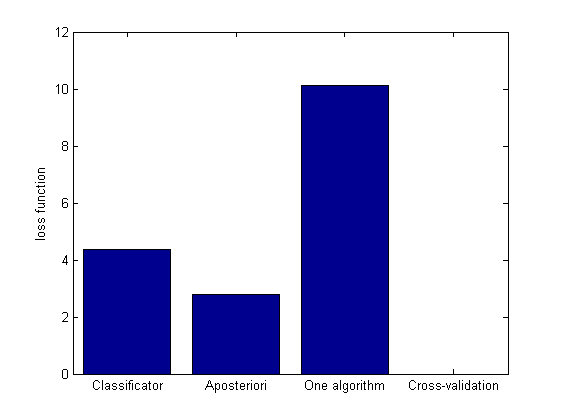
Результаты работы удобно представлять в виде столбчатой диаграммы.
Из диаграммы видно, что если классифицировать всю выборку одним алгоритмом, экспоненциальным средним, более чем в два раза хуже, чем подбирать модели с помощью классификатора.
В программе для каждой модели хранится вектор для ее классификации Classes и вектор функций потерь Res:
classif: [50x1 double]
apost: [50x1 double]
onealg: [50x1 double]
crossv: [50x1 double]
Заключение
В данной работе был построен классификатор для повышения точности прогнозирования временных рядов. Для тестирования классификатора были сгенерированы модельные данные разной природы с разной степенью зашумления. Определены удобные структуры данных и написаны функции, заполняющие их. Для определения тренда и сезонности был реализован алгоритм непараметрического выделения с учетом пропусков в данных и длины выборки, некратной периоду.
Было изучено поведение многих адаптивные модели для краткосрочного прогнозирования, написаны реализации этих моделей. На модельных данных сравнивалось качество прогнозирования при разной степени зашумления, при данных, не соответствующих модели.
В дальнейшем необходимо усовершенствовать качество оценки классификатора, подобрать новые функции для оценивания средних потерь. Требуется изучить другие методы классификации и сравнить их между собой. Необходимо придумать богатое признаковое пространство, которое позволит более точно охарактеризовать ряд.
Список литературы
- Лукашин Ю. П., Адаптивные методы краткосрочного прогнозирования временных рядов
- Губанов В. А., Непараметрическое выделение динамических сезонных циклов
- Цыплаков А. А., Основы прогнозирования временных рядов
Уточнение признакового пространства и выбор семейства алгоритмов
Выделение дополнительных признаков
Признаковое пространство пополнилось. Признаки были поделены на три группы: пропуски, тренд, сезонность.
Пропуски
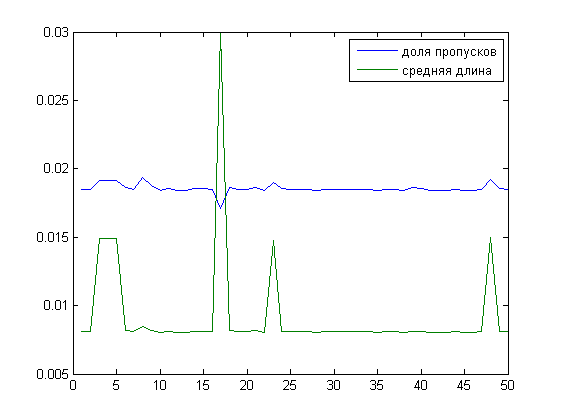
Попытаемся посмотреть на пропуски в рядах с человеческой точки зрения. В глаза бросаются длинные серии отсутствующих данных и много небольших. В признаке "средняя длина пропусков" с разными весами учитываются большие пробелы в данных и точечные отсутствия прогнозов в какие-то дни. Посмотрим на связь между средней длиной и долей пропусков.
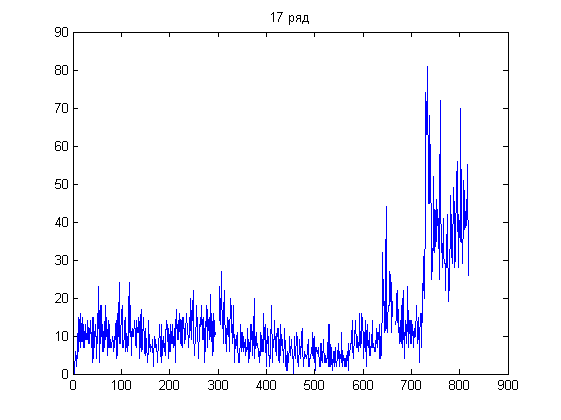
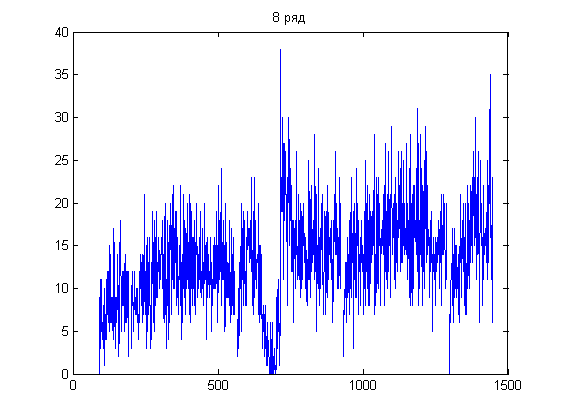
Из графиков следует, что у 17 ряда пропусков меньше других, но идут они одной большой группой (на графике - в конце ряда). Отсюда же у 8 ряда в сумме пропусков больше, но они больше разрежены по длине ряда:
| 
|
Такой признак удобен тем, что ряд можно разбить на подряды и уже работать с ними.
Тренд
Для формирования признаков, описывающих поведение тренда, была предпринята попытка использовать статистику Манн-Кендалла.
Тест Манн-Кендалла работает не очень стабильно. Даже для одномерного случая статистика Манн-Кендалла далека от ожидаемого распределения. Статистика T асимптотически стремится к нормальному распределению с нулевым мат. ожиданием и известной большой дисперсией (дисперсия растет как куб от числа измерений), если в независимой выборке отсутствует тренд. Для экспериментов генерировался равномерный шум, и даже для достаточно больших временных рядов в распределении часто было сложно увидеть нормальное.
Проверим гипотезу о том, что T имеет нормальное распределение. Разделив вариационный ряд на ожидаемую дисперсию, предполагаем получить стандартное нормальное распределение. Проверим 0-гипотезу с помощью критерия Колмогорова-Смирнова. В большинстве случаев гипотеза нормальности отвергается даже при достаточно большом доверительном интервале, что говорит о том, что метод очень неустойчив.
В качестве признака берутся вероятности исходов из критерия Колмогорова и критерия хи-квадрат. Критерий хи-квадрат принимает гипотезу о нормальности чаще.
На графиках - сравнение поведения статистики в случае наличия тренда и в случае просто шума. Для удобства вариационный ряд уже был поделен на стандартное отклонение (чтобы избежать огромных чисел на графиках). Видно, что если тренд есть, то статистика гораздо "дальше" от нормального распределения.
| 
|
| 
|
Сезонность
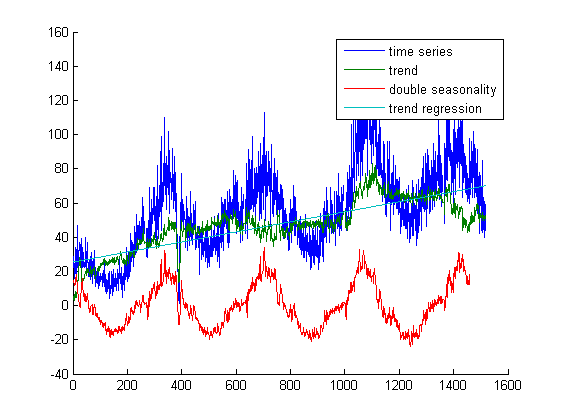
Попробуем сначала выделить тренд, убрав две сезонности - годовую и недельную - с помощью непараметрического выделения сезонности.
Предположим, что тренд линейный. Найдем тангенс угла наклона линейной регрессией. Пополним признаки ошибкой и тангенсом угла.
Классификация рядов из контрольной выборки
Классификация проводится с помощью SVM. SVM разбивает алгоритмы из контрольной выборки на несколько классов. Последовательно выделяются классы объектов, которые лучше всего выделяются i-ым алгоритмом. При таком подходе некоторые ряды остаются без классификации. Ниже приведена таблица классификации контрольной выборки (ряды*алгоритмы):
0 0 34 0 0
0 0 0 0 36
0 0 0 0 0
0 0 0 0 36
0 0 0 0 36
0 0 0 0 36
18 0 0 35 0
18 27 34 35 0
0 0 0 0 0
0 0 0 0 36
0 0 0 0 0
0 0 0 0 0
0 0 0 0 36
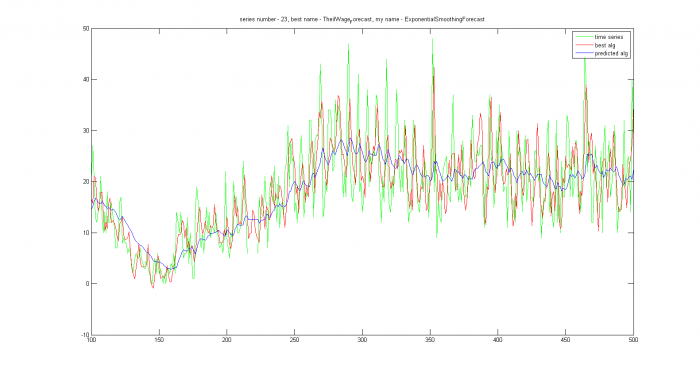
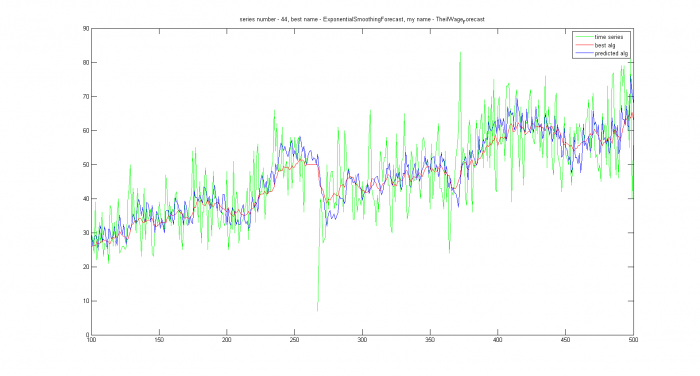
По строкам выбираются лучшие алгоритмы, оставшие классифицируются ближайшим соседом. Ожидается, что в алгоритмах, где SVM ничего не мог сказать, возможны грубые ошибки. В нашем примере это ряды с номерами 23, 42, 44, 48. Построим для них оптимальные прогнозы и прогнозы классификатора. В тех местах, где график предсказаний один, выбор классификатора совпал с оптимальным алгоритмом. Действительно, на 23 и на 44 ряде модель определилась совсем неправильно:
| 
|
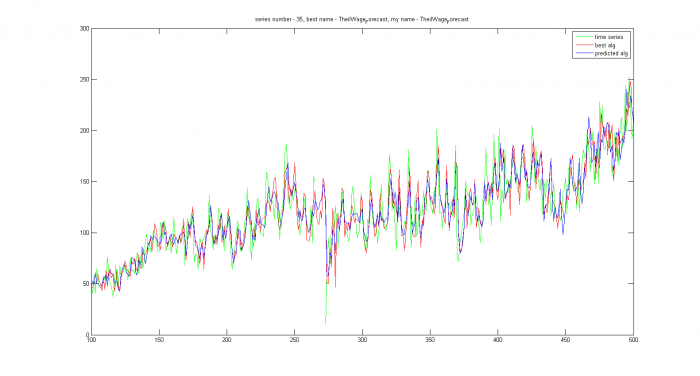
На остальных рядах ожидалась правильная работа алгоритма. Все спрогнозированные ряды можно поделить на две группы: где модель была выбрана правильно, но алгоритм не оптимален и где верная и модель, и алгоритм. В заголовках графиков есть название лучшего и предсказываемого алгоритма.

| 
|
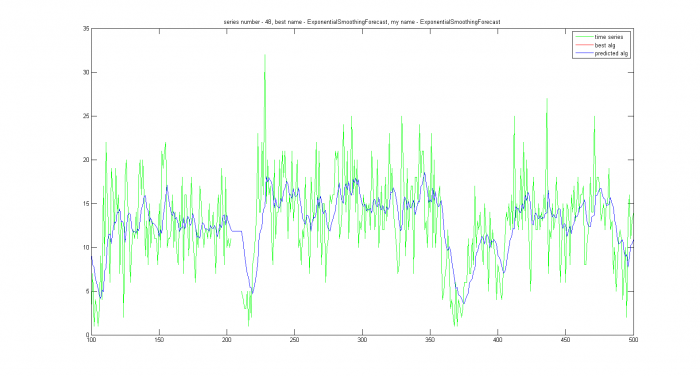
| 
|
План дальнейшей работы
- Необходимо пополнить признаковое пространство
- Расширить множество базовых алгоритмов
- Попробовать разбить исходный ряд на подряды, которые прогнозируются лучше