Статистический анализ данных (курс лекций, К.В.Воронцов)/2010

Материал из MachineLearning.

(Различия между версиями)

Текущая версия

Содержание

1 Задание 1. Исследование свойств одномерных статистических критериев на модельных данных
- 1.1 Пример задания
- 1.2 Задания
2 Задание 2. Анализ реальных данных
3 Ссылки

Задание 1. Исследование свойств одномерных статистических критериев на модельных данных

Необходимо провести исследование одного или нескольких классических критериев проверки статистических гипотез. Интерес представляет поведение достигаемого уровня значимости (p-value) как функции размера выборок и параметров распределения. В соответствии с индивидуальными параметрами задания необходимо указанным способом сгенерировать одну или несколько выборок из заданного распределения, выполнить проверку гипотезы при помощи соответствующего критерия, а затем многократно повторить эту процедуру для различных значений параметров. По результатам расчётов необходимо построить требуемые в задании графики, среди которых могут быть следующие:

график зависимости достигаемого уровня значимости от значений параметров при однократном проведении эксперимента;
график зависимости достигаемого уровня значимости от значений параметров, усреднённого по большому количеству повторений эксперимента (например, по 100, 500, 1000 повторений);
график с эмпирическими оценками мощности критерия для разных значений параметров.

В качестве оценки мощности принимается доля отвержений нулевой гипотезы среди всех проверок. То есть, если эксперимент повторялся $k$ раз для каждого набора значений параметра, и в $m$ из $k$ случаев гипотеза была отвергнута на некотором фиксированном уровне значимости $\alpha$ (примем $\alpha=0.05$ ), оценкой мощности будет отношение $m/k$ .

Необходимо сдать: выполненный в LaTex или Microsoft Word отчёт с описанием алгоритма, построенными графиками и выводами (объяснение полученных результатов моделирования, границы применимости критерия и т.д.), а также *.m-файл, при запуске которого на экран выводятся графики, соответствующие имеющимся в отчёте (допускается, хотя и не рекомендуется использование среды R).

Задание принимается до первого ноября.

Пример задания

Исследуем поведение классического двухвыборочного критерия Стьюдента для проверки гипотезы однородности против альтернативы сдвига при разных значениях параметров.

$x^n = (x_1,\ldots,x_n)\sim N(\mu_1,\sigma),\;\; y^n = (y_1,\ldots,y_n)\sim N(\mu_2,\sigma);$

$H_0\,:\; \mu_1=\mu_2,$

$H_1\,:\; \mu_1\neq\mu_2.$

$\sigma = 1; \;\;\; \mu_1=0; \;\;\; \mu_2=0\,:\,0.05\,:\,3; \;\;\; n=5\,:\,1\,:\,50.$

При каждом значении $\mu_2$ выборки для разных значений $n$ генерируются независимо.

График 1: значения достигаемого уровня значимости при однократной генерации выборок.

График 2: значения достигаемого уровня значимости, усрёднённые по 100 экспериментам.

График 3: значения эмпирических оценок мощности критерия при проведении 100 экспериментов ( $\alpha=0.05$ ).

Задания

Анализ устойчивости критериев к нарушению предположений

Исследовать устойчивость одновыборочного критерия Стьюдента к нарушению предположения о нормальности данных. $x^n$ — смесь распределений $N(\mu,1)$ и $U[-a+\mu,a+\mu]$ с весами $p$ и $1-p$ соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит $p$ , то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного). Для разных значений параметров выборки генерируются независимо.
$H_0\,:\; \mu=0, \;\; H_1\,:\; \mu\neq 0;$
$p=0\,:\,0.02\,:\,1; \;\; \mu=-1\,:\,0.05\,:\,1; \;\; n=100.$
Построить графики вида 1, 2, 3, сделать выводы о чувствительности критерия к зашумлению выборки.

Студент 1: $a=1.$

Студент 2: $a=5.$

Студент 3: $a=10.$

Исследовать устойчивость двухвыборочного критерия Стьюдента для независимых выборок к нарушению предположения о нормальности данных. $x^n \sim N(\mu_1,1),$ $y^n$ — смесь распределений $N(\mu_2,1)$ и $U[-a+\mu_2,a+\mu_2]$ с весами $p$ и $1-p$ соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит $p$ , то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного). Для разных значений параметров выборки генерируются независимо.
$H_0\,:\; \mu_1=\mu_2, \;\; H_1\,:\; \mu_1\neq\mu_2;$
$\mu_1=0; \;\; p=0\,:\,0.02\,:\,1; \;\; \mu_2=-1\,:\,0.05\,:\,1; \;\; n=100.$
Построить графики вида 1, 2, 3, сделать выводы о чувствительности критерия к зашумлению одной из выборок.

Студент 4: $a=1.$

Студент 5: $a=5.$

Студент 6: $a=10.$

Анализ чувствительности критериев к редактированию выборки

Известно, что исключение из выборки определённых наблюдений зачастую может достаточно сильно повлиять на результат анализа. Необходимо исследовать чувствительность одновыборочного критерия критерия Стьюдента к редактированию выборки.
$x^n \sim N(\mu,\sigma);$
$H_0\,:\; \mu=0, \;\;\; H_1\,:\; \mu>0.$
При каждом значении параметра $\mu$ генерируется выборка размера $n$ , проводится проверка гипотезы $H_0$ , затем по некоторому правилу из выборки исключается один из элементов, проверка гипотезы повторяется, затем исключается ещё один, и т.д. Обозначим за $K$ максимальное число исключённых в таком процессе элементов. Построить графики вида 1, 2, 3, сделать выводы о чувствительности критерия к редактированию выборки.

Студент 7: $n=100;\;\;K=50;\;\;\sigma=1;\;\;\mu=-1\,:\,0.01\,:\,1;\;\;$ на каждом шаге исключается максимальный элемент.

Студент 9: $n=200;\;\;K=100;\;\;\sigma=5;\;\;\mu=-2\,:\,0.02\,:\,2;\;\;$ на каждом шаге исключается максимальный элемент.

Студент 10: $n=100;\;\;K=50;\;\;\sigma=2;\;\;\mu=-2\,:\,0.02\,:\,2;\;\;$ на каждом шаге исключается минимальный элемент.

Студент 11: $n=200;\;\;K=100;\;\;\sigma=5;\;\;\mu=-3\,:\,0.03\,:\,3;\;\;$ на каждом шаге исключается минимальный элемент.

Анализ поведения схожих критериев

Требуется исследовать поведение указанной пары статистических критериев, подходящих для решения одной и той же задачи, сравнить мощность и достигаемые уровни значимости и сделать выводы о границах применимости критериев. Необходимо для каждого из критериев построить графики зависимости достигаемых уровней значимости и оценок мощностей от параметров, и показать, в каких областях изменения параметров предпочтительнее использовать тот или иной критерий. Выбрать вид графиков так, чтобы различия между критериями были видны наиболее ясно (например, график вида 4).

График 4: значения эмпирических оценок мощности критериев при проведении 100 экспериментов.

$x^n \sim N(0,1),\;\;y^n \sim N(\mu,1);$
$H_0\,:\; \mu=0, \;\;\; H_1\,:\; \mu\neq 0;$
$\mu=-2\,:\,0.02\,:\,2;\;\; n=10\,:\,5\,:\,100.$

Студент 12: двухвыборочный критерий Стьюдента для независимых выборок и критерий Уилкоксона-Манна-Уитни.

Студент 13: двухвыборочный критерий Стьюдента для связных выборок и критерий Уилкоксона для связных выборок.

Студент 14: двухвыборочные критерий Стьюдента для связных и независимых выборок.

Студент 15: критерий Уилкоксона-Манна-Уитни и медианный критерий.

Студент 16: критерий Уилкоксона для связных выборок и критерий знаков.

Студент 8: критерий знаков и медианный критерий.

$x^n \sim Be(p_1),\;\;y^n \sim Be(p_2);$
$a = \sum_{n}I$x_i=1$,\;\; b = \sum_{n}I$x_i=0$,\;\; c = \sum_{n}I$y_i=1$,\;\; d = \sum_{n}I$y_i=0$;$
$H_0\,:$ связь между признаками в таблице сопряжённости 2×2, задаваемой величинами $a, b, c, d,$ отсутствует; $\;\;\; H_1\,:$ признаки связаны между собой.

Студент 17: критерий хи-квадрат и точный критерий Фишера. $p_1=0\,:\,0.02\,:\,1; \;\; p_2=0\,:\,0.02\,:\,1; \;\;n=50.$

Студент 18: критерий хи-квадрат и точный критерий Фишера. $p_1=0.5; \;\; p_2=0\,:\,0.05\,:\,1; \;\;n=10\,:\,2\,:\,50.$

$x^n$ — смесь распределений $N(0,1)$ и $U[-a,a]$ с весами $p$ и $1-p$ соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит $p$ , то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного).
$H_0\,:\; x \sim N(0,1), \;\;\; H_1\,:\; H_0$ неверна;
$p=0\,:\,0.02\,:\,1; \;\; n=10\,:\,5\,:\,100.$

Студент 19: критерий Шапиро-Уилка и критерий Колмогорова-Смирнова. $a=1.$

Студент 20: критерий омега-квадрат и критерий Шапиро-Уилка. $a=2.$

Студент 21: критерий хи-квадрат и критерий омега-квадрат. $a=5.$

Студент 22: критерий Колмогорова-Смирнова и критерий хи-квадрат. $a=7.$

Задание 2. Анализ реальных данных

Ниже приведены описания анализируемых данных и постановки задач. Сами данные каждый студент может получить по электронной почте сразу после сдачи первого задания. При проведении анализа можно пользоваться любыми доступными программными средствами. Необходимо предоставить подробный письменный отчёт по проведённому исследованию, содержащий выводы и описания каждого этапа анализа — используемые методы, обоснование их применимости, промежуточные результаты вычислений, графики. Помимо выводов, касающихся математических особенностей решения, необходимо включить в отчёт заключения, сформулированные в терминах предметной области, которые могли бы быть понятны гипотетическому заказчику-нематематику.

Задание принимается с 1 по 20 декабря. Напоминаю, что сдача задания является необходимым условием получения допуска к экзамену — студенты, не получившие зачёт по второму заданию к моменту сдачи экзамена, не смогут его сдавать, и должны будут выполнить задание к пересдаче. Среди студентов, сдающих задание после 20 декабря, проводится конкурс: последние трое сдавших зачёт получат на экзамене дополнительный билет, основанный на материалах курса, но не входящий в основной список вопросов.

Летальность пациентов с сепсисом

По 454 пациентам с сепсисом (лихорадка, тахикардия, тахипноэ и острая недостаточность по крайней мере одной системы органов) имеются следующие данные: оценка начального состояния по шкале APACHE острых и хронических функциональных изменений, факт наступления смерти в течение 30 дней после начала исследования (для каждого значения APACHE score приведены общее число пациентов в таком состоянии и соответствующее число пациентов, умерших в течение 30 дней).

Студент 7: оценить вероятность наступления в 30-дневный срок летального исхода в зависимости от исходного состояния. Построить функции, дающие точечную оценку и границы 95% доверительного интервала.

Линейные размеры тысячефранковых банкнот

Банкнота в 1000 швейцарских франков серии, действовавшей в период с 1911 по 1958. Красным обозначены измеренные величины.

Имеются данные измерений двухсот швейцарских тысячефранковых банкнот, бывших в обращении в первой половине XX века. Сто из банкнот были настоящими, а сто - поддельными. Измерены следующие величины: $X_1$ — длина банкноты, $X_2$ —ширина банкноты с левой стороны, $X_3$ —ширина банкноты с правой стороны, $X_4$ —расстояние от нижнего края до рамки рисунка, $X_5$ — расстояние от нижнего края до рамки рисунка, $X_6$ — длина диагонали рисунка.

Студент 12: построить функцию, оценивающую по данным измерений вероятность того, что имеющаяся банкнота фальшивая, и 95% доверительный интервал для этой вероятности.

Студент 15: построить функции, оценивающие вероятность того, что имеющаяся банкнота фальшивая, по признакам $X_1-X_3$ и по признакам $X_4-X_6$ . Сравнить эффективность выявления фальшивых купюр по двум группам признаков, сделать выводы.

Ценообразование бриллиантов

Имеются данные о цене и потребительских качествах 308 бриллиантов, продававшихся в Сингапуре в 2000 году. Известны: вес бриллианта в каратах, цвет (закодирован буквами латинского алфавита: наиболее чистый цвет — буквой D, менее чистые — буквами E, F, G и т.д., чем ближе к концу алфавита, тем "грязнее"), группа чистоты (отсутствие дефектов, профессиональная оценка, выдаваемая специалистами при исследовании бриллианта в лупу десятикратного увеличения; бриллианты без трещин и включений получают оценку IF ("internally flawless"), далее в порядке убывания чистоты следуют группы VVS1 и VVS2 ("very very slightly imperfect"), VS1 и VS2 ("very slightly imperfect")), название организации, выдавшей сертификат по группе чистоты (GIA — Gemmological Institute of America, IGI — International Gemmological Institute, HRD — Hoge Raad Voor Diamant), стоимость бриллианта в сингапурских долларах.

Студент 13: построить модель ценообразования бриллиантов, учитывая все особенности имеющихся данных.

Студент 8: отличается ли средняя цена бриллиантов, сертифицированных различными организациями?

Студент 16: какой признак более значимо влияет на цену бриллиантов — цвет или чистота?

Студент 14: существует общепринятая система классификации бриллиантов на мелкие — до 0.29 карата, средние — от 0.30 до 0.99 карата и крупные — свыше 1 карата. Достаточно ли для предсказания цены знать о весе бриллианта только к какому классу он относится, или предсказания с использованием знаний о точном весе значимо лучше?

Счета за электроэнергию

Имеются помесячные данные о тратах на электроэнергию одного фиксированного домохозяйства на среднем западе США. За каждый месяц 1991-2000 годов приведены затраты на электроэнергию в долларах. Для объяснения колебаний размера счёта приведены следующие переменные: среднемесячная температура по данным последних тридцати лет, погодные индексы CDD и HDD (CDD - Cooling Degree Day - количество градусов, на которые средняя дневная температура больше 65°F, взятое суммой за все дни месяца; HDD - Heating Degree Day - аналогично, суммарное количество градусов, на которое средняя дневная температура меньше 65°F), число проживающих в доме членов семьи, индикатор установки нового счётчика, индикаторы установки двух новых тепловых насосов, объём потребления электроэнергии в киловатт-часах.

Студент 2: предсказать объём потребления и затраты на электроэнергию в каждом месяце 2001 года.

Студент 9: оценить влияние установки нового оборудования на объём потребления и затраты на электроэнергию.

Студент 10: построить функцию, предсказывающую затраты на электроэнергию по температуре, погодным индексам и числу проживающих в доме.

Кассовые сборы кинофильмов

Рассматриваются 428 фильмов с наибольшими кассовыми сборами в истории (по данным boxofficemojo.com). По каждому фильму известны: название, студия, на которой он был снят, суммарные кассовые сборы, сборы в США и в остальном мире по отдельности, год выхода, индикатор повторного выхода картины в прокат.

Студент 18: сравнить по всем подходящим признакам фильмы студий Warner Bros., Buena Vista, Universal, Fox, Paramount и Sony (в совокупности ими снято 324 фильма из рассматриваемых 428). Есть ли значимые отличия между продукцией этих студий по какому-либо из признаков?

Студент 22: построить функцию, оценивающую сборы фильма за пределами США, по сборам в США, названию студии, году выпуска и индикатору повторного выхода в прокат.

Студент 11: есть ли связь между сборами фильма и годом выхода на экраны? Использовав дополнительную информацию о среднегодовой цене билета, привести кассовые сборы рассматриваемых фильмов к ценам 2010 года. Оценить связь между преобразованными сборами фильма и годом выхода на экраны.

Нормальная температура тела

У 130 испытуемых были измерены температура тела и пульс, записаны также данные о поле испытуемых.

Студент 6: построить функцию для оценки температуры по пульсу и полу испытуемого.

Студент 4: построить функцию для оценки пульса по температуре тела и полу испытуемого.

Студент 5: построить функцию, предсказывающую, какого пола испытуемый, на основе результатов измерений пульса и температуры, оценить надёжность такого предсказания.

Вкус воды

У 106 испытуемых, пришедших на праздник университета Лонгвуд, выяснили, какую воду они обычно пьют - бутилированную, фильтрованную или водопроводную. По каждому из опрошенных имеются также данные о поле, возрасте и предпочитаемой марке бутилированной воды, если такая есть. После опроса испытуемым предложили расставить в порядке ухудшения вкусовых качеств четыре образца воды - марок Fiji, Sam’s Choice, Aquafina и обычную водопроводную воду, причём ни сами испытуемые, ни опрашивающие не знали, какой образец какую воду содержит (двойной слепой тест).

Студент 19: исследовать распределение приоритетов по результатам двойного слепого теста, рассмотреть связь между результатами теста и заявленными предпочтениями.

Студент 1: отличаются ли мужчины и женщины по заявленным предпочтениям или результатам слепого теста?

Студент 21: верно ли, что испытуемые, пьющие бутилированную воду, дают более низкие оценки водопроводной воде, чем все остальные? Верно ли, что те, кто пьёт фильтрованную воду, дают ей более низкие оценки, чем те, кто пьёт водопроводную?

Эффективность тромболитической терапии

Собраны данные по 206 пациентам второго кардиологического отделения московской городской клинической больницы №25. Имеются результаты 14 анализов, а также 8 дополнительных признаков, описывающих пациента (пол, возраст, курение, наличие диабета и т.д.)

Студент 20: построить функцию, оценивающую вероятность выздоровления пациента в результате тромболитической терапии по приведённым 22 признакам.

Студент 3: построить функцию, оценивающую вероятность возникновения осложнений у пациента в результате тромболитической терапии по приведённым 22 признакам.

Студент 17: оценить влияние курения на вероятности выздоровления и возникновения осложнений, а также на результаты 14 анализов.

Ссылки

Источник — «http://poligon.machinelearning.ru/wiki/index.php?title=%D0%A1%D1%82%D0%B0%D1%82%D0%B8%D1%81%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7_%D0%B4%D0%B0%D0%BD%D0%BD%D1%8B%D1%85_%28%D0%BA%D1%83%D1%80%D1%81_%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D0%B9%2C_%D0%9A.%D0%92.%D0%92%D0%BE%D1%80%D0%BE%D0%BD%D1%86%D0%BE%D0%B2%29/2010»

Категория: Учебные курсы

@@ Строка 1: / Строка 1: @@
-= Задание 1. Исследование статистических критериев на модельных данных  =
+{{TOCright}}
-Необходимо провести исследование одного из классических критериев проверки статистических гипотез. Интерес представляет поведение
+= Задание 1. Исследование свойств одномерных статистических критериев на модельных данных  =
-[[Достигаемый уровень значимости|достигаемого уровня значимости]] (p-value) как функции размера выборок и параметров распределения. В соответствии с индивидуальными параметрами задания необходимо сгенерировать одну или несколько выборок из указанного распределения, выполнить [[Проверка статистических гипотез|проверку гипотезы]] при помощи соответствующего критерия, а затем многократно повторить эту процедуру для различных значений параметров. При этом, в зависимости от индивидуальных особенностей задания, выборки могут как генерироваться заново для каждого значения объёма выборки <tex>n</tex>, так и образовываться путём добавления одного элемента к уже имеющейся выборке объёма <tex>n-1</tex>. По результатам расчётов необходимо построить следующие графики:
+Необходимо провести исследование одного или нескольких классических критериев проверки статистических гипотез. Интерес представляет поведение
+[[Достигаемый уровень значимости|достигаемого уровня значимости]] (p-value) как функции размера выборок и параметров распределения. В соответствии с индивидуальными параметрами задания необходимо указанным способом сгенерировать одну или несколько выборок из заданного распределения, выполнить [[Проверка статистических гипотез|проверку гипотезы]] при помощи соответствующего критерия, а затем многократно повторить эту процедуру для различных значений параметров. По результатам расчётов необходимо построить требуемые в задании графики, среди которых могут быть следующие:
-* график зависимости достигаемого уровня значимости от значений параметров при однократном проведении эксперимента;
+# график зависимости достигаемого уровня значимости от значений параметров при однократном проведении эксперимента;
-* график зависимости достигаемого уровня значимости от значений параметров, усреднённого по нескольким десяткам экспериментов;
+# график зависимости достигаемого уровня значимости от значений параметров, усреднённого по большому количеству повторений эксперимента (например, по 100, 500, 1000 повторений);
-* график с эмпирическими оценками [[Мощность критерия|мощности критерия]] для разных значений параметров.
+# график с эмпирическими оценками [[Мощность критерия|мощности критерия]] для разных значений параметров.
 В качестве оценки мощности принимается доля отвержений нулевой гипотезы среди всех проверок. То есть, если эксперимент повторялся <tex>k</tex> раз для каждого набора значений параметра, и в <tex>m</tex> из <tex>k</tex> случаев гипотеза была отвергнута на некотором фиксированном уровне значимости <tex>\alpha</tex> (примем <tex>\alpha=0.05</tex>), оценкой мощности будет отношение <tex>m/k</tex>.
-Необходимо сдать: выполненный в LaTex или Microsoft Word отчёт с описанием алгоритма, построенными графиками и '''выводами (объяснение полученных результатов моделирования, границы применимости критерия и т.д.)''', а также *.m-файл.
+Необходимо сдать: выполненный в LaTex или Microsoft Word отчёт с описанием алгоритма, построенными графиками и '''выводами (объяснение полученных результатов моделирования, границы применимости критерия и т.д.)''', а также *.m-файл, при запуске которого на экран выводятся графики, соответствующие имеющимся в отчёте (допускается, хотя и не рекомендуется использование среды R).
+Задание принимается до '''первого ноября.'''
+== Пример задания ==
+Исследуем поведение классического двухвыборочного [[Критерий Стьюдента|критерия Стьюдента]] для проверки гипотезы однородности против [[Гипотеза сдвига|альтернативы сдвига]] при разных значениях параметров.
-== Пример выполнения задания ==
-Исследуем поведение классического двухвыборочного [[Критерий Стьюдента|критерия Стьюдента]] для проверки гипотезы однородности против [[Гипотеза сдвига|альтернативы сдвига]].
 <tex>x^n = (x_1,\ldots,x_n)\sim N(\mu_1,\sigma),\;\; y^n = (y_1,\ldots,y_n)\sim N(\mu_2,\sigma);</tex>
@@ Строка 19: / Строка 23: @@
 <tex>H_1\,:\; \mu_1\neq\mu_2.</tex>
-Параметры задачи принимают следующие значения:
+<tex>\sigma = 1; \;\;\; \mu_1=0; \;\;\; \mu_2=0\,:\,0.05\,:\,3; \;\;\;  n=5\,:\,1\,:\,50.</tex>
-<tex>\sigma = 1; \;\;\; \mu_1=0; \;\;\; \mu_2=0\,:\,0,05\,:\,3; \;\;\;  n=5\,:\,1\,:\,50.</tex>
 При каждом значении <tex>\mu_2</tex> выборки для разных значений <tex>n</tex> генерируются независимо.
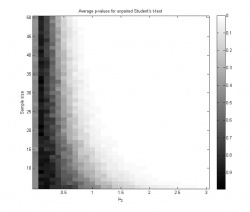
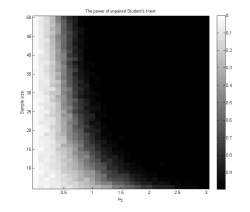
-График значений достигаемого уровня значимости при однократной генерации выборок:
+<gallery widths="250px" heights="250px">
+Изображение:Answer.jpg|График 1: значения достигаемого уровня значимости при однократной генерации выборок.
+Изображение:Answer2.jpg|График 2: значения достигаемого уровня значимости, усрёднённые по 100 экспериментам.
+Изображение:Answer3.jpg|График 3: значения эмпирических оценок мощности критерия при проведении 100 экспериментов (<tex>\alpha=0.05</tex>).
+</gallery>
+== Задания==
+=== Анализ устойчивости критериев к нарушению предположений ===
+* Исследовать устойчивость одновыборочного [[Критерий Стьюдента|критерия Стьюдента]] к нарушению предположения о нормальности данных. <tex>x^n</tex>&nbsp;— смесь распределений <tex>N(\mu,1)</tex> и <tex>U[-a+\mu,a+\mu]</tex> с весами <tex>p</tex> и <tex>1-p</tex> соответственно (при генерации выборки используется случайный датчик&nbsp;— если его значение не превосходит <tex>p</tex>, то добавляем в выборку элемент, взятый из нормального распределения, иначе&nbsp;— элемент, взятый из равномерного). Для разных значений параметров выборки генерируются независимо. <br> <tex>H_0\,:\; \mu=0, \;\; H_1\,:\; \mu\neq 0;</tex> <br> <tex>p=0\,:\,0.02\,:\,1; \;\;  \mu=-1\,:\,0.05\,:\,1; \;\; n=100.</tex> <br> Построить графики вида 1, 2, 3, сделать выводы о чувствительности критерия к зашумлению выборки.
+::Студент 1: <tex>a=1.</tex>
+::Студент 2: <tex>a=5.</tex>
+::Студент 3: <tex>a=10.</tex>
+* Исследовать устойчивость двухвыборочного [[Критерий Стьюдента|критерия Стьюдента]] для независимых выборок к нарушению предположения о нормальности данных. <tex>x^n \sim N(\mu_1,1),</tex> <tex>y^n</tex>&nbsp;— смесь распределений <tex>N(\mu_2,1)</tex> и <tex>U[-a+\mu_2,a+\mu_2]</tex> с весами <tex>p</tex> и <tex>1-p</tex> соответственно (при генерации выборки используется случайный датчик&nbsp;— если его значение не превосходит <tex>p</tex>, то добавляем в выборку элемент, взятый из нормального распределения, иначе&nbsp;— элемент, взятый из равномерного). Для разных значений параметров выборки генерируются независимо. <br> <tex>H_0\,:\; \mu_1=\mu_2, \;\; H_1\,:\; \mu_1\neq\mu_2;</tex> <br> <tex>\mu_1=0; \;\; p=0\,:\,0.02\,:\,1; \;\;  \mu_2=-1\,:\,0.05\,:\,1; \;\; n=100.</tex> <br> Построить графики вида 1, 2, 3, сделать выводы о чувствительности критерия к зашумлению одной из выборок.
+::Студент 4: <tex>a=1.</tex>
+::Студент 5: <tex>a=5.</tex>
+::Студент 6: <tex>a=10.</tex>
+=== Анализ чувствительности критериев к редактированию выборки===
+* Известно, что исключение из выборки определённых наблюдений зачастую может достаточно сильно повлиять на результат анализа. Необходимо исследовать чувствительность одновыборочного критерия [[Критерий Стьюдента|критерия Стьюдента]] к редактированию выборки. <br> <tex>x^n \sim N(\mu,\sigma);</tex> <br> <tex>H_0\,:\; \mu=0, \;\;\; H_1\,:\; \mu>0.</tex> <br> При каждом значении параметра <tex>\mu</tex> генерируется выборка размера <tex>n</tex>, проводится проверка гипотезы <tex>H_0</tex>, затем по некоторому правилу из выборки исключается один из элементов, проверка гипотезы повторяется, затем исключается ещё один, и&nbsp;т.д. Обозначим за <tex>K</tex> максимальное число исключённых в таком процессе элементов. Построить графики вида 1, 2, 3, сделать выводы о чувствительности критерия к редактированию выборки.
+::Студент 7: <tex>n=100;\;\;K=50;\;\;\sigma=1;\;\;\mu=-1\,:\,0.01\,:\,1;\;\;</tex> на каждом шаге исключается максимальный элемент.
+::Студент 9: <tex>n=200;\;\;K=100;\;\;\sigma=5;\;\;\mu=-2\,:\,0.02\,:\,2;\;\;</tex> на каждом шаге исключается максимальный элемент.
+::Студент 10: <tex>n=100;\;\;K=50;\;\;\sigma=2;\;\;\mu=-2\,:\,0.02\,:\,2;\;\;</tex> на каждом шаге исключается минимальный элемент.
+::Студент 11: <tex>n=200;\;\;K=100;\;\;\sigma=5;\;\;\mu=-3\,:\,0.03\,:\,3;\;\;</tex> на каждом шаге исключается минимальный элемент.
+=== Анализ поведения схожих критериев ===
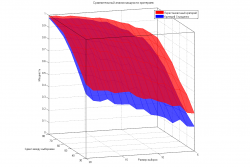
+Требуется исследовать поведение указанной пары статистических критериев, подходящих для решения одной и той же задачи, сравнить мощность и достигаемые уровни значимости и сделать выводы о границах применимости критериев. Необходимо для каждого из критериев построить графики зависимости достигаемых уровней значимости и оценок мощностей от параметров, и показать, в каких областях изменения параметров предпочтительнее использовать тот или иной критерий. Выбрать вид графиков так, чтобы различия между критериями были видны наиболее ясно (например, график вида 4).
+<gallery widths="250px" heights="250px">
+Изображение:Power primer.png|График 4: значения эмпирических оценок мощности критериев при проведении 100 экспериментов.
+</gallery>
+* <tex>x^n \sim N(0,1),\;\;y^n \sim N(\mu,1);</tex> <br> <tex>H_0\,:\; \mu=0, \;\;\; H_1\,:\; \mu\neq 0; </tex> <br> <tex>\mu=-2\,:\,0.02\,:\,2;\;\; n=10\,:\,5\,:\,100.</tex>
+::Студент 12: двухвыборочный [[критерий Стьюдента]] для независимых выборок и [[критерий Уилкоксона-Манна-Уитни]].
+::Студент 13: двухвыборочный [[критерий Стьюдента]] для связных выборок и [[критерий Уилкоксона для связных выборок]].
+::Студент 14: двухвыборочные [[критерий Стьюдента]] для связных и независимых выборок.
+::Студент 15: [[критерий Уилкоксона-Манна-Уитни]] и [[медианный критерий]].
+::Студент 16: [[критерий Уилкоксона для связных выборок]] и [[критерий знаков]].
+::Студент 8: [[критерий знаков]] и [[медианный критерий]].
+* <tex>x^n \sim Be(p_1),\;\;y^n \sim Be(p_2);</tex> <br> <tex>a = \sum_{n}I\(x_i=1\),\;\;  b = \sum_{n}I\(x_i=0\),\;\; c = \sum_{n}I\(y_i=1\),\;\;  d = \sum_{n}I\(y_i=0\);</tex> <br> <tex>  H_0\,:</tex> связь между признаками в [[Таблица сопряженности|таблице сопряжённости]] 2×2, задаваемой величинами <tex>a, b, c, d,</tex> отсутствует; <tex>\;\;\; H_1\,:</tex> признаки связаны между собой.
+::Студент 17: [[Таблица сопряженности#Критерий "хи-квадрат" для анализа таблиц сопряженности|критерий хи-квадрат]] и [[Точный тест Фишера|точный критерий Фишера]]. <tex>p_1=0\,:\,0.02\,:\,1; \;\; p_2=0\,:\,0.02\,:\,1; \;\;n=50.</tex>
+[[Категория:Учебные курсы]]
+::Студент 18: [[Таблица сопряженности#Критерий "хи-квадрат" для анализа таблиц сопряженности|критерий хи-квадрат]] и [[Точный тест Фишера|точный критерий Фишера]]. <tex>p_1=0.5; \;\; p_2=0\,:\,0.05\,:\,1; \;\;n=10\,:\,2\,:\,50.</tex>
+* <tex>x^n</tex> &nbsp;— смесь распределений <tex>N(0,1)</tex> и <tex>U[-a,a]</tex> с весами <tex>p</tex> и <tex>1-p</tex> соответственно (при генерации выборки используется случайный датчик&nbsp;— если его значение не превосходит <tex>p</tex>, то добавляем в выборку элемент, взятый из нормального распределения, иначе&nbsp;— элемент, взятый из равномерного). <br> <tex> H_0\,:\; x \sim N(0,1), \;\;\; H_1\,:\; H_0 </tex> неверна; <br> <tex>p=0\,:\,0.02\,:\,1; \;\; n=10\,:\,5\,:\,100.</tex>
+::Студент 19: [[критерий Шапиро-Уилка]] и [[критерий Колмогорова-Смирнова]]. <tex>a=1.</tex>
+::Студент 20: [[критерий омега-квадрат]] и [[критерий Шапиро-Уилка]]. <tex>a=2.</tex>
+::Студент 21: [[критерий хи-квадрат]] и [[критерий омега-квадрат]]. <tex>a=5.</tex>
+::Студент 22: [[критерий Колмогорова-Смирнова]] и [[критерий хи-квадрат]]. <tex>a=7.</tex>
+= Задание 2. Анализ реальных данных  =
+Ниже приведены описания анализируемых данных и постановки задач. Сами данные каждый студент может получить по электронной почте сразу после сдачи первого задания. При проведении анализа можно пользоваться любыми доступными программными средствами. Необходимо предоставить подробный письменный отчёт по проведённому исследованию, содержащий выводы и описания каждого этапа анализа&nbsp;— используемые методы, обоснование их применимости, промежуточные результаты вычислений, графики. Помимо выводов, касающихся математических особенностей решения, необходимо включить в отчёт заключения, сформулированные в терминах предметной области, которые могли бы быть понятны гипотетическому заказчику-нематематику.
+Задание принимается с 1 по 20 декабря. Напоминаю, что сдача задания является необходимым условием получения допуска к экзамену&nbsp;—  студенты, не получившие зачёт по второму заданию к моменту сдачи экзамена, не смогут его сдавать, и должны будут выполнить задание к пересдаче. Среди студентов, сдающих задание после 20 декабря, проводится конкурс: последние трое сдавших зачёт получат на экзамене дополнительный билет, основанный на материалах курса, но не входящий в основной список вопросов.
+=== Летальность пациентов с сепсисом ===
+По 454 пациентам с сепсисом (лихорадка, тахикардия, тахипноэ и острая недостаточность по крайней мере одной системы органов) имеются следующие данные: оценка начального состояния по шкале APACHE острых и хронических функциональных изменений, факт наступления смерти в течение 30 дней после начала исследования (для каждого значения APACHE score приведены общее число пациентов в таком состоянии и соответствующее число пациентов, умерших в течение 30 дней).
+::Студент 7: оценить вероятность наступления в 30-дневный срок летального исхода в зависимости от исходного состояния. Построить функции, дающие точечную оценку и границы 95% доверительного интервала.
+=== Линейные размеры тысячефранковых банкнот ===
+[[Изображение:CHF1000 2 back horizontal.jpg|300px|thumb|Банкнота в 1000 швейцарских франков серии, действовавшей в период с 1911 по 1958. Красным обозначены измеренные величины.]]
+Имеются данные измерений двухсот швейцарских тысячефранковых банкнот, бывших в обращении в первой половине XX века. Сто из банкнот были настоящими, а сто - поддельными. Измерены следующие величины:  <tex>X_1</tex>&nbsp;— длина банкноты, <tex>X_2</tex>&nbsp;—ширина банкноты с левой стороны, <tex>X_3</tex>&nbsp;—ширина банкноты с правой стороны, <tex>X_4</tex>&nbsp;—расстояние от нижнего края до рамки рисунка, <tex>X_5</tex>&nbsp;— расстояние от нижнего края до рамки рисунка, <tex>X_6</tex>&nbsp;— длина диагонали рисунка.
+::Студент 12: построить функцию, оценивающую по данным измерений вероятность того, что имеющаяся банкнота фальшивая, и 95% доверительный интервал для этой вероятности.
+::Студент 15: построить функции, оценивающие вероятность того, что имеющаяся банкнота фальшивая, по признакам <tex>X_1-X_3</tex> и по признакам <tex>X_4-X_6</tex>. Сравнить эффективность выявления фальшивых купюр по двум группам признаков, сделать выводы.
+=== Ценообразование бриллиантов ===
+Имеются данные о цене и потребительских качествах 308 бриллиантов, продававшихся в Сингапуре в 2000 году. Известны: вес бриллианта в каратах, цвет (закодирован буквами латинского алфавита: наиболее чистый цвет&nbsp;— буквой D, менее чистые&nbsp;— буквами E, F, G и т.д., чем ближе к концу алфавита, тем "грязнее"), группа чистоты (отсутствие дефектов, профессиональная оценка, выдаваемая специалистами при исследовании бриллианта в лупу десятикратного увеличения; бриллианты без трещин и включений получают оценку IF ("internally flawless"), далее в порядке убывания чистоты следуют группы VVS1 и VVS2 ("very very slightly imperfect"), VS1 и VS2 ("very slightly imperfect")), название организации, выдавшей сертификат по группе чистоты (GIA&nbsp;— Gemmological Institute of America, IGI&nbsp;— International Gemmological Institute, HRD&nbsp;— Hoge Raad Voor Diamant), стоимость бриллианта в сингапурских долларах.
+::Студент 13: построить модель ценообразования бриллиантов, учитывая все особенности имеющихся данных.
+::Студент 8: отличается ли средняя цена бриллиантов, сертифицированных различными организациями?
+::Студент 16: какой признак более значимо влияет на цену бриллиантов&nbsp;— цвет или чистота?
+::Студент 14: существует общепринятая система классификации бриллиантов на мелкие&nbsp;— до 0.29 карата, средние&nbsp;— от 0.30 до 0.99 карата и крупные&nbsp;— свыше 1 карата. Достаточно ли для предсказания цены знать о весе бриллианта только к какому классу он относится, или предсказания с использованием знаний о точном весе значимо лучше?
+=== Счета за электроэнергию ===
+Имеются помесячные данные о тратах на электроэнергию одного фиксированного домохозяйства на среднем западе США. За каждый месяц 1991-2000 годов приведены затраты на электроэнергию в долларах. Для объяснения колебаний размера счёта приведены следующие переменные:
+среднемесячная температура по данным последних тридцати лет, погодные индексы CDD и HDD (CDD - Cooling Degree Day - количество градусов, на которые средняя дневная температура больше 65°F, взятое суммой за все дни месяца; HDD - Heating Degree Day - аналогично, суммарное количество градусов, на которое средняя дневная температура меньше 65°F), число проживающих в доме членов семьи, индикатор установки нового счётчика, индикаторы установки двух новых тепловых насосов, объём потребления электроэнергии в киловатт-часах.
+::Студент 2: предсказать объём потребления и затраты на электроэнергию в каждом месяце 2001 года.
+::Студент 9: оценить влияние установки нового оборудования на объём потребления и затраты на электроэнергию.
+::Студент 10: построить функцию, предсказывающую затраты на электроэнергию по температуре, погодным индексам и числу проживающих в доме.
-[[Изображение:Answer.jpg|500px]]
+=== Кассовые сборы кинофильмов ===
+Рассматриваются 428 фильмов с наибольшими кассовыми сборами в истории (по данным boxofficemojo.com). По каждому фильму известны: название, студия, на которой он был снят, суммарные кассовые сборы, сборы в США и в остальном мире по отдельности, год выхода, индикатор повторного выхода картины в прокат.
+::Студент 18: сравнить по всем подходящим признакам фильмы студий Warner Bros., Buena Vista, Universal, Fox, Paramount и Sony (в совокупности ими снято 324 фильма из рассматриваемых 428). Есть ли значимые отличия между продукцией этих студий по какому-либо из признаков?
+::Студент 22: построить функцию, оценивающую сборы фильма за пределами США, по сборам в США, названию студии, году выпуска и индикатору повторного выхода в прокат.
+::Студент 11: есть ли связь между сборами фильма и годом выхода на экраны? Использовав дополнительную информацию о среднегодовой цене билета, привести кассовые сборы рассматриваемых фильмов к ценам 2010 года. Оценить связь между преобразованными сборами фильма и годом выхода на экраны.
-График значений достигаемого уровня значимости, усрёднённых по 100 экспериментам:
+=== Нормальная температура тела ===
+У 130 испытуемых были измерены температура тела и пульс, записаны также данные о поле испытуемых.
+::Студент 6: построить функцию для оценки температуры по пульсу и полу испытуемого.
+::Студент 4: построить функцию для оценки пульса по температуре тела и полу испытуемого.
+:Студент 5: построить функцию, предсказывающую, какого пола испытуемый, на основе результатов измерений пульса и температуры, оценить надёжность такого предсказания.
-[[Изображение:Answer2.jpg|500px]]
+=== Вкус воды ===
+У 106 испытуемых, пришедших на праздник университета Лонгвуд, выяснили, какую воду они обычно пьют - бутилированную, фильтрованную или водопроводную. По каждому из опрошенных имеются также данные о поле, возрасте и предпочитаемой марке бутилированной воды, если такая есть. После опроса испытуемым предложили расставить в порядке ухудшения вкусовых качеств четыре образца воды - марок Fiji, Sam’s Choice, Aquafina и обычную водопроводную воду, причём ни сами испытуемые, ни опрашивающие не знали, какой образец какую воду содержит (двойной слепой тест).
+::Студент 19: исследовать распределение приоритетов по результатам двойного слепого теста, рассмотреть связь между результатами теста и заявленными предпочтениями.
+::Студент 1: отличаются ли мужчины и женщины по заявленным предпочтениям или результатам слепого теста?
+::Студент 21: верно ли, что испытуемые, пьющие бутилированную воду, дают более низкие оценки водопроводной воде, чем все остальные? Верно ли, что те, кто пьёт фильтрованную воду, дают ей более низкие оценки, чем те, кто пьёт водопроводную?
-График значений эмпирических оценок мощности критерия при проведении 100 экспериментов:
+=== Эффективность тромболитической терапии===
+Собраны данные по 206 пациентам второго кардиологического отделения московской городской клинической больницы №25. Имеются результаты 14 анализов, а также 8 дополнительных признаков, описывающих пациента (пол, возраст, курение, наличие диабета и т.д.)
+::Студент 20: построить функцию, оценивающую вероятность выздоровления пациента в результате тромболитической терапии по приведённым 22 признакам.
+::Студент 3: построить функцию, оценивающую вероятность возникновения осложнений у пациента в результате тромболитической терапии по приведённым 22 признакам.
+::Студент 17: оценить влияние курения на вероятности выздоровления и возникновения осложнений, а также на результаты 14 анализов.
-[[Изображение:Answer3.jpg|500px]]
+= Ссылки =
+* [[Статистический анализ данных (курс лекций, К.В.Воронцов)]]
+* [http://www.mathworks.com/help/toolbox/stats/bq_w_hm.html Справка по статистическим функциям пакета Matlab]
+* [[Участник:Riabenko|Контактная информация, необходимая для сдачи задания]]
+[[Категория:Учебные курсы]]