Связанный Байесовский вывод

Материал из MachineLearning.

(Различия между версиями)

Текущая версия

Уильям Оккам — английский философ-схоласт, логик и церковно-политический писатель (ок 1285—1349), автор принципа: «не умножай сущности без необходимости». Этот принцип поддерживается двумя соображениями. Во-первых, эстетическим: «При описании результатов экспериментов у теории с красивой математикой больше шансов на успех, чем у безобразной» — Поль Дирак. Во-вторых, применение бритвы Оккама уже имело большой успех при решении практических задач.

Cвязанный Байесовский вывод — метод сравнения регрессионных моделей основанный на анализе их пространства параметров. Этот метод использует классический Байесовский вывод дважды: для вычисления апостериорной вероятности параметров модели и для вычисления апостериорной вероятности самой модели. Связанность заключается в том, что оба вывода используют общий сомножитель, называемый доcтоверностью модели. Неотъемлемой частью этого метода является анализ пространства параметров модели и зависимости целевой функции от значений параметров. Результатом такого анализа является возможность оценить насколько важны отдельные параметры модели для аппроксимации данных. Cвязанный Байесовский вывод используется как в задачах регрессии, так и в задачах классификации.

Содержание

1 Сравнение моделей
2 Пример вычисления правдоподобия моделей
3 Два уровня Байесовского вывода
4 Пример интепретации множителя Оккама
5 Формула Байеса, кратко
6 Смотри также
7 Литература
8 Внешние ссылки

Сравнение моделей

Правдоподобие двух моделей. Рисунок дает интуитивное представление о том, почему более сложные модели являются менее правдоподобными. Ось абсцисс является предполагаемым пространством данных $D$ .

При сравнении моделей используется правило бритвы Оккама в следующей формулировке: Совместный Байесовский вывод автоматически количественно выполняет правило Оккама. Бритва Оккама — принцип предпочтения простых моделей (теорий, гипотез) сложным. Если несколько моделей одинаково хорошо описывают наблюдения, принцип Оккама рекомнедует выбор простейшей модели.

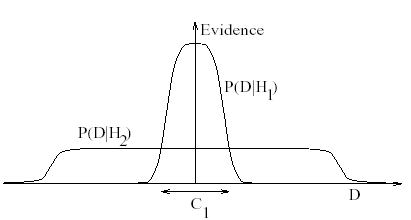
Теорема Байеса говорит о том, что наиболее вероятными будут те модели, которое наиболее точно предсказывают появление некоторых данных. Эта вероятность определяется нормализованной функцией распределения на пространстве данных $D$ . Вероятность $P(D|H_i)$ появления данных $D$ при фиксированной модели $H_i$ называется правдоподобием модели $H_i$ .

Простая модель $H_1$ описывает ограниченное множество данных, что показано на рисунке функцией плотности распределения $P(D|H_1)$ . Более сложная модель $H_2$ , имеющая, например, большее количество параметров, описывает (иначе говоря, приближает с некоторой точностью, не хуже заданной) большее множество данных. Это, согласно нормированию функции плотности распределения, означает, что в некоторой области $C_1$ простая модель $H_1$ будет более вероятной при условии, что обе модели имеют одинаковую априорную вероятность.

Найдем правдоподобие двух альтернативных моделей $H_1$ и $H_2$ , описывающих данные $D$ . По теореме Байеса мы связываем правдоподобие P $(H_1|D)$ модели $H_1$ при фиксированных данных, вероятность $P(D|H_1)$ получения данных с этой моделью и априорное правдоподобие $P(H_1)$ модели $H_1$ . Так как значение нормирующего множителя $P(D)={\sum\limits_{j=1}^nP(D|H_j)P(H_j)}$ для обеих моделей одинаково, то отношение правдоподобия моделей $H_1$ и $H_2$ имеет вид

$\frac{P(H_1|D)}{P(H_2|D)}=\frac{P(H_1)P(D|H_1)}{P(H_2)P(D|H_2)}.$ (1)

Отношение $\frac{P(H_1)}{P(H_2)}$ в правой части указывает на то, насколько велико априорное предпочтение модели $P(H_1)$ модели $P(H_2)$ . Отношение $\frac{P(D|H_1)}{P(D|H_2)}$ указывает насколько модель $H_1$ соответствует наблюдаемым данным лучше, чем модель $H_2$ .

Выражение (1) вводит правило Оккама следующим образом. Во-первых, возможно задать отношение $\frac{P(H_1)}{P(H_2)}$ так, чтобы оно отражало сложность моделей на основании некоторой дополнительной информации. Во-вторых, независимо от предыдущего способа задания критерия отбора моделей, это отношение автоматически выполняет правило Оккама. Действительно, если $H_2$ — более сложная модель, ее плотность распределения $P(D|H_2)$ имеет меньшие значения, при том условии, что ее дисперсия больше. Если невязки, доставляемые обеими моделями равны, простая модель $H_1$ будет более вероятна, чем сложная модель $H_2$ . Таким образом, независимо от априорных предпочтений, вводится правило Оккама, согласно которому при равных априорных предпочтениях и равном соответствии предполагаемых моделей измеряемым данным, простая модель более вероятна, чем сложная.

Пример вычисления правдоподобия моделей

Рассмотрим последовательность $-1,3,7,11.$ Требуется предсказать следующие два числа и найти закономерность последовательности. Первый вариант: $15,19$ . Закономерность $H_a$ есть последующее число есть предыдущее плюс $4$ , иначе $x_{i+1}=x_i+4$ . Второй вариант: $-19.9,1043.8$ . Закономерность $H_c$ есть $x_{i+1}=-x_i^3/11+9/11x_i^2+23/11$ .

С одной стороны, возможно непосредственно назначить априорные вероятности для обеих моделей так, чтобы штрафовать более сложную модель. С другой стороны, возможно вычислить их правдоподобие, $P(D|H_a)$ и $P(D|H_c)$ чтобы определить, насколько хорошо обе функции описывают данные.

Модель $H_a$ зависит от двух параметров: добавляемого числа $n$ и от первого числа в последовательности. Пусть каждый из этих параметров принадлежит множеству $\{-50,\ldots,50\}\supset\mathbb{Z}$ . Так как только пара значений $(n=4, x_1=-1)$ доставляют функцию, соответствующую данным $D=\{-1,3,7,11\}$ , то вероятность появления данных $D$ при заданной модели $H_a$ равна

$P(D|H_a)=\frac{1}{101}\frac{1}{101}=0.00010.$

Для того, чтобы вычислить $P(D|H_c)$ , требуется вычислить вероятность параметров $c, d,e$ в кубическом многочлене $H_c$ .

Эти параметры представлены с виде рациональных чисел (в противном случае обе эти модели были бы несравнимы). Пусть числители параметров, так же как и в предыдущем случае, принимают значения из множества $\{-50,\ldots,50\}$ а знаменатели — из множества $\{1,\ldots,50\}$ . При вычислении вероятности принимается во внимание, что несколько способов представить дробь на заданных множествах. Например, $c=-1/11=-2/22=-3/33=-4/44$ . Вероятность $P(D|H_c)$ равна

$P(D|H_c)=\left(\frac{1}{101}\right) \left(\frac{4}{101}\frac{1}{50}\right) \left(\frac{4}{101}\frac{1}{50}\right) \left(\frac{2}{101}\frac{1}{50}\right) = 0.0000000000025 = 2.5 \times 10^{-12}.$

Отношение правдоподобия двух моделей (а значит и их апостериорных вероятностей при условии равенства априорных предпочтений), $P(D|H_a)=0.00010$ и $P(D|H_a)=2.5{\times}10^{-12}$ составляет одну сорокамиллионную.

Два уровня Байесовского вывода

Использование Байесовского вывода при создании моделей Первый и второй уровень вывода обведены двойной линией.

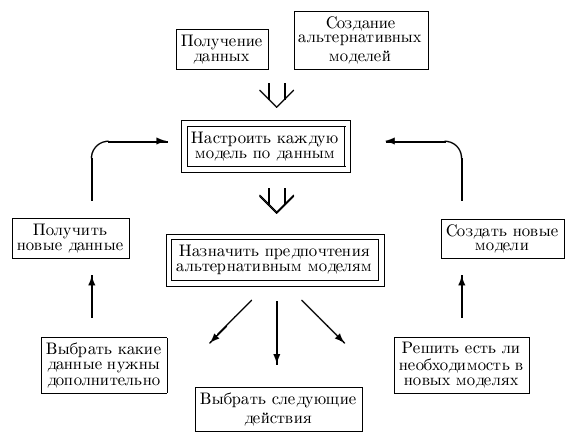
При создании моделей различают два уровня Байесовского вывода. На первом уровне предполагается, что рассматриваемая модель адекватна. Производится настройка параметров модели по данным. В результате получаются наиболее правдоподобные значения параметров и значения ошибок моделей при этих параметрах. Эта процедура повторяется для каждой модели. Задача, решаемая на втором уровне вывода — сравнение моделей. Результатом является упорядоченное множество моделей.

Каждая модель $H_i$ имеет вектор параметров $\mathbf{w}$ . Задача первого уровня — получить оценку параметров $\mathbf{w}$ модели при полученных данных $D$ . Согласно теореме Байеса, апостериорная вероятность параметров $\mathbf{w}$ равна

$P(\mathbf{w}|D,H_i) = \frac{P(D|\mathbf{w},H_i)P(\mathbf{w}|H_i)}{P(D|H_i)},$ (2)

Нормирующая константа $P(D|H_i)$ обычно не принимается во внимание на первом уровне вывода. Однако она становится весьма важной на втором уровне вывода. Эта константа называется в англоязычной литературе evidenve то есть достоверность модели.

При отыскании параметров на практике обычно применяют оптимизационные методы типа алгоритма Левенберга-Марквардта, чтобы получить наиболее вероятные параметры $\mathbf{w}_{MP}$ . (Различают наиболее вероятные параметры $\mathbf{w}_{MP}$ , которые выводятся на первом уровне как аргумент функции вероятности, и наиболее правдоподобные параметры $\mathbf{w}_{ML}$ , которые отыскиваются как аргумент функции наибольшего правдоподобия.)

Ошибка (иногда называемая прогностической способностью) модели $H$ оценивается с помощью функции апостериорного распределения параметров модели. Для оценки используется приближение рядом Тейлора логарифма апостериорного распределения функции $P(\mathbf{w}|D, H_i)$

$P(\mathbf{w}|D,H_i){\approx}P(\mathbf{w}_{MP}|D,H_i)\exp(-\frac{1}{2}\Delta\mathbf{w}^TA\Delta\mathbf{w})),$

где $\Delta\mathbf{w}=\mathbf{w}-\mathbf{w}_{MP}$ , и отыскивается значение гессиана при значении весов максимального правдоподобия $\mathbf{w}_{\tiny\mbox{MP}}$ в окресности $\mathbf{w}_{MP}$ :

$A=-\nabla^2{\ln}P(\mathbf{w}|D,H_i)|_{\mathbf{w}_{MP}}.$

Таким образом, функция апостериорного распределения параметров модели $H_i$ может быть локально приближена с помощью матрицы $A^{-1}$ , которая является матрицей ковариации в окресности значения ее параметров $\mathbf{w}_{MP}$ .

На втором уровне байесовского вывода требуется определить, какая модель наиболее адекватно описывает данные. Апостериорная вероятность $i$ -й модели задана как

$P(H_i|D){\propto}P(D|H_i)P(H_i).$ (2)

Следует отметить, что сомножитель $P(D|H_i)$ , включающий данные $D$ , есть достоверность модели $H_i$ , которая была названа ранее, в выражении (2), нормирующей константой. Достоверность модели может быть получено интегрированием функции правдоподобия по всему пространству параметров модели

$P(D|H_i)={\int}P(D|\mathbf{w},H_i)P(\mathbf{w}|H_i)d\mathbf{w}.$

Второй сомножитель $P(H_i)$ — априорная вероятность над пространством моделей, определяет, насколько адекватной (cоответствующий английский термин — plausible) является модель до того, как появились данные. Основной проблемой Байесовского вывода является отсутствие объективных методов назначения априорной вероятности $P(H_i)$ . Путь априорные вероятности $P(H_i)$ всех моделей равны. Тогда модели ранжируются по значениям достоверности $P(D|H_i)$ .

Чрезвычайно важное предположение, которое необходимо сделать для решения задачи вычисления правдоподобия, — предположение о том, что распределение $P(\mathbf{w}|D,H_i){\propto}P(D|\mathbf{w},H_i)P(\mathbf{w}|H_i)$ имеет выраженный пик в окрестности наиболее вероятного значения $\mathbf{w}_{MP}$ .

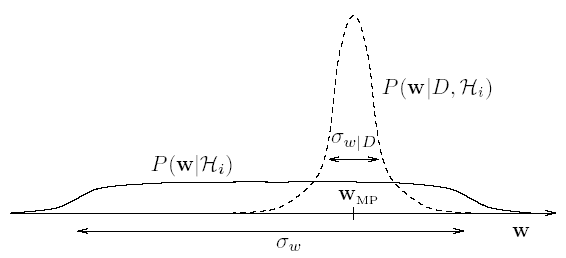
Множитель Оккама — отношение $\sigma_{w|D} P(\mathbf{w}_{MP}|H_i) = \frac{\sigma_{w|D}}{\sigma_{w}}$ }

На рисунке показано, как вычисляется множитель Оккама для модели $H_i$ с единственным параметром $\mathbf{w}$ на оси абсцисс. Сплошной линией показано априорное распределение параметра с дисперсией $\sigma_{w}$ . Апостериорное распределение показано пунктирной линией имеет единственный максимум в точке $\mathbf{w}_{MP}$ и имеет дисперсию $\sigma_{w|D}$ .

Функцию распределения вероятности параметров модели приближают гауссианой, определенной в пространстве параметров. Для этого используется Аппроксимация Лапласа. Согласно этому методу, эта функция равна высоте пика подынтегрального выражения $P(D|\mathbf{w},H_i)P(\mathbf{w}|H_i)$ умноженной на ширину пика, $\sigma_{w|D}$ .

$P(D|H_i)\approx P(D|\mathbf{w}_{MP},H_i) P(\mathbf{w}_{MP}|H_i) \times \sigma_{w|D},$ достоверность $\approx$ наибольшее правдоподобие $\times$ множитель Оккама.

Таким образом, достоверность модели находится с помощью оценок наибольшего правдоподобия параметров модели и множителя Оккама, принимающего значения на отрезке $[0,1]$ , который штрафует модель $H_i$ за ее параметры $\mathbf{w}$ . Чем точнее была априорная оценка параметров, тем меньше штраф.

При аппроксимации Лапласа множитель Оккама может быть получен с помощью определителя ковариационной матрицы весов

$P(D|H_i)\approx P(D|\mathbf{w}_{MP},H_i) P(\mathbf{w}_{MP}|H_i) {\det}^{-\frac{1}{2}} (\mathbf{A}/2\pi),$

где $\mathbf{A}=-\nabla^2{\ln}P(\mathbf{w}|D,H_i)$ — гессиан ковариационной матрицы весов, вычисленный в точке $\mathbf{w}_{MP}$ . Аглоритмически, Байесовский метод сравнения моделей посредством вычисления достоверности не сложнее, чем задача настройки параметров каждой модели и оценки матрицы Гессе.

Итак, для того, чтобы отранжировать альтернативные модели $H_i$ по предпочтению, необходимо, воспользовавшись Байесовским выводом, вычислить достоверность $P(D|H_i)$ . Байесовское сравнение моделей — это расширение метода выбора моделей по методу наибольшего правдоподобия. Достоверность возможно вычислить как для параметрических, так и для непараметических моделей.

Пример интепретации множителя Оккама

Пространство данных и пространство параметров трех модели различной сложности

Переменная $\sigma_{w|D}$ является апостериорной неопределенностью вектора параметров $\mathbf{w}$ . Пусть априорное распределение $P(\mathbf{w}|H_i)$ является равномерным на некотором большом интервале $\sigma_w$ и отражает множество значений, которые были возможны априори, согласно модели $H_i$ . Тогда $P(\mathbf{w}_{MP}|H_i)=1/\sigma_w$ и

множитель Оккама $= \frac{\sigma_{w|D}}{\sigma_{w}}.$

Множитель Оккама есть степень сжатия пространства параметров модели при появлении данных. Модель $H_i$ может быть представлена семейство параметрических функций, из которых фиксируется одна, как только появляются данные. Множитель есть число, обратное количеству таких функций (для конечного их числа). Логарифм множителя Оккама есть мера количества информации о параметрах модели, которая будет получена при появлении данных.

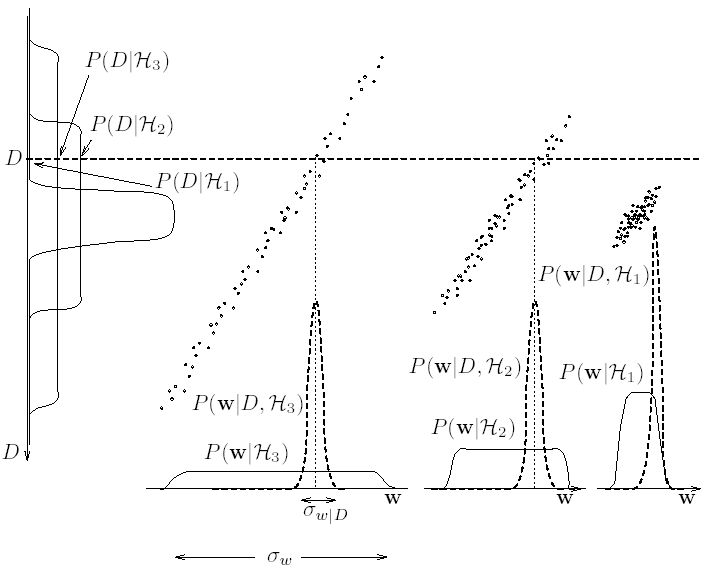
На рисунке показаны три модели, $H_1, H_2$ и $H_3$ , которые имеют равные априорные вероятности. Каждая модель имеет один параметр $\mathbf{w}$ (показан на осях абсцисс), причем параметрам назначены различные априорные области определения $\sigma_W$ . Модель $H_3$ — наиболее «гибкая», или «сложная», с наибольшей априорной областью определения. Одномерное пространство данных показано на оси ординат. Для каждой модели назначено совместное распределение вероятности $P(D,\mathbf{w}|H_i)$ для данных и для параметров. Распределение показано облаками точек — случайных значений этой функции. Число точек для каждой из трех моделей одинаково, так как моделям были назначены одинаковые априорные вероятности.

Когда приходят набор данных $D$ (в данном примере это одна единственная точка на оси ординат), выводится апостериорное распределение параметров моделей. Апостериорное распределение $P(\mathbf{w}|D,H_i)$ показано пунктирной линией внизу. Сплошной линией показано априорное распределение параметров $P(\mathbf{w}|H_3)$ .

Для набора данных $D$ , показанных пунктирной горизонтальной линией, достоверность $P(D|H_3)$ наиболее гибкой модели $H_3$ имеет меньшее значение, чем достоверность модели $H_2$ . Это происходит из-за того, что модель $H_3$ имеет меньшую область пересечения распределения вероятности $P(D,\mathbf{w}|H_i)$ с линиией $D$ , чем модель $H_2$ . В терминах распределения параметров, модель $H_3$ имеет меньшую достоверность, так как множитель Оккама $\sigma_{w|D}/\sigma_{w}$ для модели $H_3$ меньше, чем для модели $H_2$ . Самая простая модель $H_1$ имеет самую малую достоверность, так как хуже всего приближает данные $D$ . Модель $H_3$ слишком универсальна, ее множитель Оккама — штраф за универсальность модели — велик и поэтому она не является лучшей. Для полученного набора данных наиболее вероятна модель $H_2$ .

Формула Байеса, кратко

Условная вероятность $P(D|H)$ есть вероятность события $D$ при условии наступления события $H$ . Из всех элементов множества $\Omega$ элементарных событий, принадлежащих $H$ входят в $D$ лишь те события, которые принадлежат пересечению $H$ и $D$ . Эти элементы определяют $P(D|H)$ . Но, если бы $H$ было нормировано, то $P(D|H)$ равнялось бы $P(HD)$ . Поэтому, чтобы условная вероятность отвечала условиям нормировки, используют нормирующий множитель:

$P(D|H)=\frac{P(HD)}{P(H)}.$

Согласно формуле умножения вероятностей, числитель этой дроби равен

$P(HD)=P(D|H)P(H).$

Разбиение множества $\Omega$ на полную группу несовместимых событий $H_1,\dots,H_n$ позволяет любое событие $D$ записать в виде

$D=DH_1+\dots+DH_n,$

откуда

$P(D)=P(D|H_1)P(H_1)+\dots+P(D|H_n)P(H_n)$ (3)

Пусть $P(H),P(D)>0$ . Тогда из

$P(HD)=P(H|D)P(D)=P(D|H)P(H)$

вытекает

$P(H|D)=\frac{P(D|H)P(H)}{P(D)},$

что после учета (3) при водит к формуле Байеса

$P(H_i|D)=\frac{P(D|H_i)P(H_i)}{\sum\limits_{j=1}^nP(D|H_j)P(H_j)}.$

Смотри также

Литература

Bishop, C. M., Tipping, M. E. Bayesian regression and classification / Suykens, J., Horvath, G. et al., eds. Advances in Learning Theory: Methods, Models and Applications, Vol. 190. IOS Press, NATO Science Series III: Computer and Systems Sciences. 2000. P 267—285.
Bishop, C. Pattern Recognition And Machine Learning. Springer. 2006.
LeCun, Y., Denker, J. S., Solla, S. A. Optimal brain damage / Touretzky, D. S., ed. Advances in Neural Information Processing Systems. Morgan Kaufmann. 1990. P. 598—605.
MacKay, D. Information, inference, learning algorithms. Cambridge University Press. 2003.
MacKay, D. Hyperparameters: optimise or integrate out? / Heidberger, G., ed. Maximum entropy and Bayesian Methods. Santa Barbara, Dordrecht: Kluwer. 1993.
MacKay, D. Choice of basis for Laplace approximation / Machine Learning, vol. 33(1), 1998.
MacKay, D. Bayesian interpolation / Neural Computation 4(3). 1992. P. 415—447.
MakKay, D. Hyperparameters: optimize, or integrate out? Neural Computation. 1999.
Nabney, Yan T., Netlab: Algorithms for pattern recognition. Springer. 2004.
Grunwald, P D., Myung, I. J. (eds.) Advances In Minimum Description Length: Theory And Applications. Springer. 2005.
Burnham, K., Anderson, D. R. Model Selection and Multimodel Inference. Springer. 2002.
Стрижов В. В. Методы индуктивного порождения регрессионных моделей. М.: ВЦ РАН. 2008. 55 с. Брошюра, PDF.
Стрижов В.В., Крымова Е.А. Методы выбора регрессионных моделей. М.: ВЦ РАН, 2010. 60 с. Брошюра, PDF.

Внешние ссылки

Источник — «http://poligon.machinelearning.ru/wiki/index.php?title=%D0%A1%D0%B2%D1%8F%D0%B7%D0%B0%D0%BD%D0%BD%D1%8B%D0%B9_%D0%91%D0%B0%D0%B9%D0%B5%D1%81%D0%BE%D0%B2%D1%81%D0%BA%D0%B8%D0%B9_%D0%B2%D1%8B%D0%B2%D0%BE%D0%B4»

Категории: Регрессионный анализ | Байесовские методы | Энциклопедия анализа данных

@@ Строка 31: / Строка 31: @@
 По теореме Байеса мы связываем правдоподобие&nbsp;P<tex>(H_1|D)</tex> модели&nbsp;<tex>H_1</tex> при фиксированных данных,
 вероятность&nbsp;<tex>P(D|H_1)</tex> получения данных с этой моделью и априорное правдоподобие&nbsp;<tex>P(H_1)</tex> модели&nbsp;<tex>H_1</tex>.
-Так как значение нормирующего множителя&nbsp;<tex>P(D)={\sum\limits_{j=1}^nP(D|H_j)P(H_j)}</tex> для обоих моделей одинаково,
+Так как значение нормирующего множителя&nbsp;<tex>P(D)={\sum\limits_{j=1}^nP(D|H_j)P(H_j)}</tex> для обеих моделей одинаково,
 то отношение правдоподобия моделей&nbsp;<tex>H_1</tex> и&nbsp;<tex>H_2</tex> имеет вид
 <center><tex>\frac{P(H_1|D)}{P(H_2|D)}=\frac{P(H_1)P(D|H_1)}{P(H_2)P(D|H_2)}.</tex> &nbsp;&nbsp;&nbsp;&nbsp;(1)</center>
@@ Строка 49: / Строка 49: @@
 Первый вариант: <tex>15,19</tex>.
 Закономерность&nbsp;<tex>H_a</tex> есть последующее число есть предыдущее плюс&nbsp;<tex>4</tex>, иначе <tex>x_{i+1}=x_i+4</tex>.
-Второй вариант: <tex>-19.9,1043.8</tex>. Закономерность&nbsp;<tex>H_c</tex> есть <tex>x_{i+1}=-x_i³/11+9/11x_i²+23/11</tex>.
+Второй вариант: <tex>-19.9,1043.8</tex>. Закономерность&nbsp;<tex>H_c</tex> есть <tex>x_{i+1}=-x_i^3/11+9/11x_i^2+23/11</tex>.
 С одной стороны, возможно непосредственно назначить априорные вероятности для обеих моделей так, чтобы штрафовать более сложную модель.
@@ Строка 55: / Строка 55: @@
 Модель&nbsp;<tex>H_a</tex> зависит от двух параметров: добавляемого числа&nbsp;<tex>n</tex> и от первого числа в последовательности.
-Пусть каждый из этих параметров принадлежит множеству&nbsp;<tex>\{-50,…,50\}\supset\mathbb{Z}</tex>.
+Пусть каждый из этих параметров принадлежит множеству&nbsp;<tex>\{-50,\ldots,50\}\supset\mathbb{Z}</tex>.
 Так как только пара значений&nbsp;<tex>(n=4, x_1=-1)</tex> доставляют функцию, соответствующую данным <tex>D=\{-1,3,7,11\}</tex>,
 то вероятность появления данных&nbsp;<tex>D</tex> при заданной модели&nbsp;<tex>H_a</tex> равна
@@ Строка 63: / Строка 63: @@
 Эти параметры представлены с виде рациональных чисел (в противном случае обе эти модели были бы несравнимы).
-Пусть числители параметров, так же как и в предыдущем случае, принимают значения из множества&nbsp;<tex>\{-50,…,50\}</tex> а знаменатели&nbsp;— из множества&nbsp;<tex>\{1,…,50\}</tex>.
+Пусть числители параметров, так же как и в предыдущем случае, принимают значения из множества&nbsp;<tex>\{-50,\ldots,50\}</tex> а знаменатели&nbsp;— из множества&nbsp;<tex>\{1,\ldots,50\}</tex>.
 При вычислении вероятности принимается во внимание, что несколько способов представить дробь на заданных множествах.
 Например, <tex>c=-1/11=-2/22=-3/33=-4/44</tex>.
@@ Строка 93: / Строка 93: @@
 важной на втором уровне вывода. Эта константа называется в англоязычной литературе ''evidenve'' то есть ''достоверность модели''.
-При отыскании параметров на практике обычно применяют оптимизационные методы типа [[метод сопряженных градиентов|метода сопряженных градиентов]],
+При отыскании параметров на практике обычно применяют оптимизационные методы типа [[алгоритм Левенберга-Марквардта|алгоритма Левенберга-Марквардта]],
 чтобы получить наиболее вероятные параметры <tex>\mathbf{w}_{MP}</tex>.
-(Различают наиболее вероятные параметры&nbsp;<tex>\mathbf{w}_{MP}</tex> выводятся на первом уровне как аргумент функции вероятности и
+(Различают наиболее вероятные параметры&nbsp;<tex>\mathbf{w}_{MP}</tex>, которые выводятся на первом уровне как аргумент функции вероятности, и
 наиболее правдоподобные параметры&nbsp;<tex>\mathbf{w}_{ML}</tex> , которые отыскиваются как аргумент функции наибольшего правдоподобия.)
@@ Строка 104: / Строка 104: @@
 где <tex>\Delta\mathbf{w}=\mathbf{w}-\mathbf{w}_{MP}</tex>, и отыскивается значение гессиана при значении весов максимального правдоподобия
 <tex>\mathbf{w}_{\tiny\mbox{MP}}</tex> в окресности&nbsp;<tex>\mathbf{w}_{MP}</tex>:
-<center><tex>A=-\nabla²{\ln}P(\mathbf{w}|D,H_i)|_{\mathbf{w}_{MP}}.</tex></center>
+<center><tex>A=-\nabla^2{\ln}P(\mathbf{w}|D,H_i)|_{\mathbf{w}_{MP}}.</tex></center>
 Таким образом, функция апостериорного распределения параметров модели&nbsp;<tex>H_i</tex> может быть локально приближена с помощью матрицы&nbsp;<tex>A^{-1}</tex>,
 которая является матрицей ковариации в окресности значения ее параметров&nbsp;<tex>\mathbf{w}_{MP}</tex>.
@@ Строка 136: / Строка 136: @@
 Функцию распределения вероятности параметров модели приближают гауссианой, определенной в пространстве параметров.
-Для этого используют [[метод Лапласа]].
+Для этого используется [[Аппроксимация Лапласа]].
 Согласно этому методу, эта функция равна высоте пика подынтегрального выражения <tex>P(D|\mathbf{w},H_i)P(\mathbf{w}|H_i)</tex> умноженной на ширину пика, <tex>\sigma_{w|D}</tex>.
@@ Строка 148: / Строка 148: @@
 При аппроксимации Лапласа множитель Оккама может быть получен с помощью определителя ковариационной матрицы весов
 <center><tex> P(D|H_i)\approx P(D|\mathbf{w}_{MP},H_i) P(\mathbf{w}_{MP}|H_i) {\det}^{-\frac{1}{2}} (\mathbf{A}/2\pi),</tex></center>
-где <tex>\mathbf{A}=-\nabla²{\ln}P(\mathbf{w}|D,H_i)</tex>&nbsp;— гессиан ковариационной матрицы весов, вычисленный в точке&nbsp;<tex>\mathbf{w}_{MP}</tex>.
+где <tex>\mathbf{A}=-\nabla^2{\ln}P(\mathbf{w}|D,H_i)</tex>&nbsp;— гессиан ковариационной матрицы весов, вычисленный в точке&nbsp;<tex>\mathbf{w}_{MP}</tex>.
 Аглоритмически, Байесовский метод сравнения моделей посредством вычисления достоверности не сложнее, чем задача настройки параметров каждой модели и оценки матрицы Гессе.
@@ Строка 165: / Строка 165: @@
 Множитель Оккама есть степень сжатия пространства параметров модели при появлении данных.
 Модель&nbsp;<tex>H_i</tex> может быть представлена семейство параметрических функций, из которых фиксируется одна, как только появляются данные.
-Множитель есть число, обратное количеству таких функций (для конечно го их числа).
+Множитель есть число, обратное количеству таких функций (для конечного их числа).
-Логарифм множителя Оккама есть есть мера количества информации о параметрах модели, которая будет получена при появлении данных.
+Логарифм множителя Оккама есть мера количества информации о параметрах модели, которая будет получена при появлении данных.
 На рисунке показаны три модели, <tex>H_1, H_2</tex> и&nbsp;<tex>H_3</tex>, которые имеют равные априорные вероятности.
@@ Строка 196: / Строка 196: @@
 Поэтому, чтобы условная вероятность отвечала условиям нормировки, используют нормирующий множитель:
 <center><tex>P(D|H)=\frac{P(HD)}{P(H)}.</tex></center>
-Согдаснно формуле умножения вероятностей, числитель этой дроби равен
+Согласно формуле умножения вероятностей, числитель этой дроби равен
 <center><tex>P(HD)=P(D|H)P(H).</tex></center>
 Разбиение множества&nbsp;<tex>\Omega</tex> на полную группу несовместимых
@@ Строка 217: / Строка 217: @@
 * [[Гипотеза порождения данных]]
 * [[Метод наибольшего правдоподобия]]
+* [[Аппроксимация Лапласа]]
+* [[Аппроксимация Лапласа (пример)]]
 == Литература ==
@@ Строка 231: / Строка 233: @@
 * {{s|Grunwald, P D., Myung, I. J. (eds.)}} Advances In Minimum Description Length: Theory And Applications. Springer. 2005.
 * {{s|Burnham,&nbsp;K.,  Anderson,&nbsp;D. R.}} Model Selection and Multimodel Inference. Springer. 2002.
+* Стрижов В. В. Методы индуктивного порождения регрессионных моделей. М.: ВЦ РАН. 2008. 55&nbsp;с. [[Media:strijov08ln.pdf|Брошюра, PDF]].
+* Стрижов В.В., Крымова Е.А. Методы выбора регрессионных моделей. М.: ВЦ РАН, 2010. 60&nbsp;с. [[Media:Strijov-Krymova10Model-Selection.pdf|Брошюра, PDF]].
 == Внешние ссылки ==
@@ Строка 239: / Строка 243: @@
 [[Категория:Регрессионный анализ]]
+[[Категория:Байесовские методы]]
 [[Категория:Энциклопедия анализа данных]]