Логистическая регрессия для решения задач классификации (пример)

Материал из MachineLearning.

Версия 10:04, 28 октября 2010

Логистическая регрессия - частный случай обобщенной линейной регрессии. Предполагается, что зависимая переменная принимает два значения и имеет биномиальное распределение.

На практике логистическая регрессия используется для решения задач классификации с линейно-разделяемыми классами.

Постановка задачи восстановления логистической регрессии

Задана выборка - множество  пар , в которых описание -го элемента , и значения зависимой переменной 

Принята модель логистической регрессии, согласно которой свободные переменные  и зависимая переменная  связаны зависимостью

где .

Примем обозначения , вектор  Для удобства дальнейшего изложения обозначим выборку свободных переменных как

Требуется найти такое значение вектора параметров , которое бы доставляло минимум норме вектора невязок

Алгоритм отыскания оптимальных параметров

Оптимальные параметры отыскиваются последовательно с помощью итерационного итерационного взвешенного метода наименьших квадратов (IRLS) с использованием гребневой регрессии для решения проблемы мультиколлинеарности. Приведенный ниже алгоритм основан на алгоритме Ньютона-Рафсона.

В начале работы алгоритма задается начальньное приближение как решение задачи обычным МНК

,

Далее итеративно повторяется следующая процедура.

• С использованием вектора параметров  вычисляется переменная
• Вычисляется восстановленное значение выборки зависимой переменной

• Вычисляется вектор значений зависимой переменной для текущего шага линейной регрессии

 - вектор весов значений зависимой переменной.

• Решается задача наименьших квадратов с взвешиванием элементов выборки и регуляризацией. При этом

больший вес приобретают те элементы, которые имеют большую невязку, и понижается эффективная размерность решения что позволяет работать с плохо обусловленными матрицами.

где диагональная матрица весов .

Процедура останавливается после того, как норма разности векторов параметров на каждой итерации не будет превышать заданную константу: .

Вычислительный эксперимент

Показана работа алгоритма в серии задач, основанных как на реальных, так и на модельных данных.

Пример на реальных данных: Ирисы Фишера

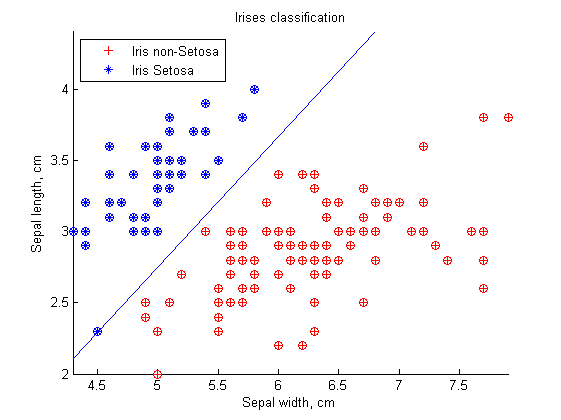
Задача классификации ставится следующим образом: требуется определить принадлежность к классу Цетоза (Setosa) по длине и ширине чашелистника. Данные взяты из файла fisheriris.mat

На графике показаны результаты классификации. По оси абсцисс отложено значение одного признака (длина чашелистника в см.), а по оси ординат — значение второго признака (ширина чашелистникаа в см.). Различные классы показаны крестиками различных цветов, а результат классификации показан кружочками соотвествующего цвета. Пурпурной линией показана граница между классами, построенная алгоритмом.

Алгоритм не допустил ни одной ошибки классификации, поскольку данные линейно разделимы. Это простая задача для любого алгоритма классификации

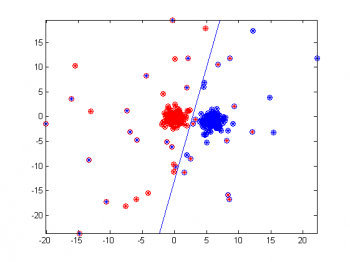
Модельные данные: устойчивость к шумам

Были сгенерированы 2 нормально распределённых линейно разделимых класса. На них наложен шум с большей дисперсией.

%% Create a demonstration data set
N = 100; % 1st class contains N objects
alpha = 1; % 2st class contains alpha*N ones
sig2 = 1; % assume 2nd class has the same variance as the 1st
dist2 = 6;
 
[X, y] = loadModelData(N, alpha, sig2, dist2);
% note that y contains only 1s and 0s
 
% generate noise 10%
NPart = 0.5;
clsNoise = 10 * randn(round(N*NPart), 2);
yN = 2 - randi(2, round(N*NPart), 1);
X = [X; clsNoise];
y = [y; yN];

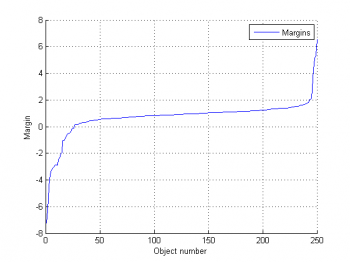
Как видим, данный алгоритм достаточно устойчив к шумам. Классы разделены практически с максимальным зазором. Ошибки наблюдаются только в классификации выбросов. Для наглядности рядом приведен график отступов т.е. расстояния от объекта до разделяющей гипреплоскости. Если отступ отрицателен значит на объекте допущена ошибка классификации.

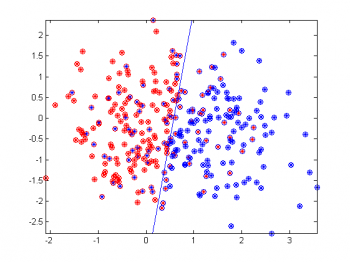
Модельные данные: сильно перекрывающиеся классы

%% Create a demonstration data set
 
N = 150; % 1st class contains N objects
alpha = 1; % 2st class contains alpha*N ones
sig2 = 1; % assume 2nd class has the same variance as the 1st
dist2 = 1;
 
[X, y] = loadModelData(N, alpha, sig2, dist2);
 
%% Plot the initial data
idx1 = find(y == 0); % object indices for the 1st class
idx2 = find(y == 1);
 
h = figure; hold on
plot(X(idx1,1), X(idx1,2), 'r*');
plot(X(idx2,1), X(idx2,2), 'b*');
axis tight
%close(h);
 
%% Training
w = logreglearn(X,y);
 
%% Recovering regression on the same data
p = logregmdl(w,X);
 
%%  Show the result
 
idx1 = find(p > 1/2); % object indices for the 1st class
idx2 = find(p <= 1/2);
% plot the classified data
plot(X(idx1,1), X(idx1,2), 'bo');
plot(X(idx2,1), X(idx2,2), 'ro');
 
% separation hyperplane, formed as a function (here it is a line)
separateXLim = inline( '(-b(1)- YLim*b(3))/b(2)', 'b','YLim');
% plot the hyperplane
plot(separateXLim(w,ylim), ylim, 'b-');

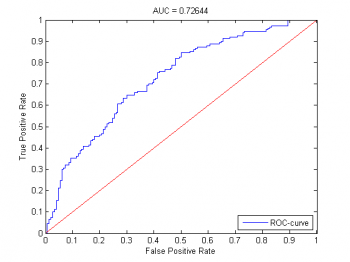
Алгоритм допустил около 30% ошибок классификация, но это и следовало ожидать, т.к. входные данные были принципиально линейно неразделимы. Для этого алгоритма построена ROC-кривая на этих модельных данных.

Исходный код

Скачать листинги алгоритмов можно здесь.

Смотри также

• Логистическая регрессия
• Логистическая регрессия (пример)
• Логистическая функция
• Регрессионный анализ
• Метод наименьших квадратов
• Обобщенная линейная модель
• Алгоритм Ньютона-Рафсона
• Логит-анализ

Литература

• К. В. Воронцов, Лекции по линейным алгоритмам классификации
• Jon E. Anderson "Logistic Regression Model"
• Н. Ибрагимов "Метод максимального правдоподобия" (сс. 78-81, 83-86)

Данная статья была создана в рамках учебного задания. Студент: Данила Дорофеев Преподаватель: В.В. Стрижов Срок: 28 мая 2009 В настоящее время задание завершено и проверено. Данная страница может свободно правиться другими участниками проекта MachineLearning.ru. См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Замечания