Прогнозирование временных рядов методом SSA (пример)

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(→Численный эксперимент)
(→Численный эксперимент)
Строка 83: Строка 83:
Рассмотрим трёхмерный временной ряд, заданный формулами:
Рассмотрим трёхмерный временной ряд, заданный формулами:
-
<tex>$$f_1(t) = 0,08t + 0,9\sin (\frac{2\pi t}{11}) + 0,8\sin (\frac{2\pi (t+0,09)}{8}),$$</tex>
+
<tex>$$f_1(t) = 0,08t + 0,9\sin (\frac{2\pi t}{11}) + 0,8\sin \left(\frac{2\pi (t+0,09)}{8}\right),$$</tex>
<tex>$$f_2(t) = 0,0001t^2 - 0,05t + 0,6\sin (\frac{2\pi (t-0,14)}{11}) + \cos (\frac{2\pi t}{8}),$$</tex>
<tex>$$f_2(t) = 0,0001t^2 - 0,05t + 0,6\sin (\frac{2\pi (t-0,14)}{11}) + \cos (\frac{2\pi t}{8}),$$</tex>

Версия 17:01, 15 июня 2010

SSA (Singular Spectrum Analysis, "Гусеница") - метод анализа и прогноза временных рядов. Базовый вариант метода состоит в:

1) преобразовании одномерного ряда в многомерный с помощью однопараметрической сдвиговой процедуры (отсюда и название "Гусеница");

2) исследовании полученной многомерной траектории с помощью анализа главных компонент (сингулярного разложения);

3) восстановлении (аппроксимации) ряда по выбранным главным компонентам.

Таким образом, результатом применения метода является разложение временного ряда на простые компоненты: медленные тренды, сезонные и другие периодические или колебательные составляющие, а также шумовые компоненты. Полученное разложение может служить основой прогнозирования как самого ряда, так и его отдельных составляющих. "Гусеница" допускает естественное обобщение на многомерные временные ряды, а также на случай анализа изображений. В данной статье рассмотрим вариант алгоритма, предназначенный для анализа многомерного временного ряда.


Содержание

Постановка задачи

Наблюдается система функций дискретного аргумента {$(f_i^{(k)})_{i=1}^N$, где k = 1, ..., s}. s - число временных рядов, k - номер ряда, N - длина временного ряда, i - номер отсчета. Требуется разложить ряд в сумму компонент (используя метод главных компонент, см. описание алгоритма), интерпретировать каждую компоненту, и построить продолжение ряда $(f_i^{(k)})_{i=1}^{N+M}$ по выбранным компонентам.

Описание алгоритма

Построение матрицы наблюдений

Рассмотрим сначала одномерный временной ряд $(f_i)_{i=1}^N.$ Выберем n такое, что $0 < n \le N - 1$ - время жизни многомерной гусеницы. Пусть $\sigma = N - n + 1$ - длина гусеницы. Построим последовательность из n векторов в $R^{\sigma}$ следующего вида:

Y^{(l)} \in R^{\sigma}, Y^{(l)} = (f_{i+l-1})_{i=1}^{\sigma}

Обозначим

$$Z = (Y^{(1)}, \ldots, Y^{(n)}):$$

Изображение:Picture1.jpg


Будем называть $Z$ нецентрированной матрицей наблюдений, порождённой гусеницей со временем жизни n.

В случае многомерного временного ряда матрицей наблюдения называется столбец из матриц наблюдений, соответствующих каждой из компонент.

Проводимый в дальнейшем анализ главных компонент может проводиться как по центрированной, так и по нецентрированной выборкам. Для упрощения выкладок рассмотрим простейший нецентрированный вариант.

Анализ главных компонент

Рассмотрим ковариационную матрицу полученной выборки:

$$C = \frac1n ZZ^T.$$

Выполним её svd-разложение:

$$C = V\Lambda V^T,$$

где $\Lambda = diag(\lambda_1, \ldots, \lambda_{\tau})$ - диагональная матрица собственных чисел, $V = (v^{(1)}, \ldots, v^{(\tau)})$, $(v^{(i)})^T v^{(j)} = \delta_{ij}$ - ортогональная матрица собственных векторов.

Далее рассмотрим систему главных компонент:

$$U = V^T Z, U = (U^{(1)}, \ldots, U^{(\tau)})^T.$$

После проведения анализа главных компонент обычно предполагается проведение операции восстановления исходной матрицы наблюдений по некоторому поднабору главных компонент, т. е. для $V' = (v^{(i_1)}, \ldots, v^{(i_r)})$ и $U' = V'^T Z$ вычисляется матрица $Z' = V'U'$.

Далее восстанавливаются исходные последовательности. В одномерном случае i-ая компонента восстановленного ряда есть среднее значение по i-ой диагонали восстановленной матрицы наблюдений Z':

Изображение:Picture2.jpg

В многомерном случае усреднение проводится с учётом того, что матрица наблюдений состоит из подматриц, соответствующих каждой компоненте ряда:

$$f'_m^{(k)} = \left\{ \begin{array}{ll} \frac1m \sum_{i=1}^m x_i^{(m-i+1,k)}&1\le m\le \sigma,\\ \frac{1}{\sigma} \sum_{i=1}^{\sigma} x_i^{(m-i+1,k)}&\sigma \le m \le n,\\ \frac{1}{N-m+1} \sum_{i=1}^{N-m+1} x_{i+m-n}^{(n-i+1,k)}&n \le m \le N.\end{array} \right$$

Прогноз

Числовой ряд (f_i)_{i=1}^{N+1} называется продолжением ряда (f_i)_{i=1}^N, если порождаемая им при гусеничной обработке выборка лежит в той же гиперплоскости, что и у исходного ряда. Пусть у нас есть некоторый набор выбранных главных компонент i_1, i_2, \ldots, i_r. Определим

$$w = \left ( \begin{array}{cccc} v_{\sigma}^{(i_1)}&v_{\sigma}^{(i_2)}&\ldots&v_{\sigma}^{(i_r)}\\ v_{2\sigma}^{(i_1)}&v_{2\sigma}^{(i_2)}&\ldots&v_{2\sigma}^{(i_r)}\\ \vdots& \vdots &\ddots & \vdots\\ v_{\tau}^{(i_1)}&v_{\tau}^{(i_2)}&\ldots&v_{\tau}^{(i_r)}\end{array} \right ) $$

и

$$ V_* = \left ( \begin{array}{cccc} v_1^{(i_1)}&v_1^{(i_2)}&\ldots&v_1^{(i_r)}\\ \vdots& \vdots &\ddots & \vdots\\ v_{\sigma - 1}^{(i_1)}&v_{\sigma - 1}^{(i_2)}&\ldots&v_{\sigma - 1}^{(i_r)}\\ v_{\sigma + 1}^{(i_1)}&v_{\sigma + 1}^{(i_2)}&\ldots&v_{\sigma + 1}^{(i_r)}\\ \vdots& \vdots &\ddots & \vdots\\ v_{2\sigma - 1}^{(i_1)}&v_{2\sigma - 1}^{(i_2)}&\ldots&v_{2\sigma - 1}^{(i_r)}\\ \vdots& \vdots &\ddots & \vdots\\ v_{\tau - 1}^{(i_1)}&v_{\tau - 1}^{(i_2)}&\ldots&v_{\tau - 1}^{(i_r)}\end{array} \right ) $$

Также положим

$$Q = \left (f_{N-\sigma+2}^{(1)}, \ldots, f_N^{(1)}, f_{N-\sigma+2}^{(2)}, \ldots, f_N^{(2)}, \ldots, f_{N-\sigma+2}^{(s)}, \ldots, f_N^{(s)}\right )^T$$

Тогда прогнозируемые значения системы в точке $N+1$ вычисляются по формуле:

$$f_{N+1} = w(V_*^T V_*)^{-1} V_*^T Q.$$

Численный эксперимент

Модельные данные

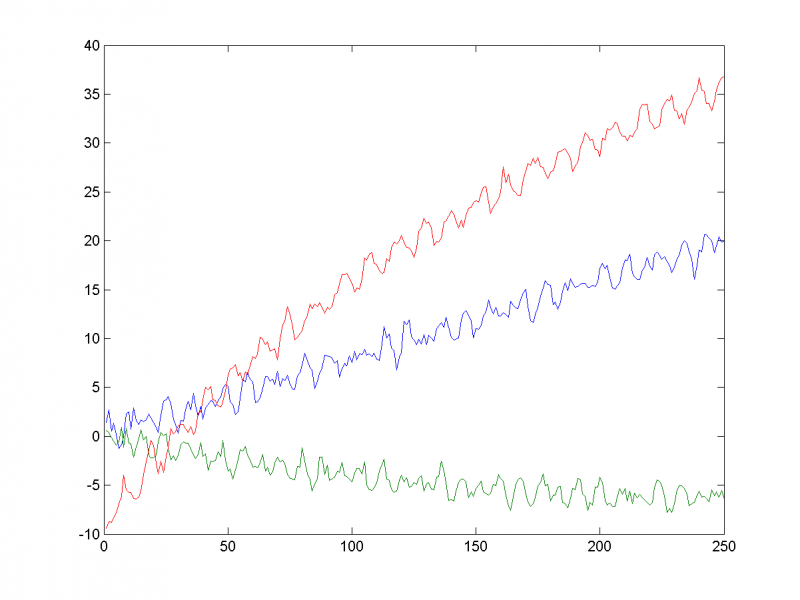
Рассмотрим трёхмерный временной ряд, заданный формулами:

$$f_1(t) = 0,08t + 0,9\sin (\frac{2\pi t}{11}) + 0,8\sin \left(\frac{2\pi (t+0,09)}{8}\right),$$

$$f_2(t) = 0,0001t^2 - 0,05t + 0,6\sin (\frac{2\pi (t-0,14)}{11}) + \cos (\frac{2\pi t}{8}),$$

$$f_3(t) = 36\log(t+100) - 1,2\sin (\frac{2\pi (t+0,24)}{11}) + 0,5\sin (\frac{2\pi (t-0,35)}{8}),$$

где $$t = 1, 2, \ldots, 250$$

Кроме тренда (линейная, квадратичная функции и логарифм соответственно) в ряды добавлены две периодические составляющие (синусоиды с различными амплитудами и фазами). Также во временные ряды добавлен шум со среднеквадратичным отклонением 0,5:

Исследуем главные компоненты данного временного ряда, используя гусеницу длины 50.

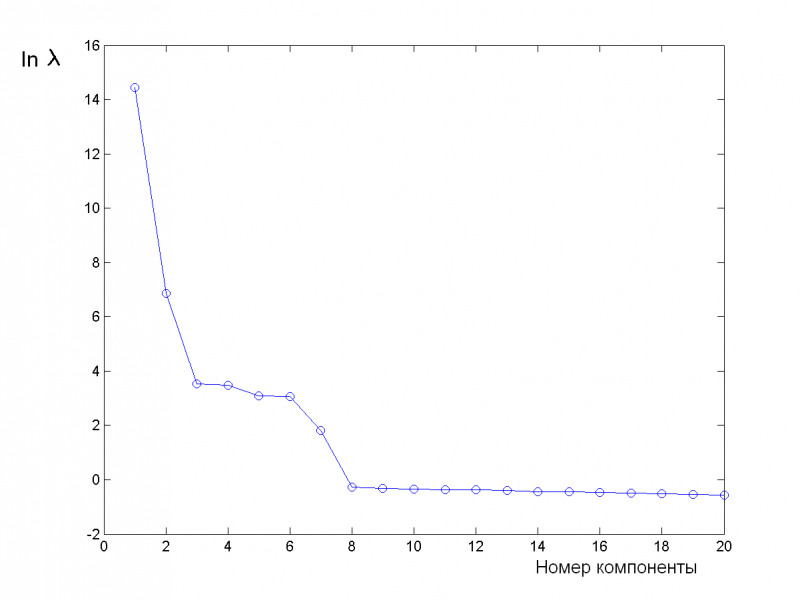
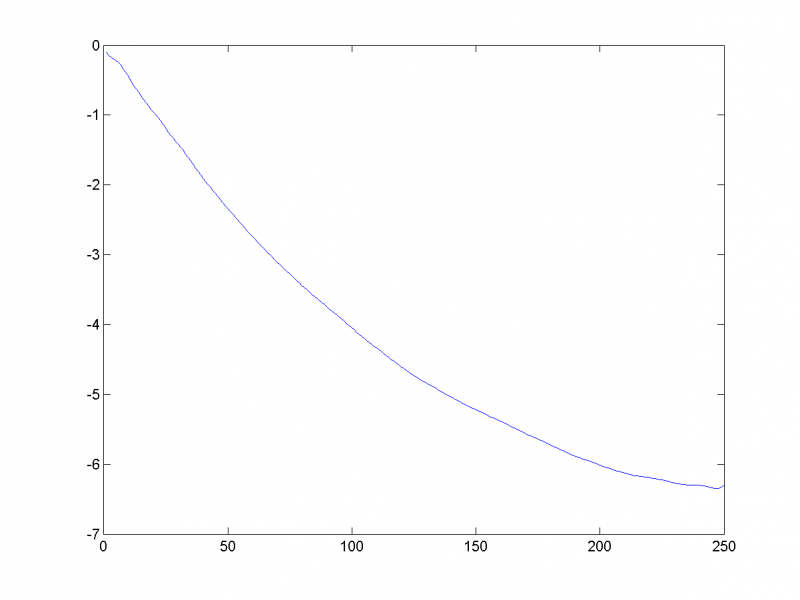
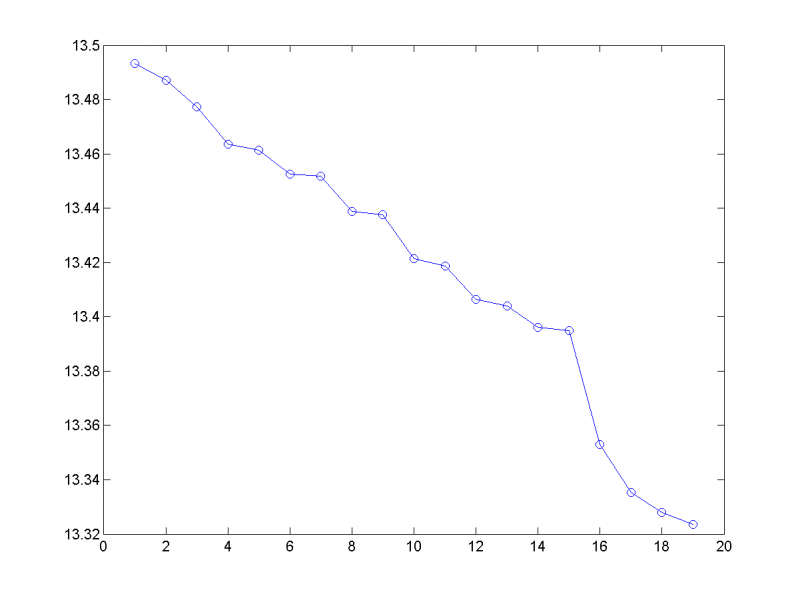
Логарифмы первых двадцати собственных чисел ковариационной матрицы:

Из графика видно, что содержательный смысл несут, вероятно, первые семь главных компонент, а остальные, скорее всего, шум.

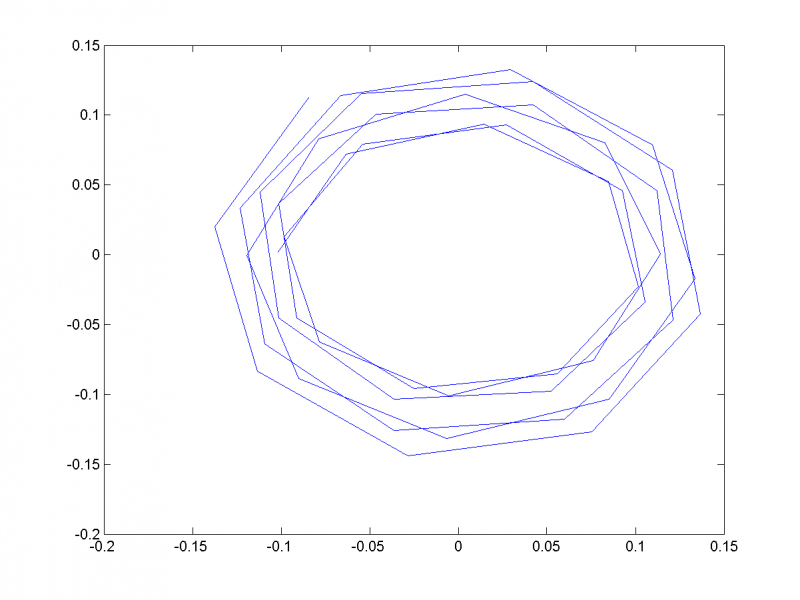
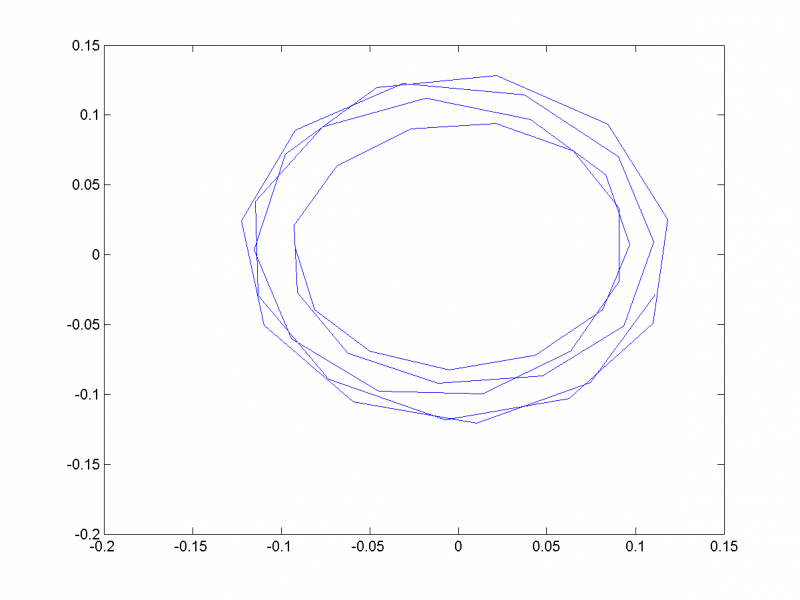
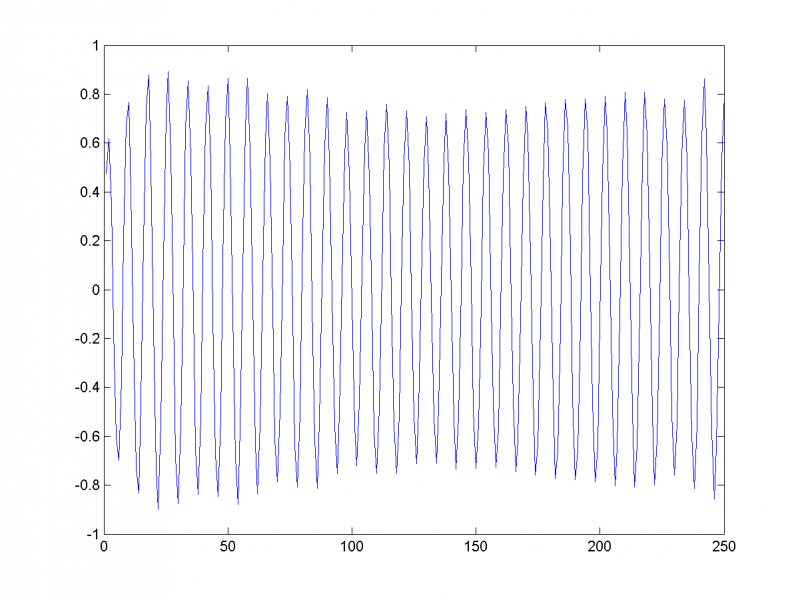
Обычно паре близких собственных чисел соответствуют главные компоненты, отвечающие одной частоте. Если отложить на одном графике главные векторы, отвечающие 3-му и 4-му собственным числам, становится очевидно, что они кореллируют и соответствуют периодической составляющей с периодом 11:

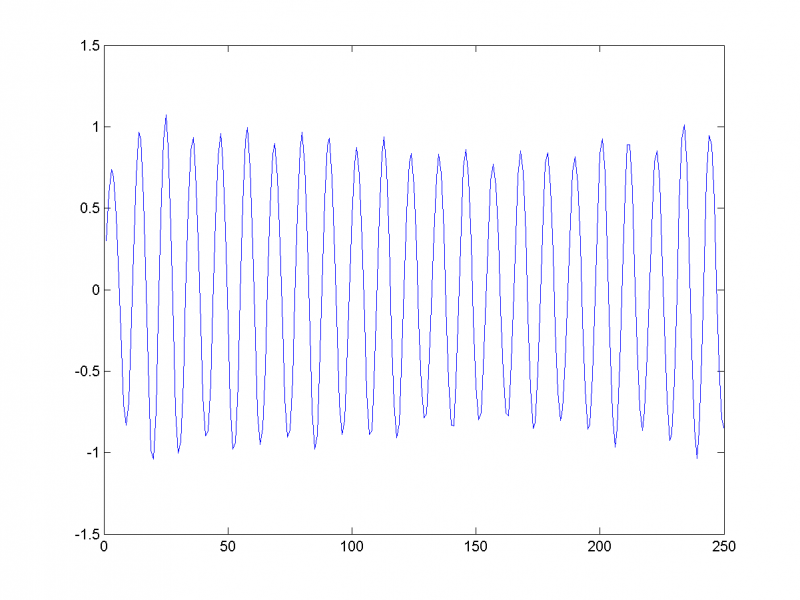
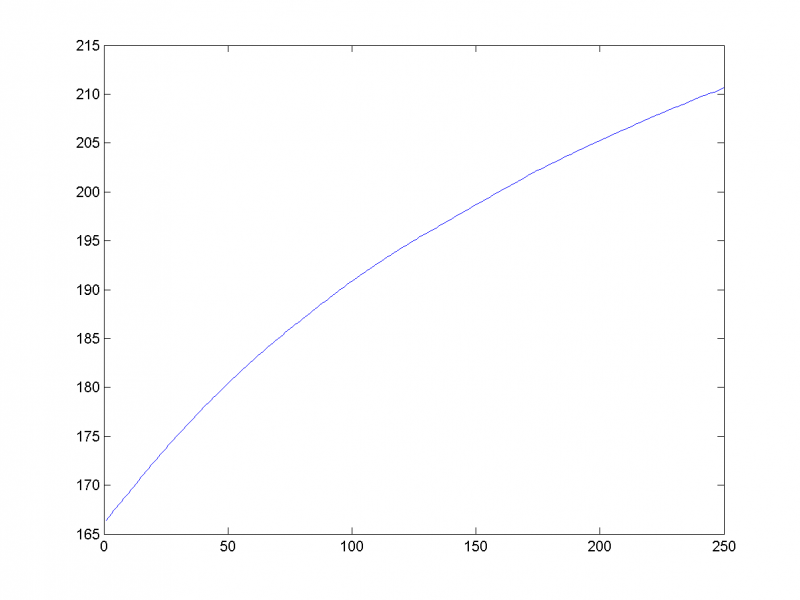
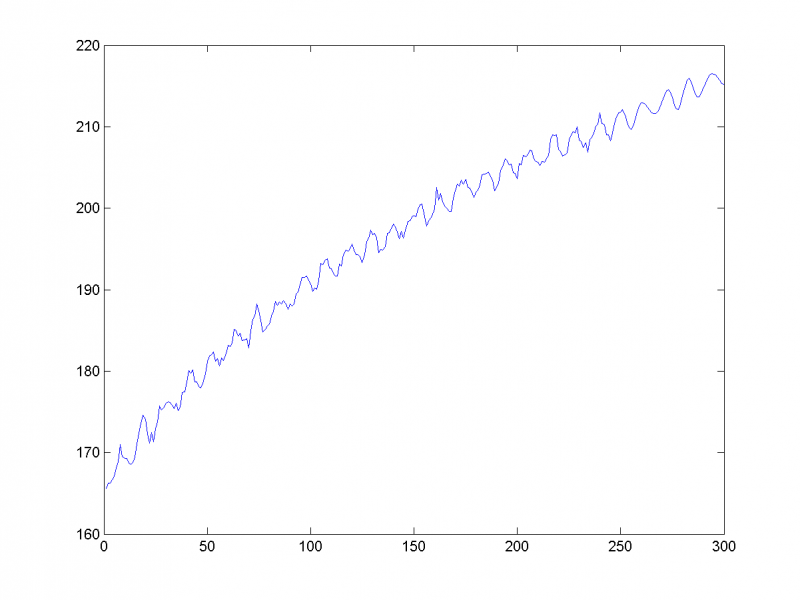
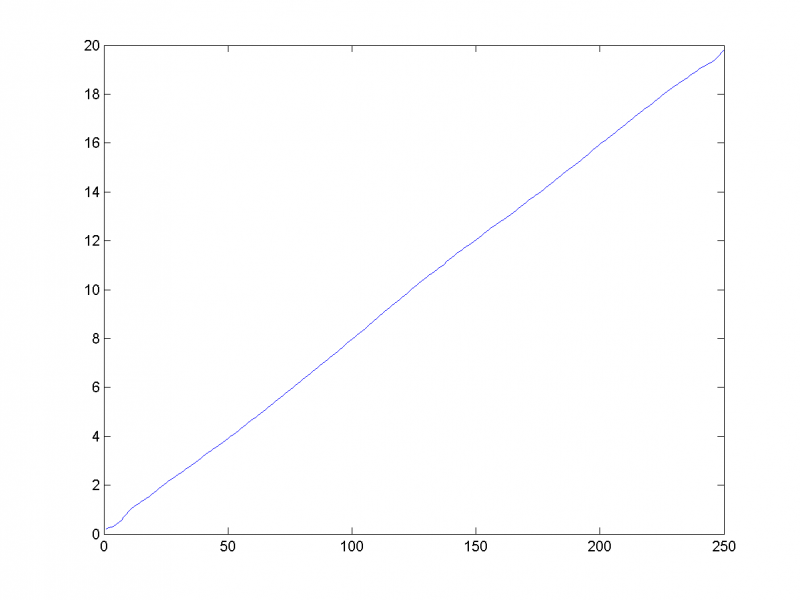
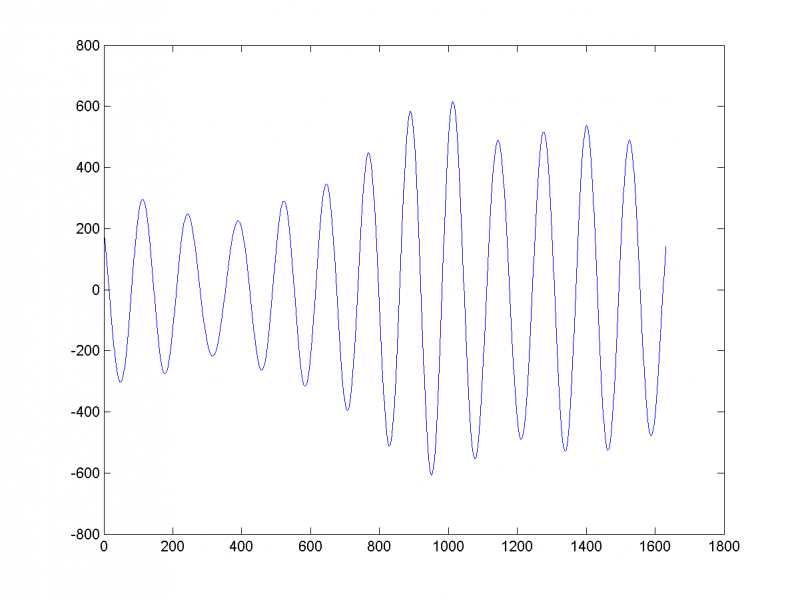
Восстановив временной ряд (на рисунке изображён первый из трёх) по этим двум главным компонентам, убеждаемся в этом:

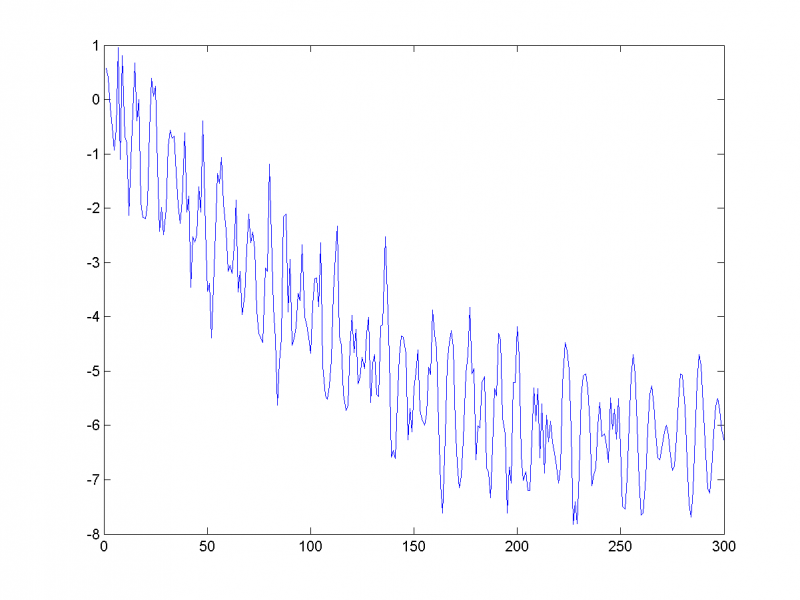
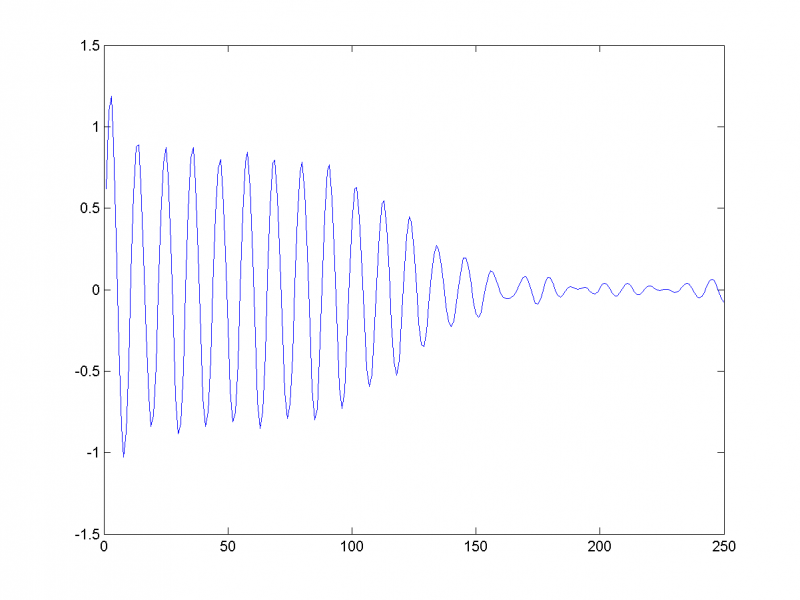
5-му и 6-му собственным числам соответствует периодическая составляющая с периодом 8:

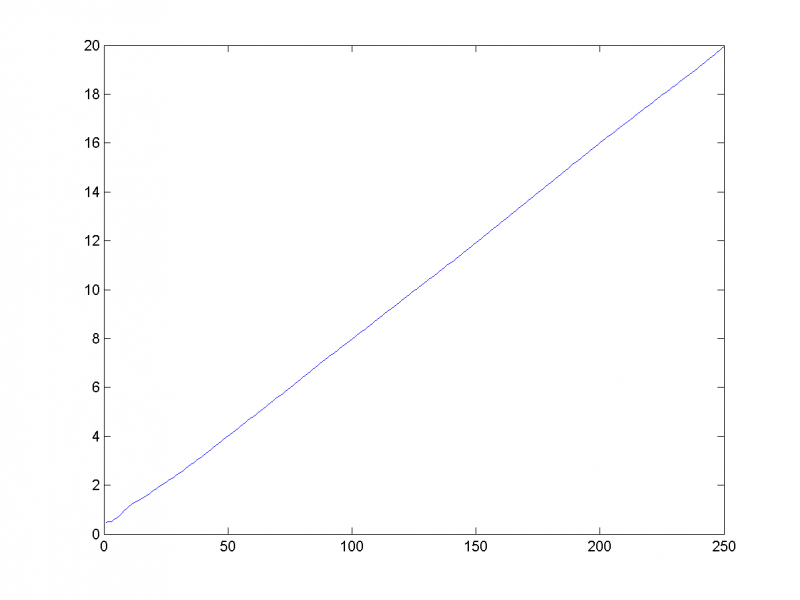
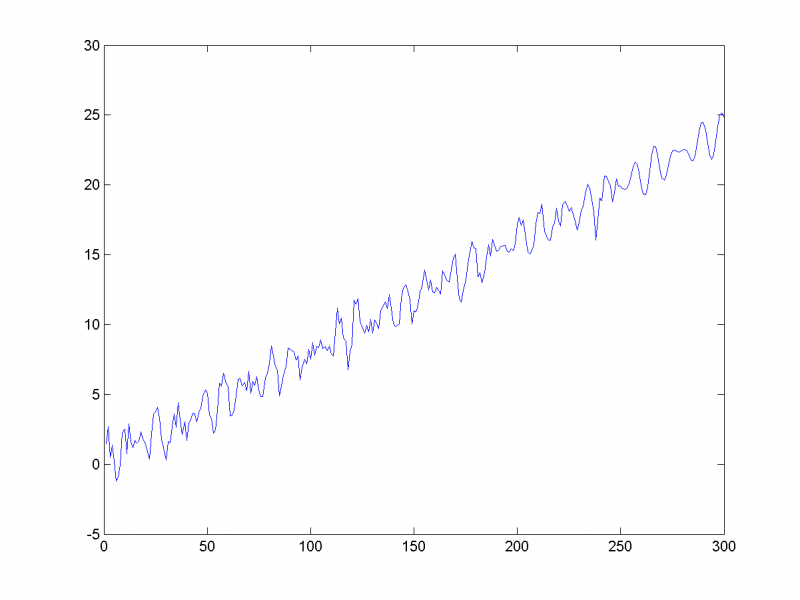
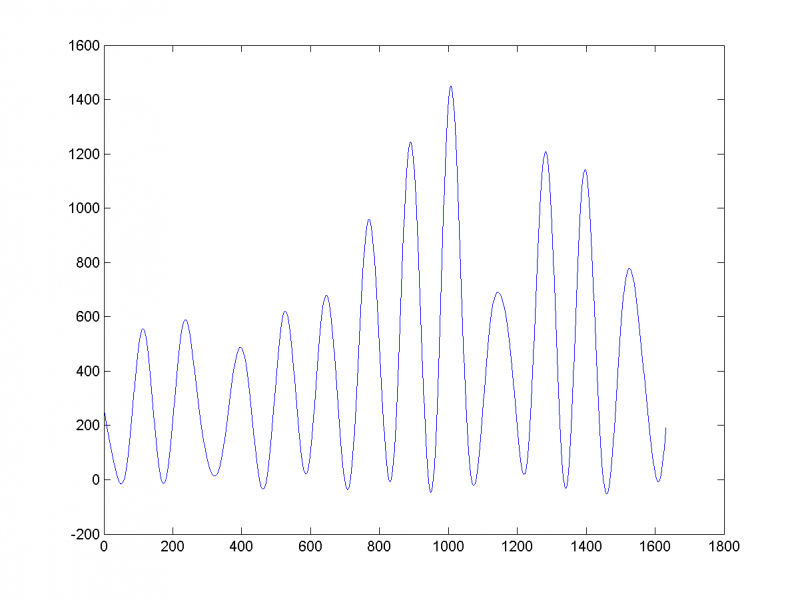
1-я, 2-я и 7-я главная компоненты отвечают за тренд:

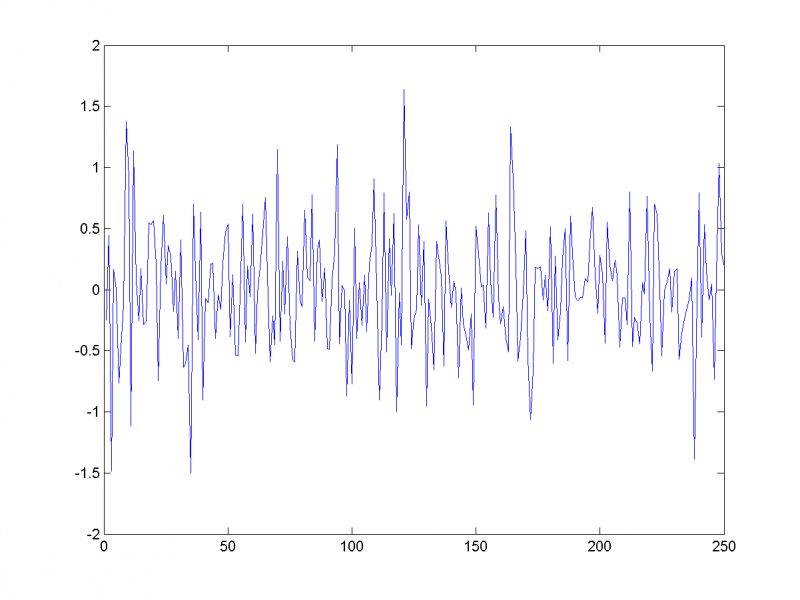
Убедимся, что остальные главные компоненты - это шум:

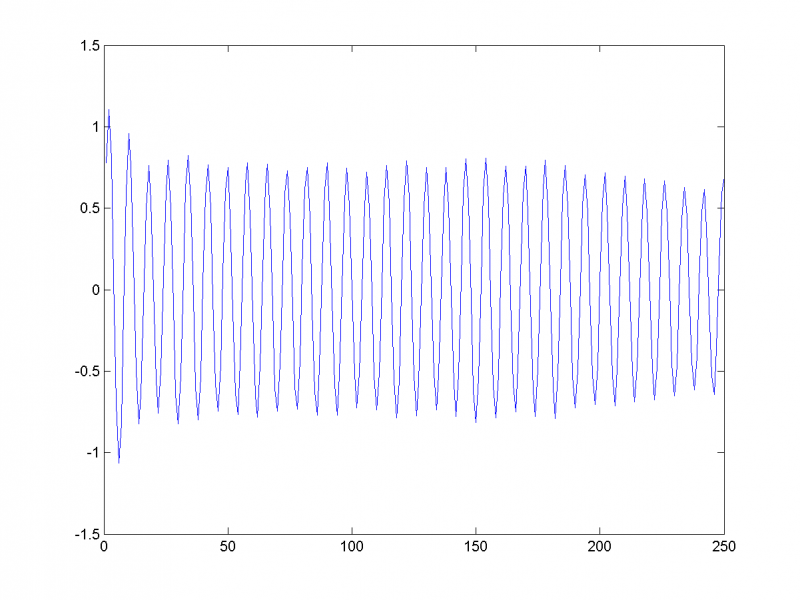
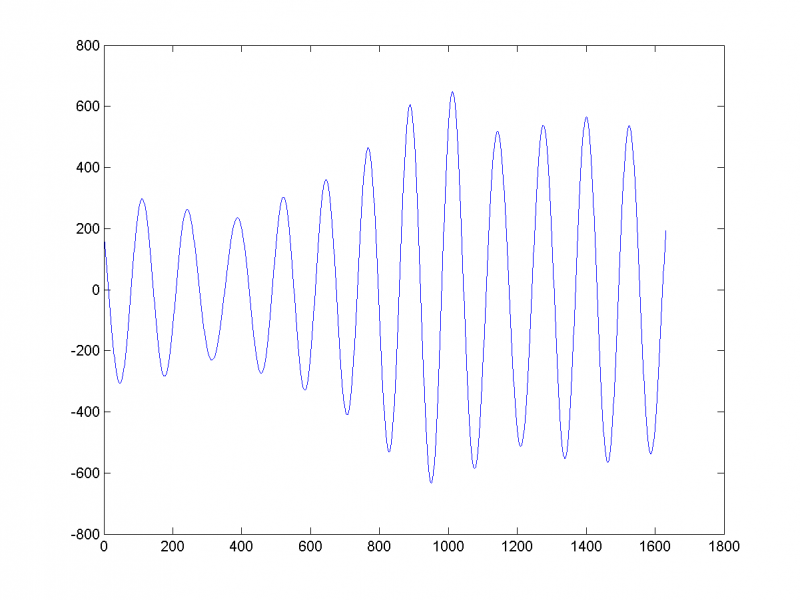
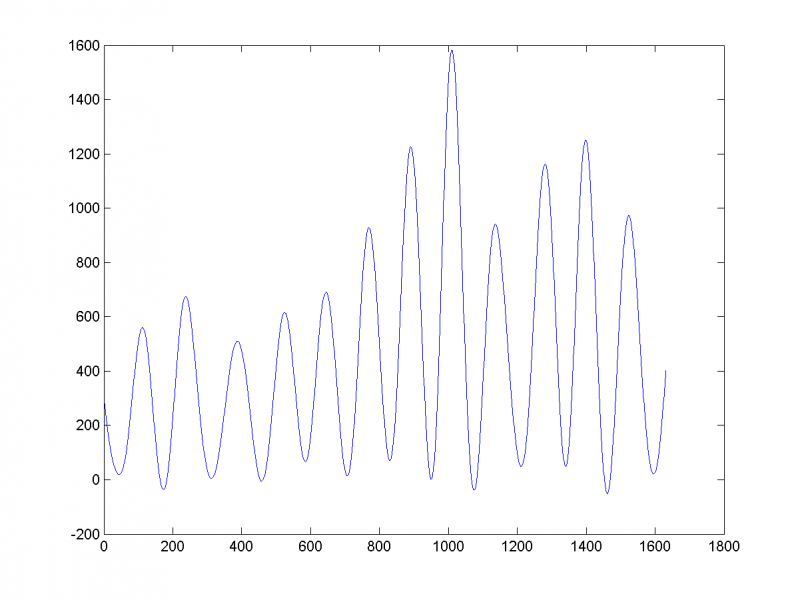
Спрогнозируем временной ряд на 50 единиц вперёд по первым семи главным компонентам:

Видим, что прогноз вполне адекватен.

Посмотрим, как отреагирует алгоритм на нарушение периодичности временного ряда. Во второй половине временного ряда изменим частоту, амплитуду и фазу одной из периодик:

$$f_1(t) = 0,08t + 0,6\sin (\frac{2\pi t}{14}) + 0,8\sin (\frac{2\pi (t+0,09)}{8})$$

$$f_2(t) = 0,0001t^2 - 0,05t + 0,45\sin (\frac{2\pi (t-0,14)}{14}) + \cos (\frac{2\pi t}{8})$$

$$f_3(t) = 36\log(t+100) - 0,8\sin (\frac{2\pi (t+0,24)}{14}) + 0,5\sin (\frac{2\pi (t-0,35)}{8})$$

$$t = 1, 2, \ldots, 250$$

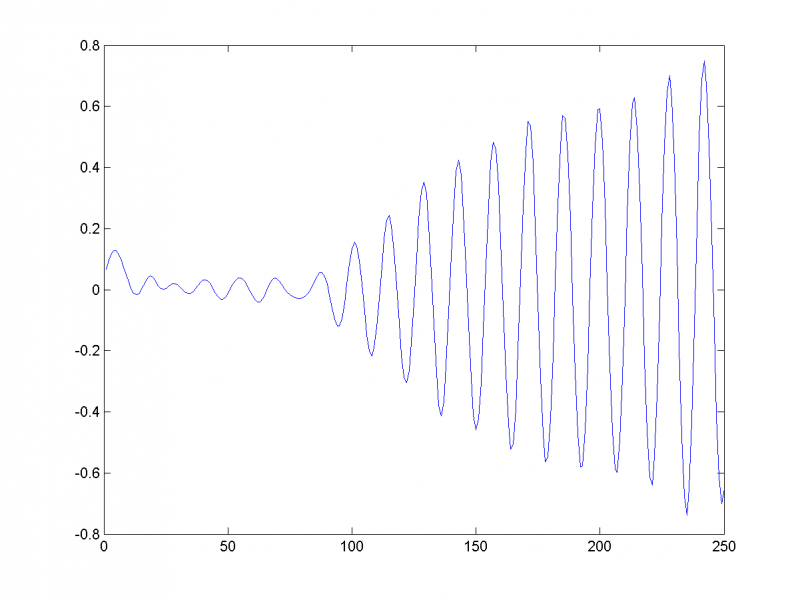
В этом случае 2-я и 3-я главная компонента будет соответствовать той периодике, которую мы не изменили: (все графики соответствуют первому временному ряду)

5-я и 6-я - первой половине изменённой компоненты:

7-я и 8-я - второй её половине:

1-я, 2-я и 9-я отвечают тренду:

Таким образом, алгоритм устойчив к нарушениям периодичности - разным участкам временного ряда соответствуют различные главные компоненты.

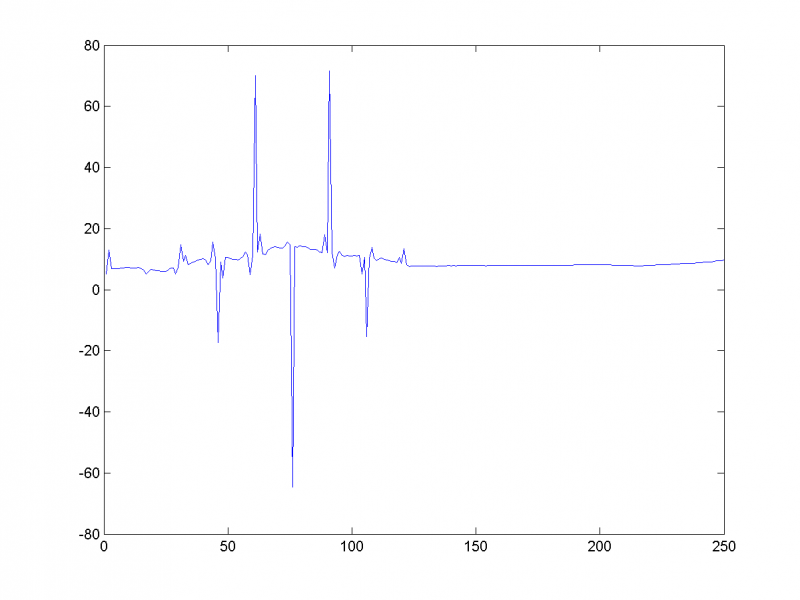
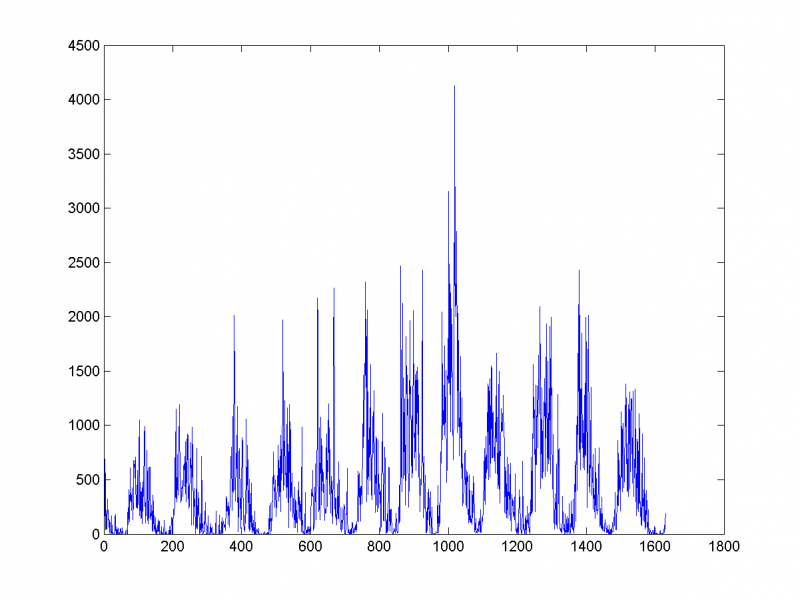
Посмотрим поведение алгоритма в случае наличия выбросов. Мы добавили выброс в среднем в каждую 50-ю точку временного ряда. Первое собственное число в этом случае на несколько порядков больше остальных, график логарифмов собственных чисел со 2-го по 20-е представлен ниже:

Восстанавливая ряд по первым 16-ти главным компонентам, видим, что алгоритм работает некорректно:

Реальные данные

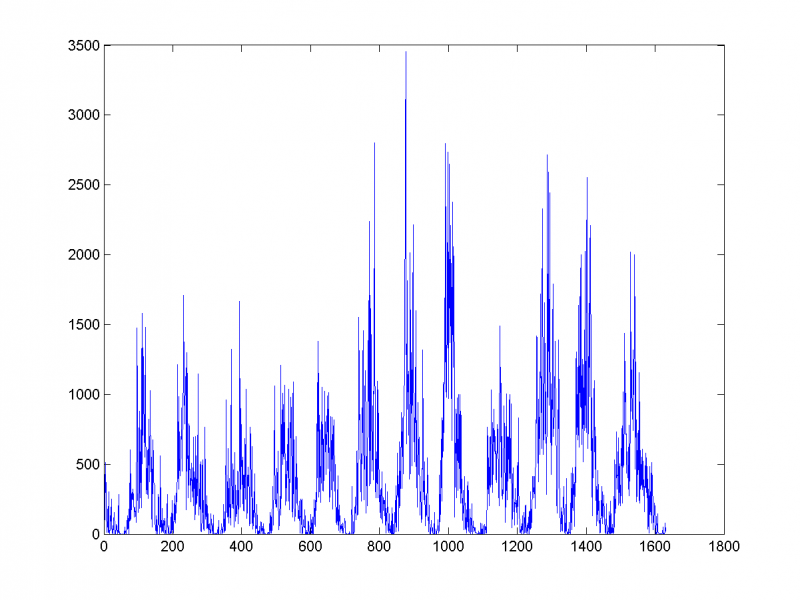
Рассмотрим ежемесячные данные о покрытии полушарий Солнца пятнами с 1876 года.

Южное полушарие:

Северное полушарие:

Используем гусеницу длины 250.

2-я и 3-я компоненты соответствуют 12-летним солнечным циклам:

Автор статьи не смог интерпретировать остальные главные компоненты. Однако субъективно первые шесть главных вполне адекватно характеризуют солнечную активность и могут быть использованы для прогноза:

См. также

Литература

  • Главные компоненты временных рядов:

метод "Гусеница"; под редакцией Д.Л.Данилова и А.А.Жиглявского

  • Analysis of Time Series Structure:

SSA and Related Techniques; Nina Golyandina, Vladimir Nekrutkin, Anatoly Zhigljavsky


Данная статья является непроверенным учебным заданием.
Студент: Участник:Илья Фадеев
Преподаватель: Участник:В.В.Стрижов
Срок: 28 мая 2010

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://poligon.machinelearning.ru/wiki/index.php?title=%D0%9F%D1%80%D0%BE%D0%B3%D0%BD%D0%BE%D0%B7%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5_%D0%B2%D1%80%D0%B5%D0%BC%D0%B5%D0%BD%D0%BD%D1%8B%D1%85_%D1%80%D1%8F%D0%B4%D0%BE%D0%B2_%D0%BC%D0%B5%D1%82%D0%BE%D0%B4%D0%BE%D0%BC_SSA_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»
Личные инструменты