Квадратичный дискриминант

Материал из MachineLearning.

(Различия между версиями)

Текущая версия

Квадратичный дискриминант - это вариант Байесовского классификатора, который основывается на двух дополнительных допущениях, касающихся вероятностных свойств выборки, а именно - независимость выборки и ее нормальность. Нормальное (гауссово) распределение широко используется по причине вычислительного удобства и адекватности во многих случаях.

Содержание

1 Постановка задачи
2 Основные допущения
3 Оценка параметров
4 Алгоритм классификации
- 4.1 Теорема
- 4.2 Доказательство
5 Недостатки
6 Литература

Постановка задачи

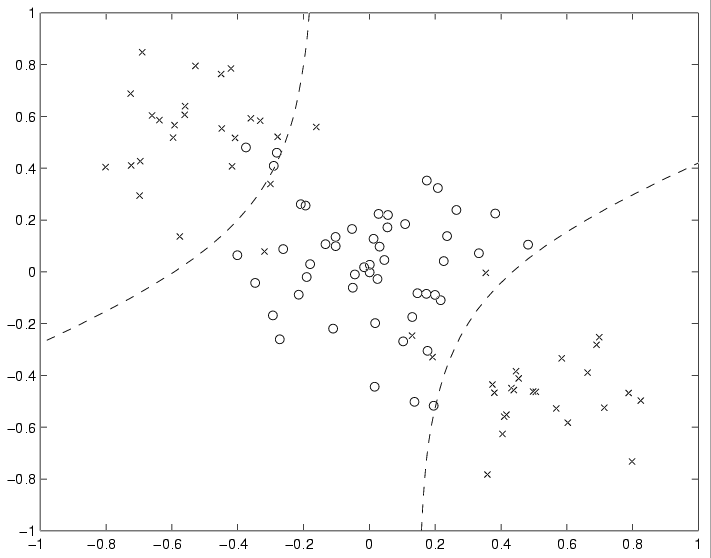
Необходимо построить классификатор, разделяющая поверхность которого имела бы квадратичный вид.

Основные допущения

Выборка независима, то есть

$p(x_1 ... x_m)=\prod_{i=1}^m p(x_i)$

Выборка имеет многомерное нормальное распределение. То есть функция правдоподобия имеет следующий вид:

$p(X)=N(X, \mu, \Sigma)=\frac {exp(-\frac {1}{2}(X- \mu)^T \Sigma^{-1} (X- \mu))}{\sqrt{(2 \pi)^n det \Sigma }}$

где $n -$ размерность пространства

Оценка параметров

Оценки, основанные на принципе максимума правдоподобия, принимают следующий вид для каждого класса $y$ :

$\hat \mu = \frac {1}{m} \sum _{i=1}^m x_i$

$\hat \Sigma = \frac {1}{m - det y} \sum _{i=1}^m (x_i-\hat \mu)(x_i-\hat \mu)^T$

Где $x_i \in y,$

$m -$ количество элементов в классе $y$

Алгоритм классификации

Пример разделяющей поверхности в двумерном случае

В общем виде, алгоритм Байесовского классификатора имеет вид

$a(x)=argmax_{y \in Y} \lambda_y p_y(x) P_y$

Иногда вместо самих вероятностей удобнее брать некоторые функции от них:

$g_y(x)=f(p_y(x))$

где $f -$ монотонно возрастает.

Функция $g_y(x)$ называется дискриминантной функцией, откуда и пошло название самого метода.

В условиях выдвинутых гипотез удобнее всего взять в качестве функции $f$ натуральный логарифм, и тогда алгоритм приобретает следующий вид:

$a(x)= argmax_{y \in Y} (ln \lambda_y P_y - \frac {1}{2}(x- \hat \mu_y)^T \Sigma^{-1} (x- \hat \mu_y) - \frac {1}{2} ln det {\hat \Sigma_y} )$

Теорема

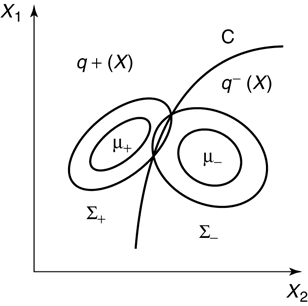
Квадратичный дискриминант имеет квадратичную разделяющую поверхность, которая вырождается в линейную, если ковариационные матрицы классов совпадают.

Доказательство

Поверхность, разделяющая классы $s$ и $t$ , описывается уравнением

$\lambda_s P_s p_s(x)=\lambda_t P_t p_t(x)$

После логарифмирования

$ln p_s(x)-ln p_t(x)=C_{st}$

где $C_{st}=ln(\lambda_s P_s /\lambda_t P_t) -$ константа, не зависящая от $x$ . Разделяющая поверхность в общем случае квадратична, так как $ln p_y(x)$ является квадратичной формой по $x$ .

$ln p_y(x)=-\frac {n}{2} ln 2\pi -\frac{1}{2} ln det {\Sigma_y} -\frac{1}{2}(x-\mu_y)^T \Sigma_y^{-1} (x-\mu_y)$

Если $\Sigma_s=\Sigma_t$ , то квадратичные члены сокращаются и уравнение разделяющей поверхности вырождается в линейную форму:

$(x-\mu_{st})^T \Sigma_y^{-1} (\mu_s-\mu_t)=C_{st}$

где $\mu_{st}=\frac{1}{2}(\mu_s+\mu_t) -$ точка посередине между центрами классов.

Имеет ли смысл описывать геометрию разделяющих поверхностей здесь, или лучше оформить это отдельной статьей?

Недостатки

Пример гиперболической разделяющей поверхности в двумерном случае

Если длина выборки меньше размерности пространства, $l_y < n$ , то матрица $\hat\Sigma_y^$ становится вырожденной, так как ее ранг не может превышать $l_y$ . В этом случае обратная матрица не существует, и метод неприменим.

Даже если длина выборки достаточно велика, матрица $\hat\Sigma_y^$ все равно может оказаться вырожденной. Это происходит, когда некоторые признаки линейно зависимы. Это так называемая проблема мультиколлинеарности. Более того, признаки могут быть почти линейно зависимы. В этом случае матрица $\hat\Sigma_y^$ будет близка к вырожденной, иначе говоря, плохо обусловлена. Такие матрицы обладают рядом неприятных свойств, например при их обращении получаются неустойчивые решения. Положение разделяющей поверхности может сильно непредсказуемо меняться при незначительной вариации обучающих данных.

Выборочные оценки чувствительны к нарушениям нормальности распределений, в частности, к редким большим выбросам. Мат.ожидание в таком случае значительно смещается. При увеличении размерности влияние загрязнений только усиливается.

Если функции правдоподобия классов существенно отличаются от гауссовских, то метод квадратичного дискриминанта будет приводить к алгоритмам низкого качества. Например, когда имеются признаки, принимающие дискретные значения, или когда классы распадаются на изолированные сгустки.

Литература

К.В.Воронцов „Лекции по статистическим (байесовским) алгоритмам классификации“
Л.М.Местецкий Курс лекций "Математические методы распознавания образов"

Данная статья является непроверенным учебным заданием.

Студент: Участник:Вера Батурина

Преподаватель: Участник:Константин Воронцов

Срок: 6 января 2010

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://poligon.machinelearning.ru/wiki/index.php?title=%D0%9A%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82%D0%B8%D1%87%D0%BD%D1%8B%D0%B9_%D0%B4%D0%B8%D1%81%D0%BA%D1%80%D0%B8%D0%BC%D0%B8%D0%BD%D0%B0%D0%BD%D1%82»

Категории: Непроверенные учебные задания | Байесовская теория классификации

@@ Строка 24: / Строка 24: @@
 ::<tex>\hat \mu = \frac {1}{m} \sum _{i=1}^m x_i</tex>
-::<tex>\hat \Sigma = \frac {1}{m} \sum _{i=1}^m (x_i-\hat \mu)(x_i-\hat \mu)^T</tex>
+::<tex>\hat \Sigma = \frac {1}{m - det y} \sum _{i=1}^m (x_i-\hat \mu)(x_i-\hat \mu)^T</tex>
 Где <tex>x_i \in y,</tex>
@@ Строка 92: / Строка 92: @@
 {{Задание|Вера Батурина|Константин Воронцов|6 января 2010}}
-[[Категория:Непроверенные учебные задания]]
+[[Категория:Байесовская теория классификации]]